A tiny ball of mass m is released from the state of rest over a large smooth sphere of mass M and radius R, which is at rest on a smooth horizontal surface. If the ball strikes the sphere perfectly inelastically, find their velocities after collision.
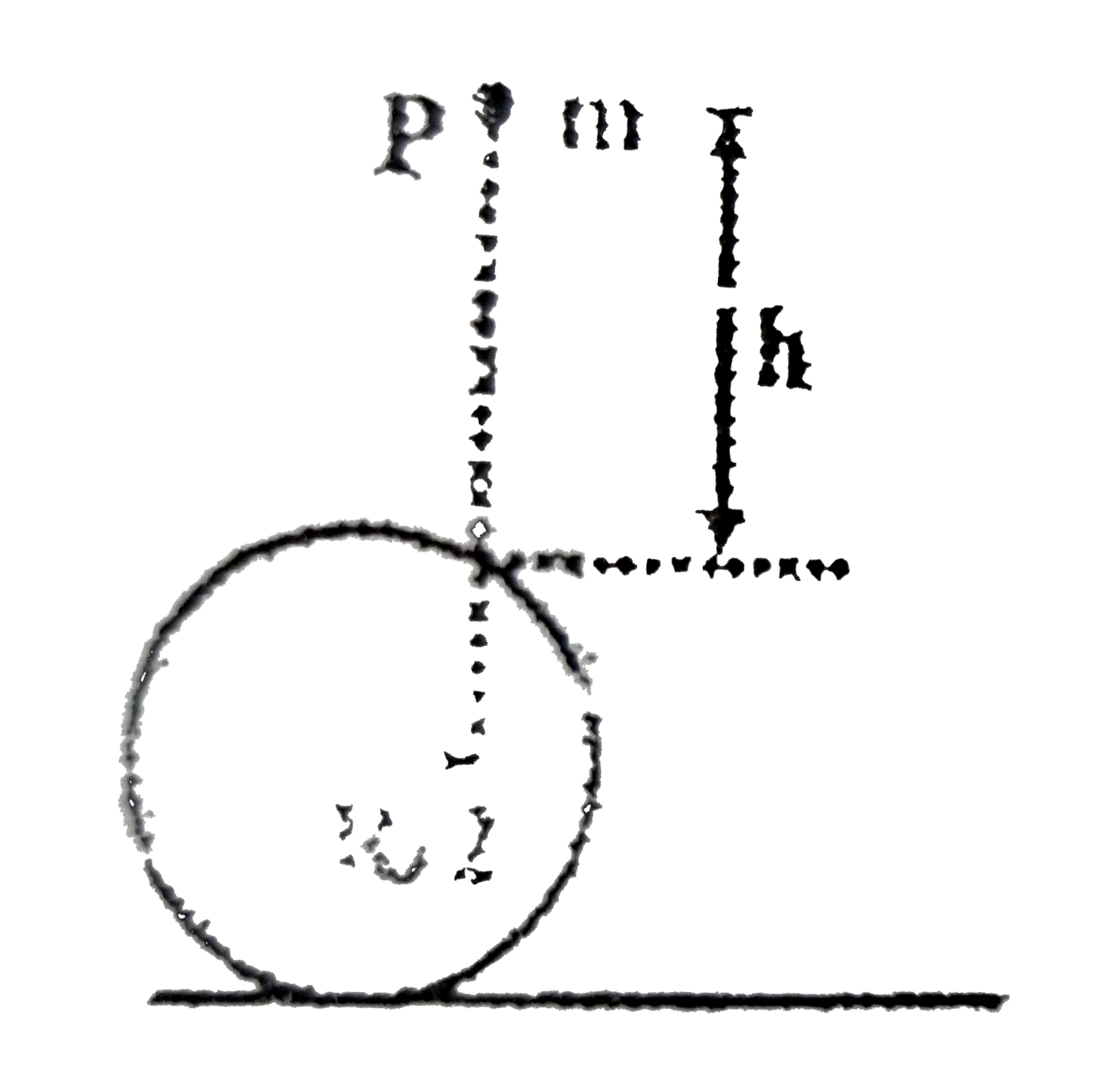
Velocity attained by ball just before it strikes the surface
u=√2gh
∴Sinθ=R/2R⇒θ=30∘
After collision let the velocity of the sphere be V and the components of velocity of ball along common normal OL and along common tangent be va and vt respectively.
In the absence of external force in the horizontal direction, the linear momentum conserved.
0+0=−MV+mvnsinθ+mvtcosθ (1)
Along the common normal at ,
Vsinθ−(−vn)=e[ucosθ−0](2)
e=0 for inelastic collision.
∴Vsinθ=−vn
∴vn=−v/2 (3)
Along the common tangent velocity components before and after collision remain same.
∴usinθ=v1⇒vt=u2 (4)
Using (3) and (4) in (1),
MV=m(−V2)12+m(u2)√32
(M+m2)V=mu√34
Velocity of sphere V=m√6gh2(2M+m)∵u=√2gh
Velocity of ball v=√v2n+v2t=
⎷6ghm24(2M+m)2+gh2

Topper's Solved these Questions
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
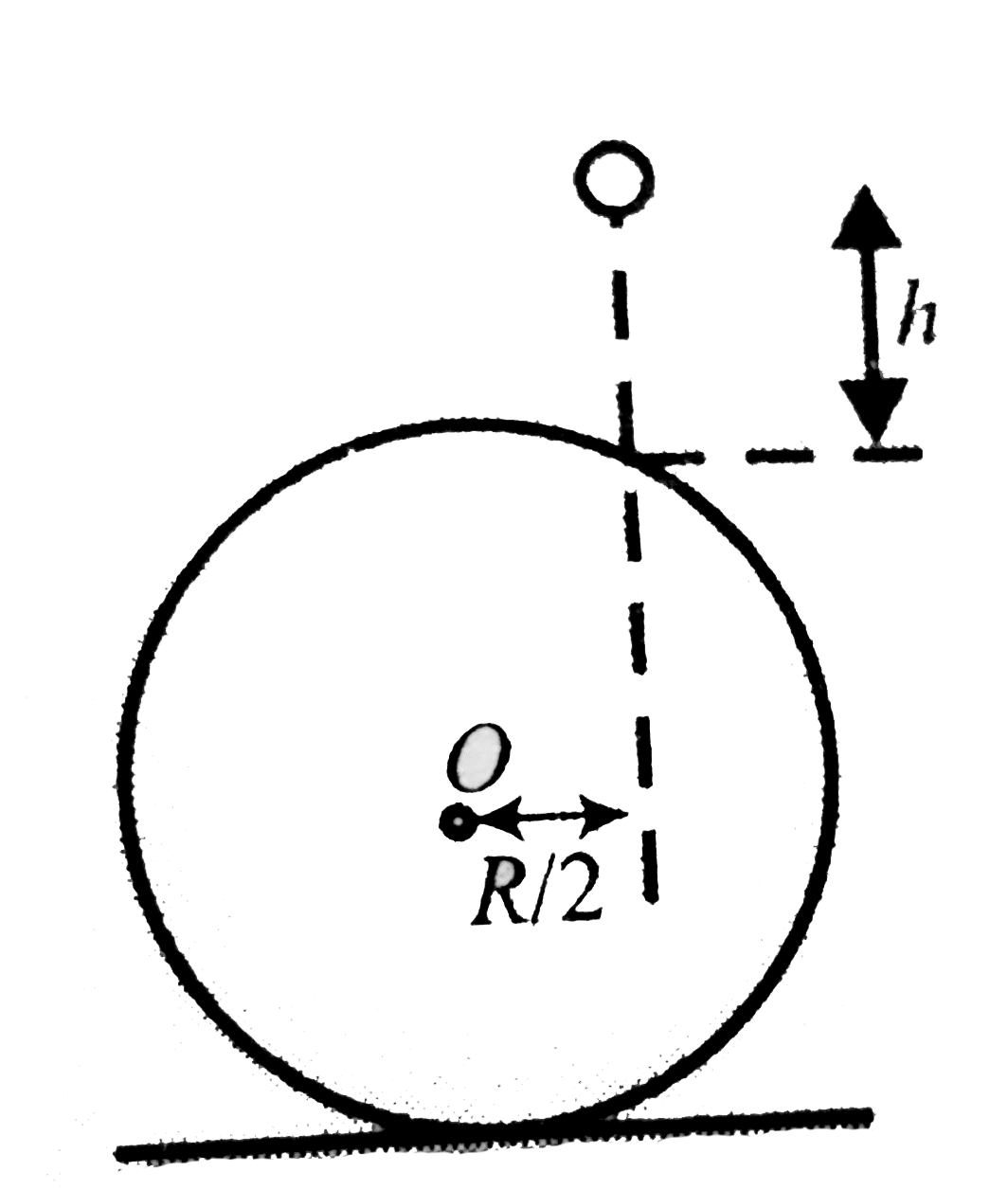
View Solution
Knowledge Check
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A bullet of mass m is fired horizontally into a large sphere of mass M and radius R resting on a smooth horizontal table.

The bullet hits the sphere at a height h from the table and sticks to its surface. If the sphere starts rolling without slippng immediately on impact, thenAhR=4m+3M2(m+M)BhR=m+3Mm+2MChR=10m+7M5(m+M)DhR=4m+3Mm+MA small ball ( uniform solid sphere ) of mass m is released from the top of a wedge of the same mass m. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.
The total kinetic energy of the ball just before it falls on the groundA2mghBmghC1318mghDNone of these
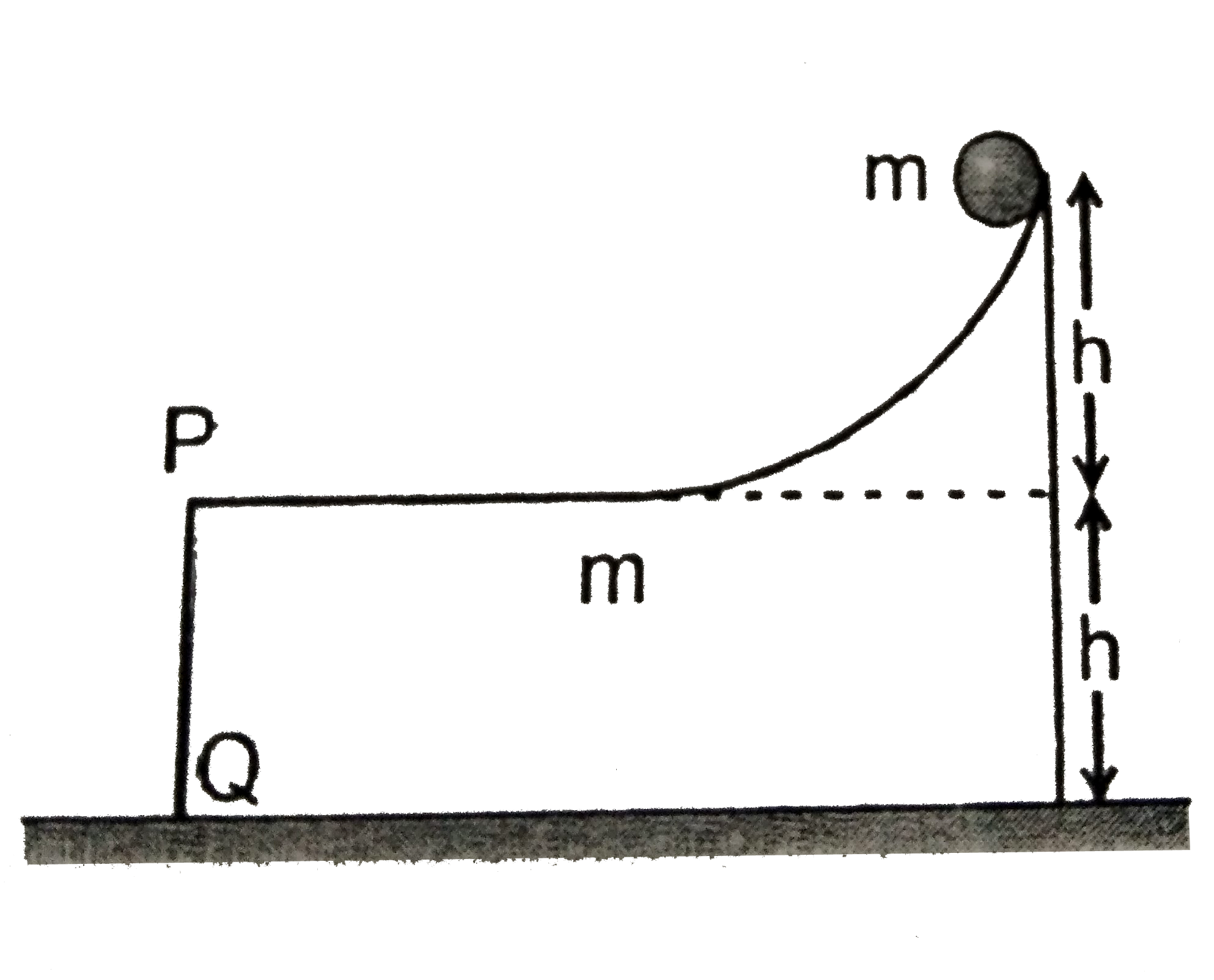
A particle (a mud pallet, say) of mass m strikes a smooth stationary wedge of mass M with as velocity v0 at an angle θ with horizontal. If the collision is perfectly inelastic, find the
a. velocity of the wedge just after the collision.
b. Chane in KE of the system (M+m) in collision.
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionTwo equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on them and reduces to rest. Then:

View Solution

