A uniform thin flat isolated disc is floating in spece. It has radius R and mass m. A force F is applied to it a distanced =R2 from the centre in the y-direction Treat this problem as two-dimensional. At the instant shown the:
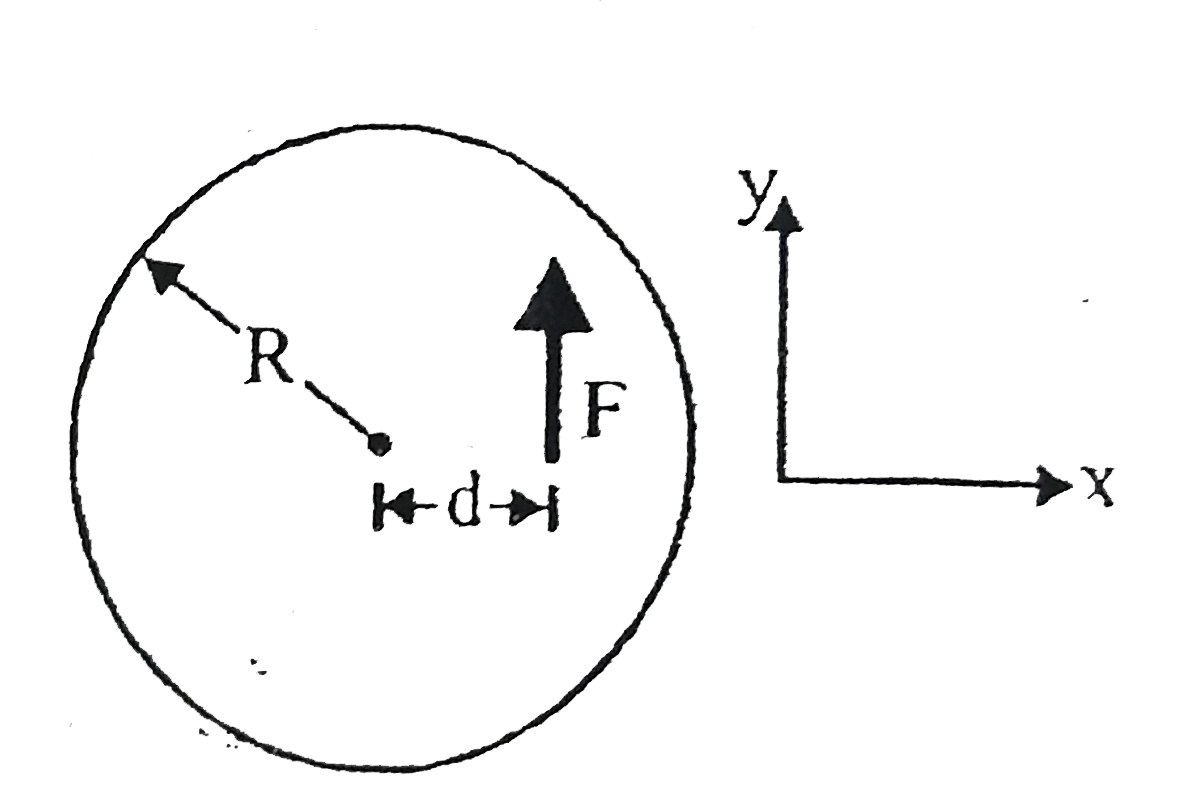
acceleration of the centre of the disc is f/m
angular acceleration of the disk is F/mR
acceleration of leftmost point on the disc is zero
Point which is instantaneously unaccelerated is the rightmost point.
The correct Answer is:A, B, C
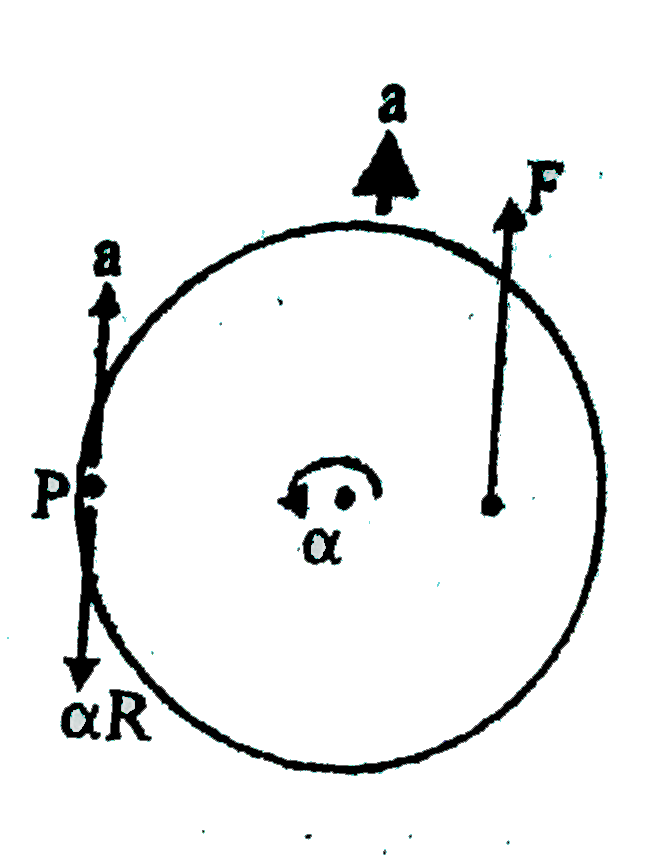
F=ma……(1)
FR2=12mR2α…..(2)
aP=a−αR=0
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective
107 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
In a given system of unit standard measurement of mass is 100 gm standard measurement of length is 200 cm and standard measurement of time is 5 sec 10 J energy in the given system of unit has value N, then value of N is
View SolutionThe manifestation of band structure in solids is due to
View SolutionStatement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
View SolutionGiven a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA uniform thin flat isolated disc is floating in space. It has radius R and mass m . A force is applied to it at a distance d=(R2) from the centre in the y-direction. Treat this problem as two-dimensional. Just after the force is applied:
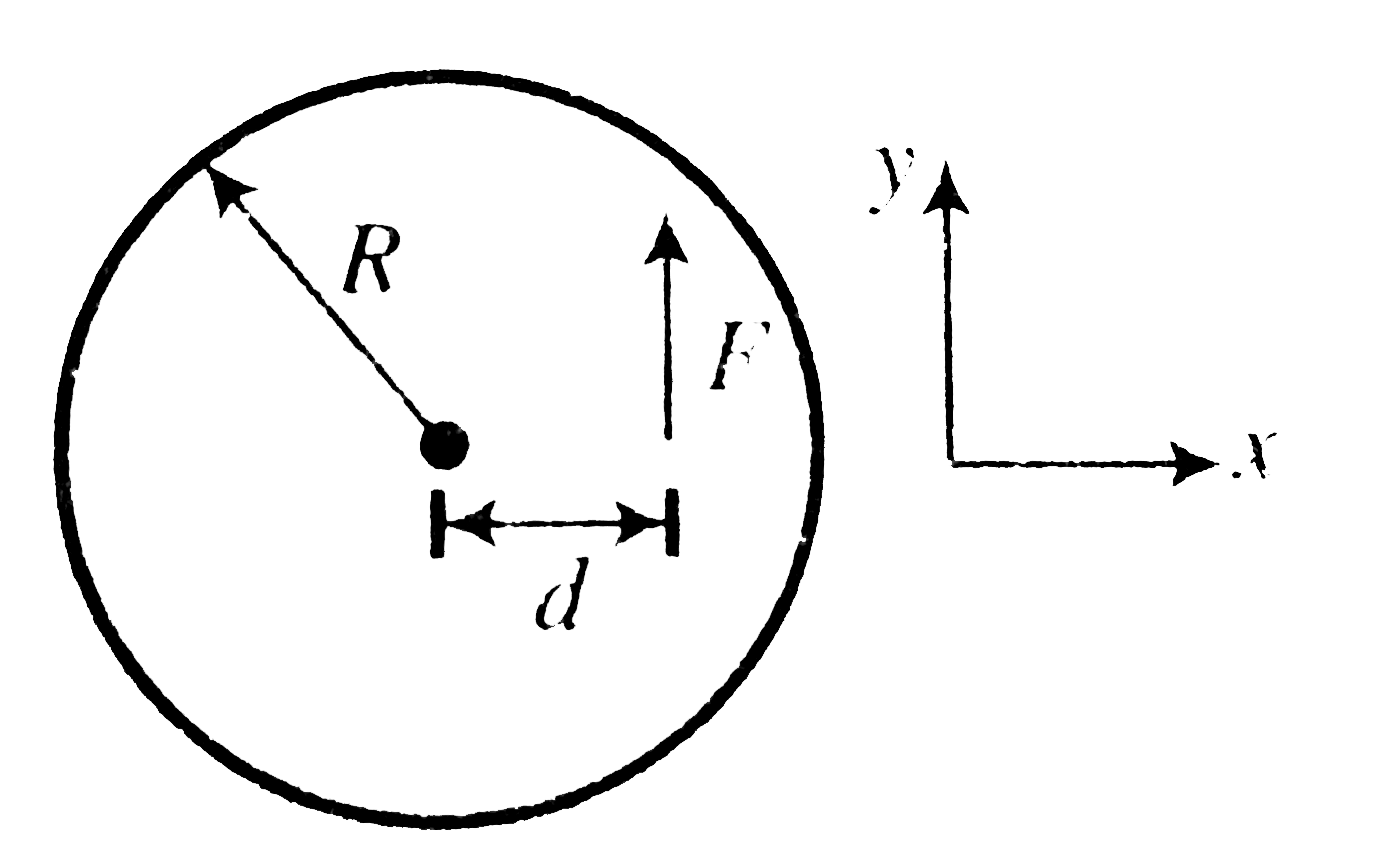
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
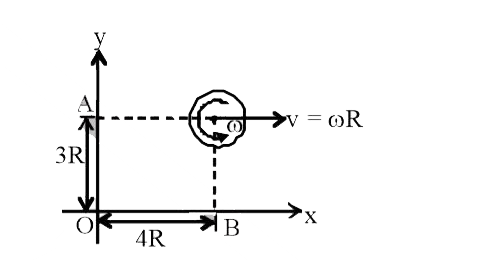
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
View SolutionA uniform disc of radius R has a hole cut out which has a radius r. The centre of hole is at a distance (R )/(2) from the centre of disc. The position of centre of mass is :
View SolutionFrom a uniform disc of radius R, a circular disc of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of original disc. Locate the centre of gravity of the resultant flat body.
View Solution
