A uniform thin flat isolated disc is floating in space. It has radius R and mass m . A force is applied to it at a distance d=(R2) from the centre in the y-direction. Treat this problem as two-dimensional. Just after the force is applied:
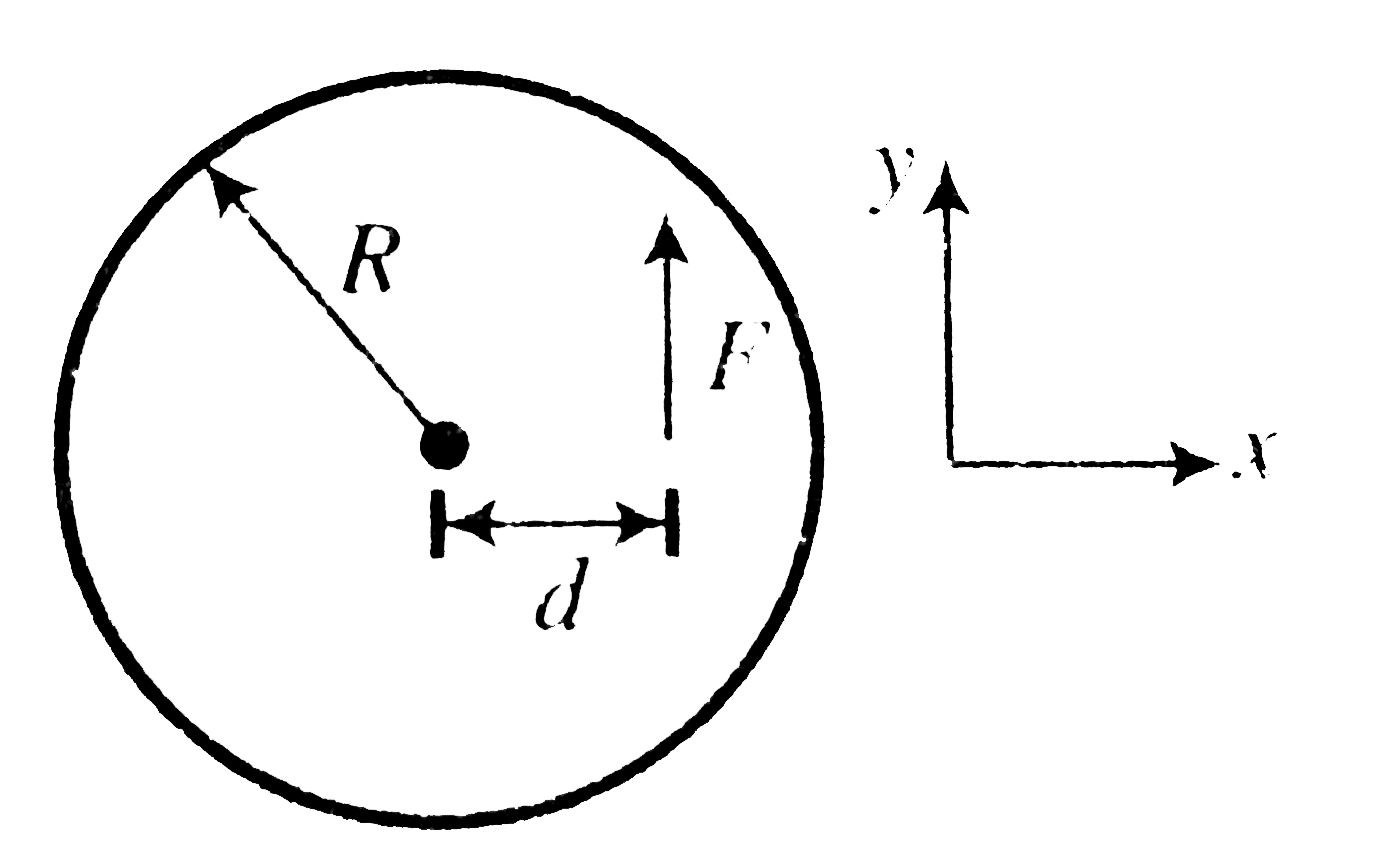
acceleration of the centre of the disc is F/m.
angular acceleration of the disk is F/mR.
acceleration of leftmost point on the, disc is zero
point which is instantaneously unaccelerated is the rightmost point.
The correct Answer is:A, B, C
F=ma……….i

FR2=12mR2α…………ii
aP=a−αR=0
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Single Correct
Explore 97 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
The mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
Knowledge Check
A uniform thin flat isolated disc is floating in spece. It has radius R and mass m. A force F is applied to it a distanced =R2 from the centre in the y-direction Treat this problem as two-dimensional. At the instant shown the:
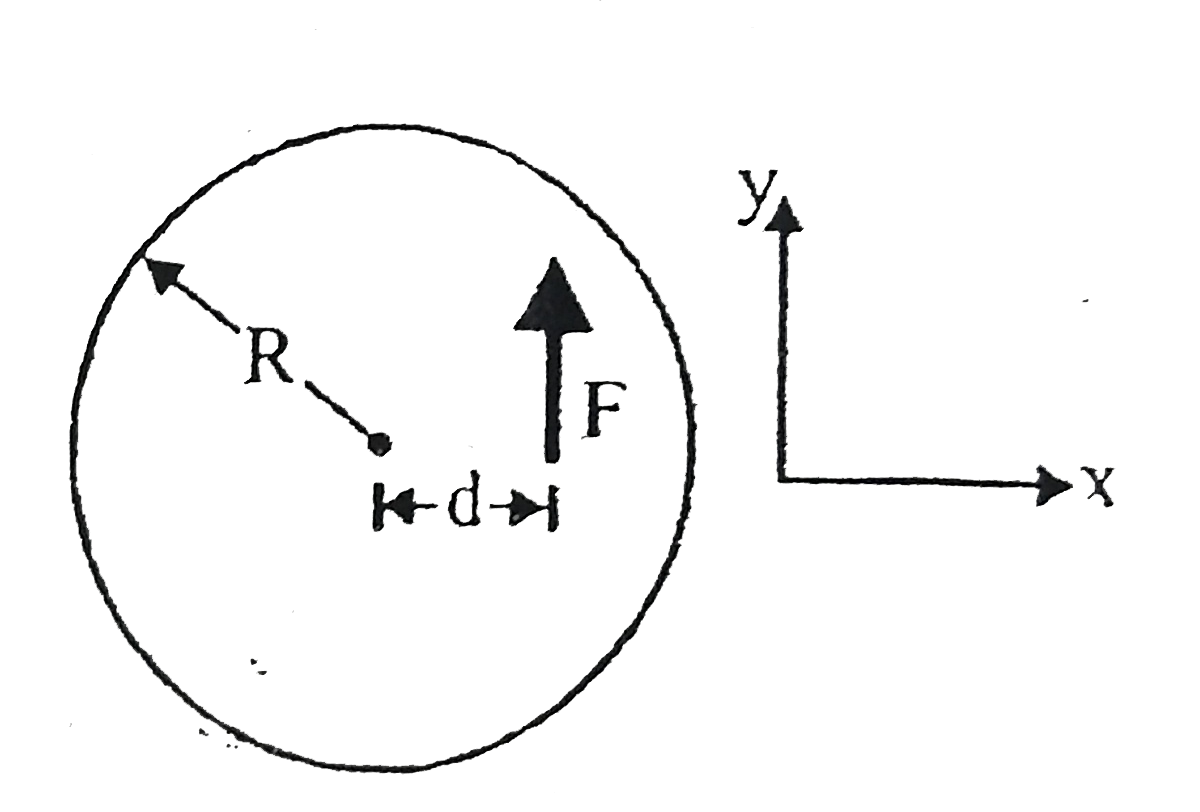 Aacceleration of the centre of the disc is f/mBangular acceleration of the disk is F/mRCacceleration of leftmost point on the disc is zeroDPoint which is instantaneously unaccelerated is the rightmost point.
Aacceleration of the centre of the disc is f/mBangular acceleration of the disk is F/mRCacceleration of leftmost point on the disc is zeroDPoint which is instantaneously unaccelerated is the rightmost point.Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
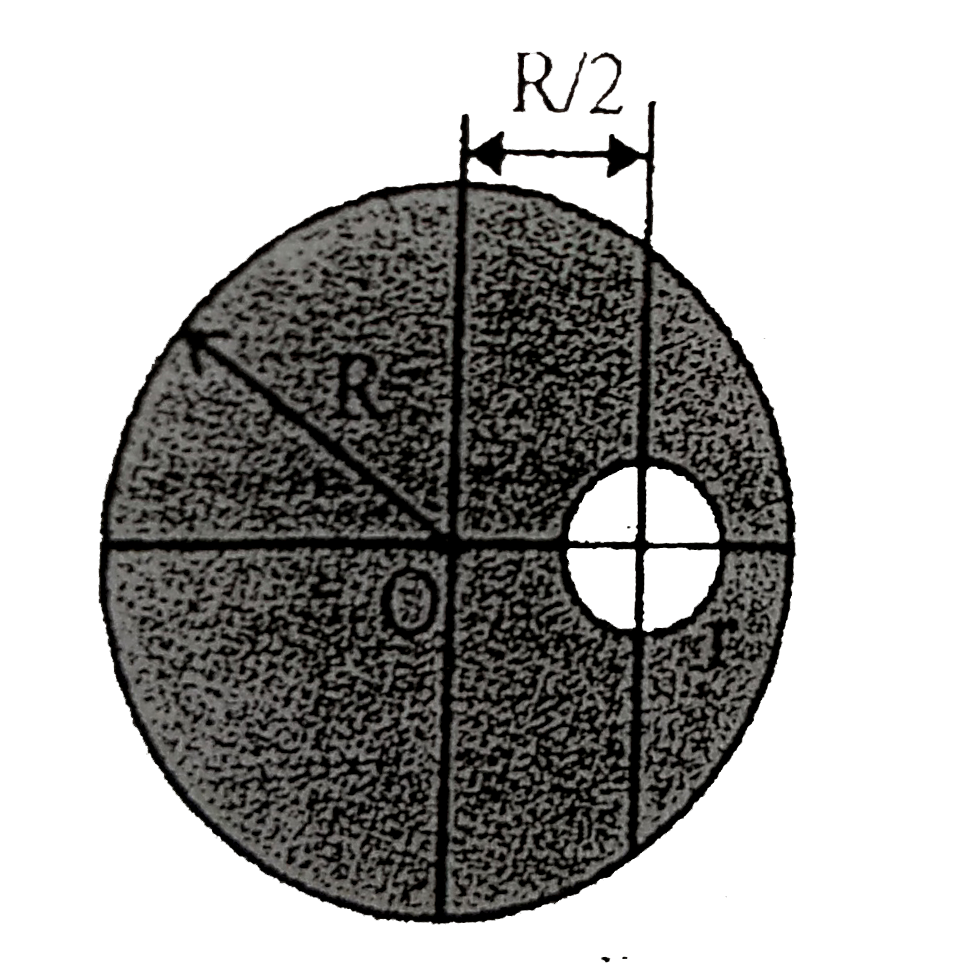 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBFCF(L−y)LDF(l−y)M
From a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
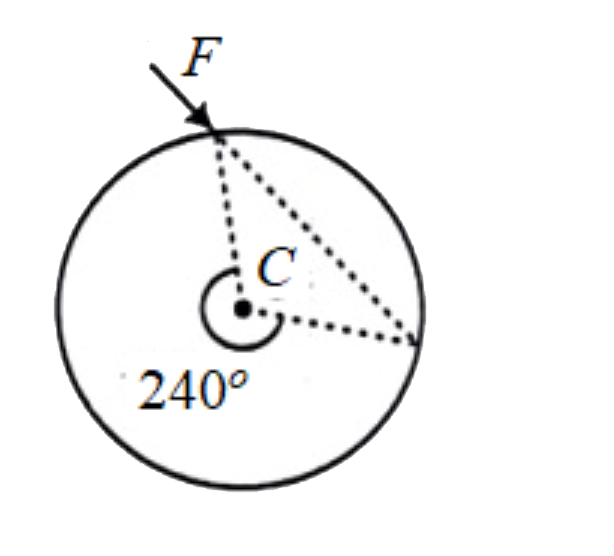
View SolutionA shell of mass M and radius R has another point mass m placed at a distance r from its centre (r>R). The force of attraction between the shell and point mass is :
View SolutionA body of mass 1 kg is moving towards east with a uniform speed of 2m/s. A force of 2N is applied to it towards north. The magnitude of the displacement of the body 2s after the force is applied is
View Solution
