Three coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

2√2D7
√(17)D8
4√5D
4√2D7
The correct Answer is:B

for nearest minima
dsinθ=8λ/3(i.e.2λ/3+λ+λ)⇒3λsinθ=8λ/3⇒sinθ=8/9
⇒tanθ=D/x=8√17⇒x=√(17)D8
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
The velocity- time graph of car moving on a straight track is given below. The car weight 1000kg.
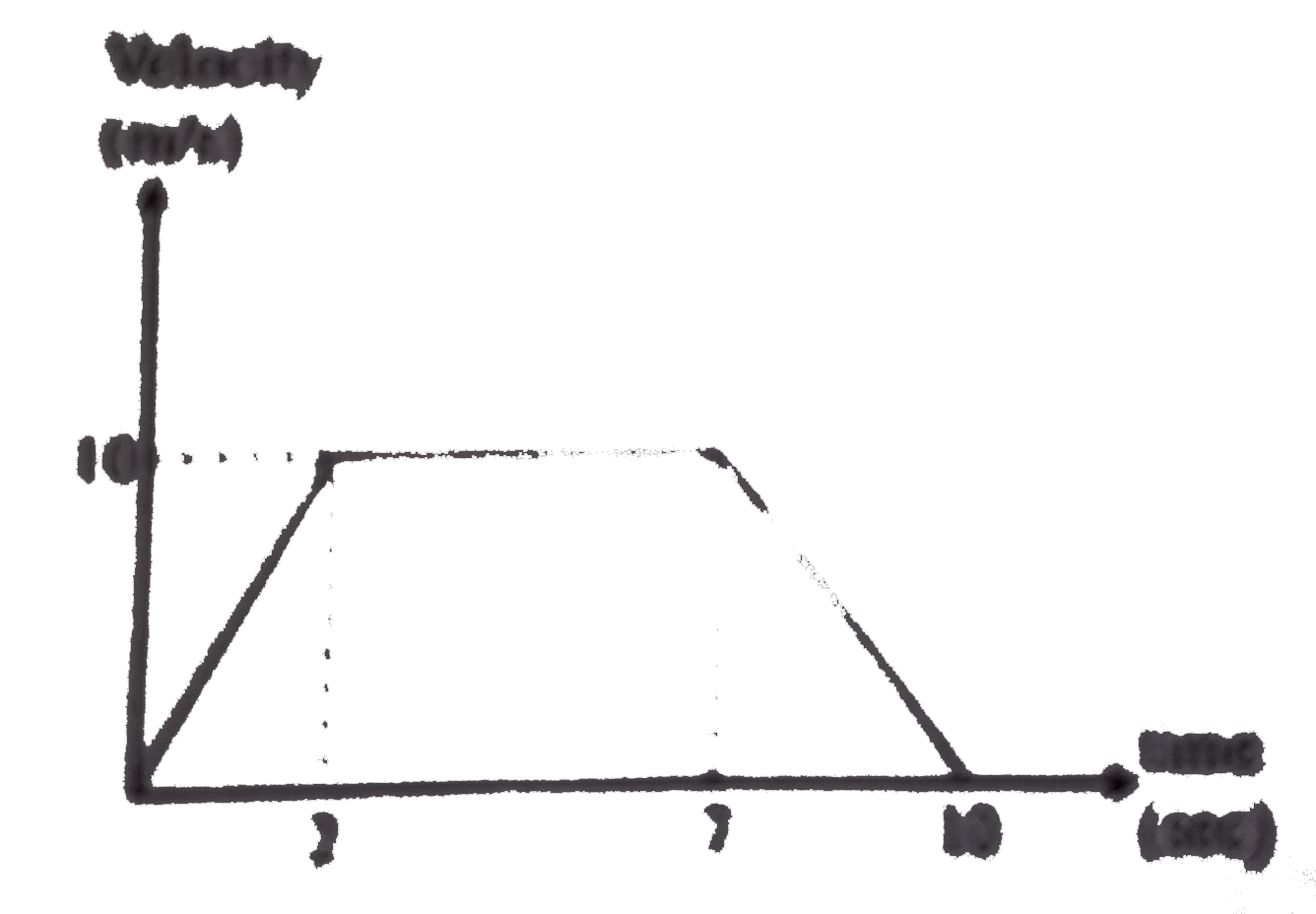 The distance travelled by the car during the whole motion is:
The distance travelled by the car during the whole motion is:
View SolutionStatement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
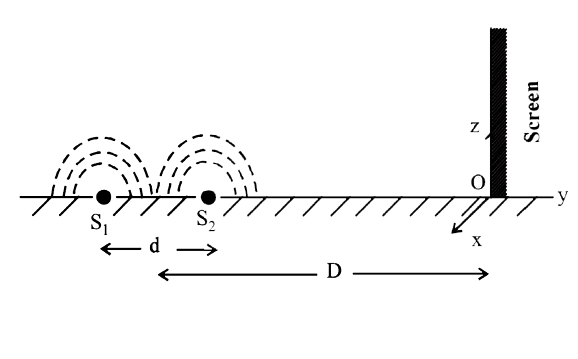
View SolutionWhile conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1,S2) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (forz>0) at a distance D=3 m from the mid-point of S1,S2, as shown schematically in the figure. The distance between the sources d=0.6003mm. The origin O is at the intersection of the screen and the line joining S1S2. Which of the following is (are) true of the intensity pattern of the screen?
View SolutionTwo monochromatic coherent point sources S_(1) and S_(2) are separated by a distance L. Each sources emits light of wavelength lambda , where L gt gt lambda . The line S_(1) S_(2) when extended meets a screen perpendicular to it at point A. Then
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionA monochromatic point source (S_(1)) is at a distance d from a screen. Another identical source (S_(2)) is at a large distance from the screen. The two sources are on a line which is perpendicular to the screen. Sources are coherent. What is the shape of interference fringes on the screen? (b) Three identical coherent sources are placed on a straight line with two neighbouring ones separated by a distance "d = 0.06 mm" . The sources produce monochromatic light of wavelength lambda" = 550.4 nm" . A line AB is located at a distance D = 2.50 m from the sources and is perpendicular to line joining the three sources. Intensity of light at P with any one of the sources switched on is I_(o) . Find the intensity when all three sources are switched on. Distance of point P from O is "y = 1.72 cm (see figure)"
View SolutionThree coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda .The separation between the sources is 2 lambda .The smallest distance from S_(2) on a line passing through S_(2) and perpendicular to S_(1)S_(2) where a minimum intensity occurs is :
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
View SolutionIn the arrangement shown in the following figure, the wavelength of light used is lambda . The distance between slits S_(1) and S_(2) is d (« D). The distance between S_(3) and S_(4) is u=lambda D // 3d . If the ratio of maximum to minimum intensity observed on screen is k. Find k.
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance >. Each source emits light of wavelength λ where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Which of the following is correct ?
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance >. Each source emits light of wavelength λ where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Which of the following is correct ?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs ?
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View Solution
