Two monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
the interference fringe on the screen are straight lines shape
the interference fringes on the screen are strainght lines perpendicular to the line S1S2A
point A is an intensity maxima if L=nλ
point A is always an intensity maxima for any separation L
The correct Answer is:c
If the screen is prependicular to y-axis (line joinin the sources), i.e., xz plane, the fringes will be circular (i.e., concentric circles with their centers on the point of intersection of the screen with y-axis). In this situation, central fringe will be bright id S1,S2=nλ and dark if S1S2=(2n−1)λ/2. From all this, it is clear that shape of fringes depends on the nature of sources and direction of observation, i.e., position of screen
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Multiple Correct
Explore 8 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Assertion- Reasoning
Explore 13 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Subjective
Explore 11 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:QUESTION BANK
Explore 34 Videos
- WAVESBook:CENGAGE PHYSICSChapter:WAVESExercise:QUESTION BANK
Explore 38 Videos
Similar Questions
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O

View Solution
Knowledge Check
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpointsTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesChoose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
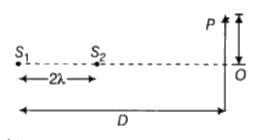 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5D
Two coherent point sources S1 and S2 are located at a distance 4l from each other. Perpendicular to the straight line joining S1 and S2 there is a large screen at a distance of 1000 λ from S1 as shown in Figure. Find the radius of the third maxima starting from the point 0.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionConsider two coherent monochromatic (wavelength λ) sources S1andS2 separated by a distance d. The ratio of intensity of S1 and that of S2 at point P is 4. The distance of P from S1 if the resultant intensity at point P is equal to 94, times the intensity due to S1 is : (n is a positive integer )
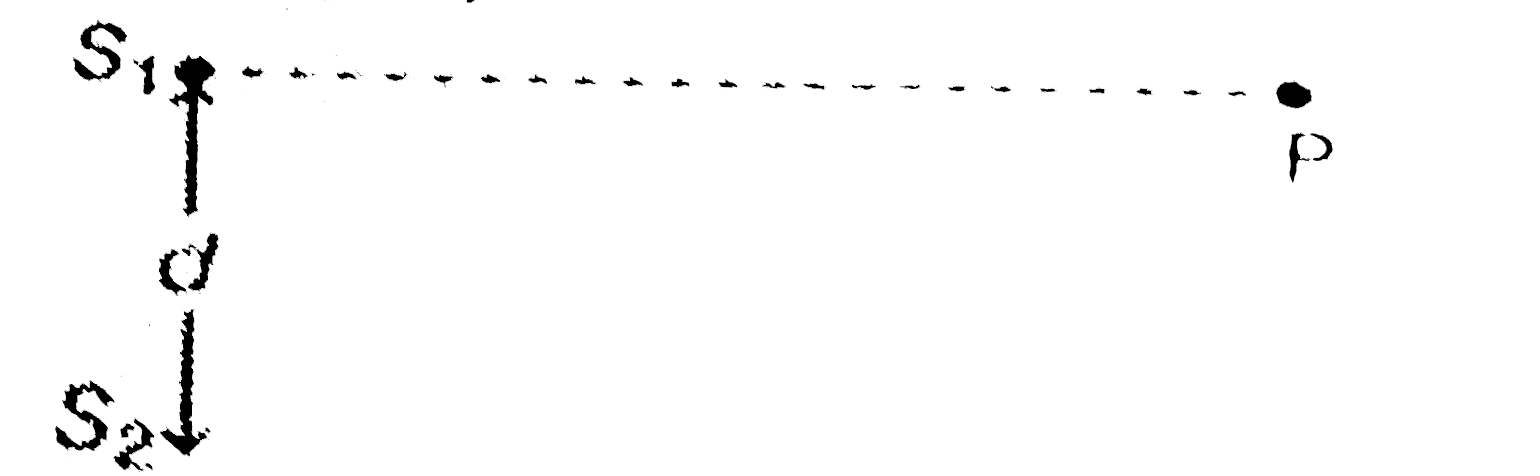
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View Solution

