A light wave of wavelength λ0 propagates from point A to point B. We introduce in its path a glass plate of refractive index n and thickness l. Then introduction of the plate alters the phase of the plate at B by an angle ϕ. If λ is the wavelength of light on emeriging from the plate, then
Δϕ=0
Δϕ=2πlλ0
Δϕ=2πl(1λ−1λ0)
Δϕ=2πlλ0(n−1)
The correct Answer is:c.,d
ϕf=2πλ0l
ϕf=2πλl
Δϕ=2πl(1λ−1λ0)
Further, by Snell's law,
nλ=(1)λ0⇒λl0n
⇒Δϕ=2πlλ0(n−1)
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionLight of wavelength 6000Å is incident on a thin glass plate of refractive index 1.5 such that angle of refraction into the plate is 60∘. Calculate the smallest thickness of plate which will make it appear dark by reflection.
View Solution
Knowledge Check
If d actual thickness of a plate of refractive index μ, then decrease in its thickness due to refraction of light will be
Ad(μ−1)BdμCd(1−1μ)Dd(μ−1)A ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
A33.7∘B23.7∘C43.7∘D53.7∘A ray of unpolarised light is incident on a glass plate of refractive index 1.54 at polarising angle, then angle of refraction is :
A33∘B44∘C57∘D90∘
Light reflected from the surface of glass plate of refractive index 1.57 is linearly polarised. Calculate the angle of refraction in glass.
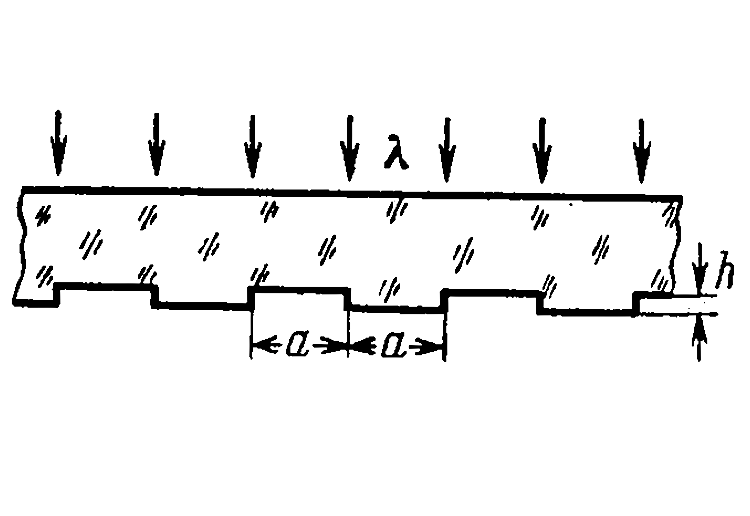
View SolutionA plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
View SolutionLight of wavelength λ0 in air enters a medium of refractive index n. If two points A and B in this medium lie along the path of this light at a distance x, then phase difference ϕ0 between these two point is
View SolutionWhen a mica plate of thickness 0.1 mm is introduced in one of the interfering beams, the central fringe is displaced by a distance equal to 10 fringes. If the wavelength of the light is 6000Å , the refractive index of the mica is
View SolutionA ray of light passes through a glass plate of thickness and refractive indexμ if the speed of light in vacuum is c,then the time taken by light in passing through the plate will be-
View Solution
