Consider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
d2−n2λ22nλ
d2+n2λ22nλ
nλd√d2−n2λ2
2nλd√d2−n2λ2
The correct Answer is:A
To solve the problem, we need to find the distance of point P from source S1 given the conditions of interference from two coherent sources S1 and S2. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- We have two coherent sources, S1 and S2, separated by a distance d.
- The ratio of their intensities is given as I1I2=4.
- The resultant intensity at point P is 94I1.
- The angle ∠S2S1P=90∘.
Step 2: Express Intensities
Let the intensity of source S1 be I1 and the intensity of source S2 be I2. From the given ratio:
I2=I14
Step 3: Write the Expression for Resultant Intensity
The resultant intensity I at point P due to two coherent sources is given by:
I=I1+I2+2√I1I2cosϕ
Where ϕ is the phase difference between the two waves at point P.
Step 4: Substitute Known Values
Substituting I2 into the intensity equation:
I=I1+I14+2√I1⋅I14cosϕ
This simplifies to:
I=I1+I14+2⋅I12cosϕ
I=I1+I14+I1cosϕ
I=54I1+I1cosϕ
Step 5: Set the Resultant Intensity Equal to Given Value
We know I=94I1:
54I1+I1cosϕ=94I1
Subtracting 54I1 from both sides:
I1cosϕ=94I1−54I1
I1cosϕ=44I1
cosϕ=1
Step 6: Determine the Phase Difference
Since cosϕ=1, the phase difference ϕ is:
ϕ=2nπ(n is a positive integer)
Step 7: Relate Phase Difference to Path Difference
The phase difference is related to the path difference Δ by:
ϕ=2πλΔ
Thus,
2nπ=2πλΔ
Cancelling 2π gives:
Δ=nλ
Step 8: Calculate Path Difference
The path difference Δ can also be expressed in terms of the distances:
Δ=√x2+d2−x
Setting the two expressions for path difference equal:
√x2+d2−x=nλ
Rearranging gives:
√x2+d2=nλ+x
Step 9: Square Both Sides
Squaring both sides:
x2+d2=(nλ+x)2
Expanding the right side:
x2+d2=n2λ2+2nλx+x2
Cancelling x2 from both sides:
d2=n2λ2+2nλx
Step 10: Solve for x
Rearranging gives:
2nλx=d2−n2λ2
x=d2−n2λ22nλ
Final Result
Thus, the distance of point P from source S1 is:
x=d2−n2λ22nλ
- We have two coherent sources, S1 and S2, separated by a distance d.
- The ratio of their intensities is given as I1I2=4.
- The resultant intensity at point P is 94I1.
- The angle ∠S2S1P=90∘.
Let the intensity of source S1 be I1 and the intensity of source S2 be I2. From the given ratio:
I2=I14
The resultant intensity I at point P due to two coherent sources is given by:
I=I1+I2+2√I1I2cosϕ
Where ϕ is the phase difference between the two waves at point P.
Substituting I2 into the intensity equation:
I=I1+I14+2√I1⋅I14cosϕ
This simplifies to:
I=I1+I14+2⋅I12cosϕ
I=I1+I14+I1cosϕ
I=54I1+I1cosϕ
We know I=94I1:
54I1+I1cosϕ=94I1
Subtracting 54I1 from both sides:
I1cosϕ=94I1−54I1
I1cosϕ=44I1
cosϕ=1
Since cosϕ=1, the phase difference ϕ is:
ϕ=2nπ(n is a positive integer)
The phase difference is related to the path difference Δ by:
ϕ=2πλΔ
Thus,
2nπ=2πλΔ
Cancelling 2π gives:
Δ=nλ
The path difference Δ can also be expressed in terms of the distances:
Δ=√x2+d2−x
Setting the two expressions for path difference equal:
√x2+d2−x=nλ
Rearranging gives:
√x2+d2=nλ+x
Squaring both sides:
x2+d2=(nλ+x)2
Expanding the right side:
x2+d2=n2λ2+2nλx+x2
Cancelling x2 from both sides:
d2=n2λ2+2nλx
Rearranging gives:
2nλx=d2−n2λ2
x=d2−n2λ22nλ
Thus, the distance of point P from source S1 is:
x=d2−n2λ22nλ
Topper's Solved these Questions
Similar Questions
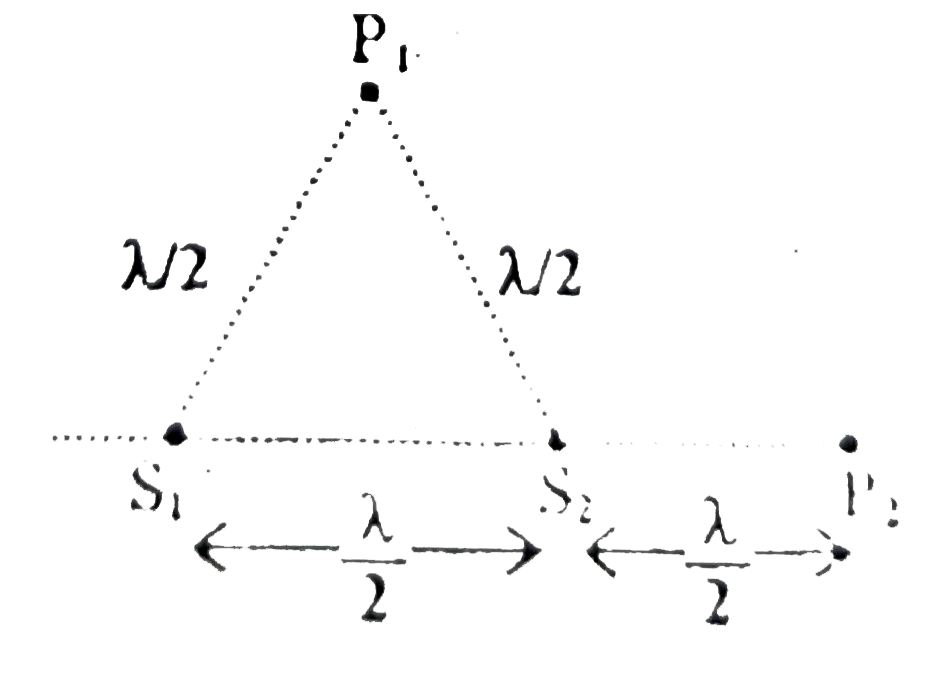
S1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
View SolutionTwo microwave sources S1 and S2 are located at a distance of 4λ from each other along Y-axis,with S1 at the origin as shown in the figure.A microwave detector D moves along the X-axis away from S1 .The first maximum is obtained for x equal to: (wavelength of the microwave is
View Solution
Knowledge Check
Consider two coherent monochromatic (wavelength λ) sources S1andS2 separated by a distance d. The ratio of intensity of S1 and that of S2 at point P is 4. The distance of P from S1 if the resultant intensity at point P is equal to 94, times the intensity due to S1 is : (n is a positive integer )
 Ad2−n2λ22nλBd2+n2λ22nλCnλd√d2−n2λ2D2nλd√d2−n2λ2
Ad2−n2λ22nλBd2+n2λ22nλCnλd√d2−n2λ2D2nλd√d2−n2λ2Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpointsTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circles
Two monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionWhen two waves of intensities l1andl2 coming from coherent sources interfere at a point P, where phase difference is ϕ, then resultant intensity (lres) at point P would be
View Solution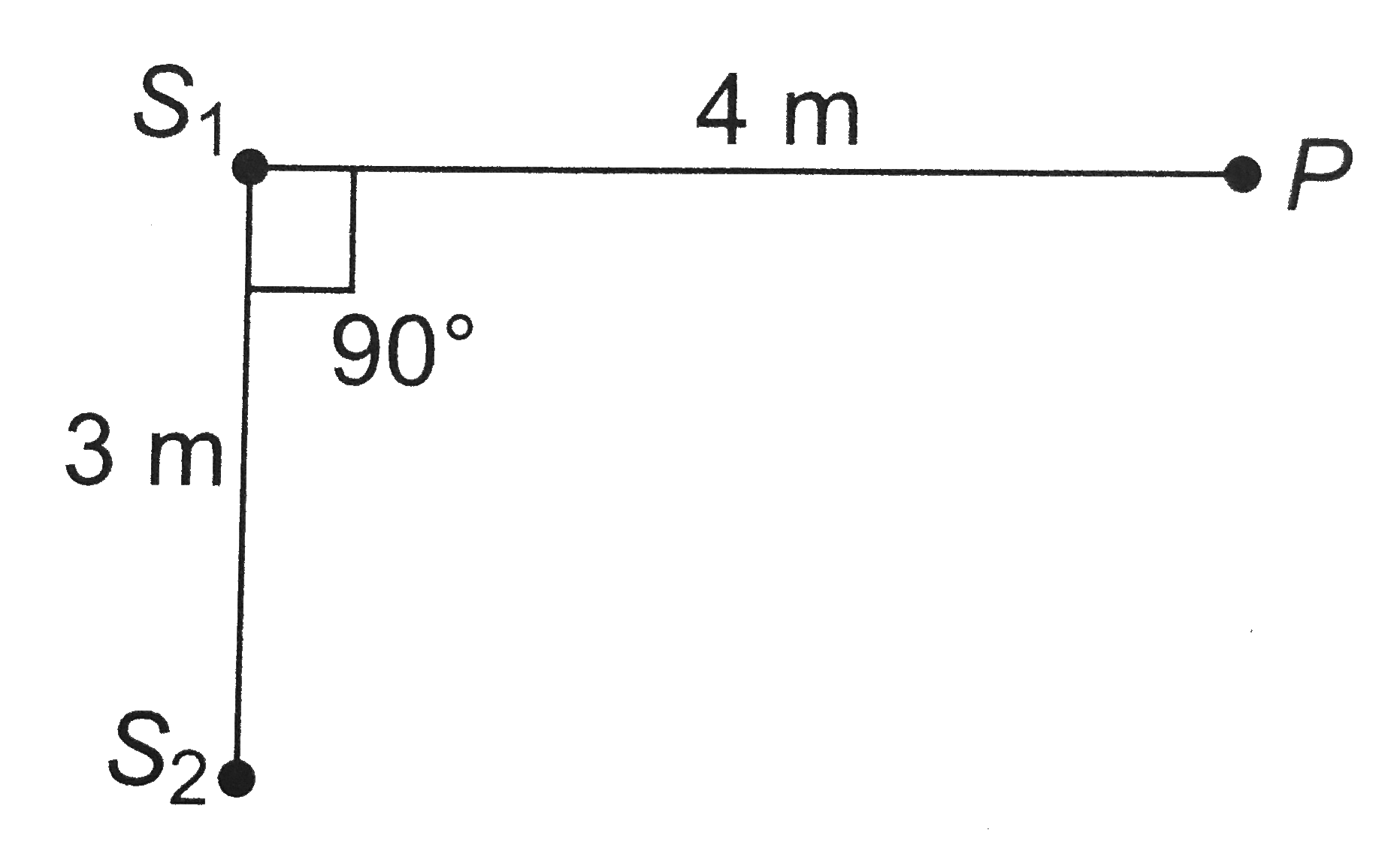
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View SolutionS1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
View SolutionRatio waves originating from sources S1 and S2 having zero phase difference and common wavelength λ will show completely destructive interference at a point P is S1P−S2P is
View Solution