A current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
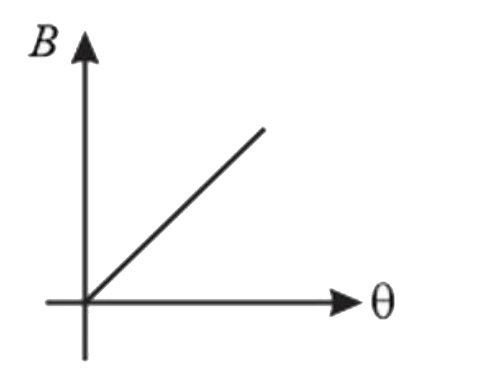
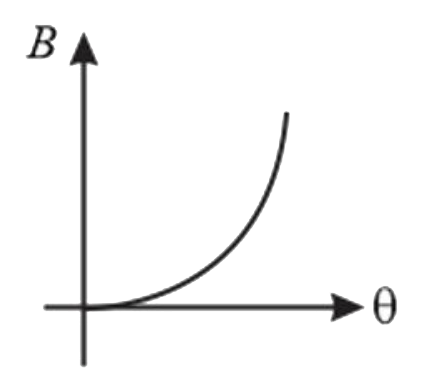
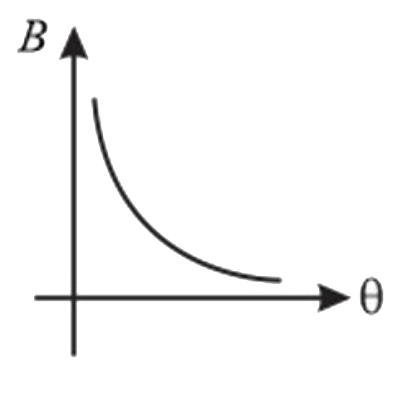
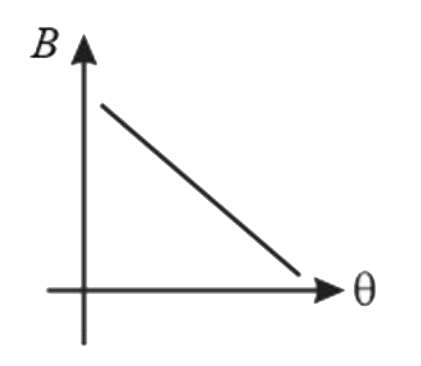
The correct Answer is:B
To solve the problem, we need to derive the relationship between the magnetic field B at the center of the arc and the angle θ subtended by the arc. Here are the steps to find the correct graph between B and θ:
Step 1: Understand the relationship between length of the wire and angle
The length of the arc L can be expressed in terms of the radius r and the angle θ (in radians) as:
L=rθ
Step 2: Express the radius in terms of length and angle
From the equation above, we can rearrange it to find the radius r:
r=Lθ
Step 3: Use the formula for magnetic field due to an arc
The magnetic field B at the center of an arc of radius r carrying a current I and subtending an angle θ is given by:
B=μ0Iθ4πr
where μ0 is the permeability of free space.
Step 4: Substitute the expression for r
Now, substituting the expression for r into the magnetic field equation:
B=μ0Iθ4π(Lθ)=μ0Iθ24πL
Step 5: Analyze the relationship between B and θ
From the equation B=μ0I4πLθ2, we can see that B is proportional to θ2. This indicates that as θ increases, B increases quadratically.
Step 6: Identify the graph type
The relationship B∝θ2 suggests that the graph of B versus θ will be a parabola opening upwards. Therefore, the correct graph will show B increasing as θ increases.
Conclusion
The correct graph between B and θ is a parabolic curve, which corresponds to the option that represents a quadratic relationship.
---
The length of the arc L can be expressed in terms of the radius r and the angle θ (in radians) as:
L=rθ
From the equation above, we can rearrange it to find the radius r:
r=Lθ
The magnetic field B at the center of an arc of radius r carrying a current I and subtending an angle θ is given by:
B=μ0Iθ4πr
where μ0 is the permeability of free space.
Now, substituting the expression for r into the magnetic field equation:
B=μ0Iθ4π(Lθ)=μ0Iθ24πL
From the equation B=μ0I4πLθ2, we can see that B is proportional to θ2. This indicates that as θ increases, B increases quadratically.
The relationship B∝θ2 suggests that the graph of B versus θ will be a parabola opening upwards. Therefore, the correct graph will show B increasing as θ increases.
The correct graph between B and θ is a parabolic curve, which corresponds to the option that represents a quadratic relationship.
Topper's Solved these Questions
Similar Questions
A piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA current carrying wire is bent into the shape of a square coil. The magnetic field produced at the entre of coil by one arm BC is B. Then the resultant magnetic field at the centre due to all the arms will be-
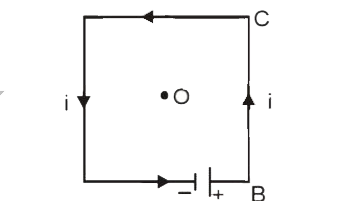
View Solution
Knowledge Check
A magnetised wire of moment M is bent into an arc of a circle subtending an angle of 60^(@) at the centre. The new magnetic moment is
 A(2M/π)B(M/π)C(3√3M/π)D(3M/π)
A(2M/π)B(M/π)C(3√3M/π)D(3M/π)A current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.
 Aμ0πiL(2π−θ3π)Bμ0πiL(2π−θ2π)Cμ0πiL(2π−θ)Dμ0πiL(2π+θ)2
Aμ0πiL(2π−θ3π)Bμ0πiL(2π−θ2π)Cμ0πiL(2π−θ)Dμ0πiL(2π+θ)2A current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
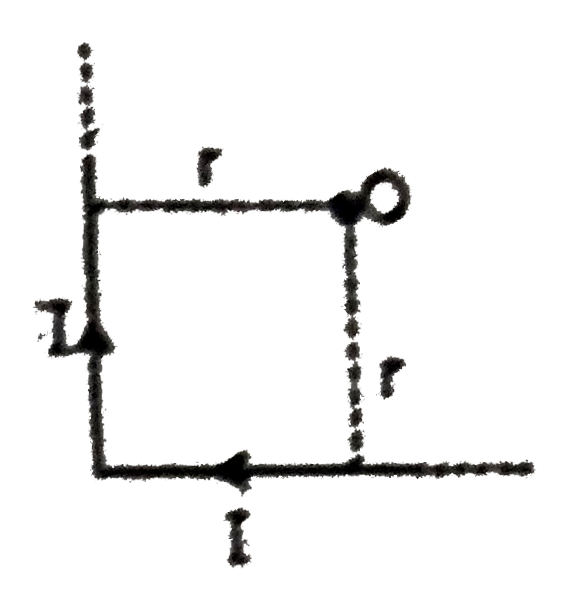 AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)
AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)
A wire of length 10cm is bent into an arc of a circle such that it subtends an angle of 1 radian at the centre. If a current of 1A is passed through the wire, the magnetic induction at the centre of the circle will be
View SolutionA wire of length 2 m carrying a current of 1 A is bent to form a circle, the magnetic moment of the coil is
View SolutionA wire of length 2 m carrying a current of 1 A is bent to form a circle, the magnetic moment of the coil is
View SolutionA wire of length 'L' is bent in to an arc of a circle and found to subtentd and angle of 'θ' radians at the centre.If a current of 'I' is passed through it, the magnetic induction at the center of the circle is
View SolutionA long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
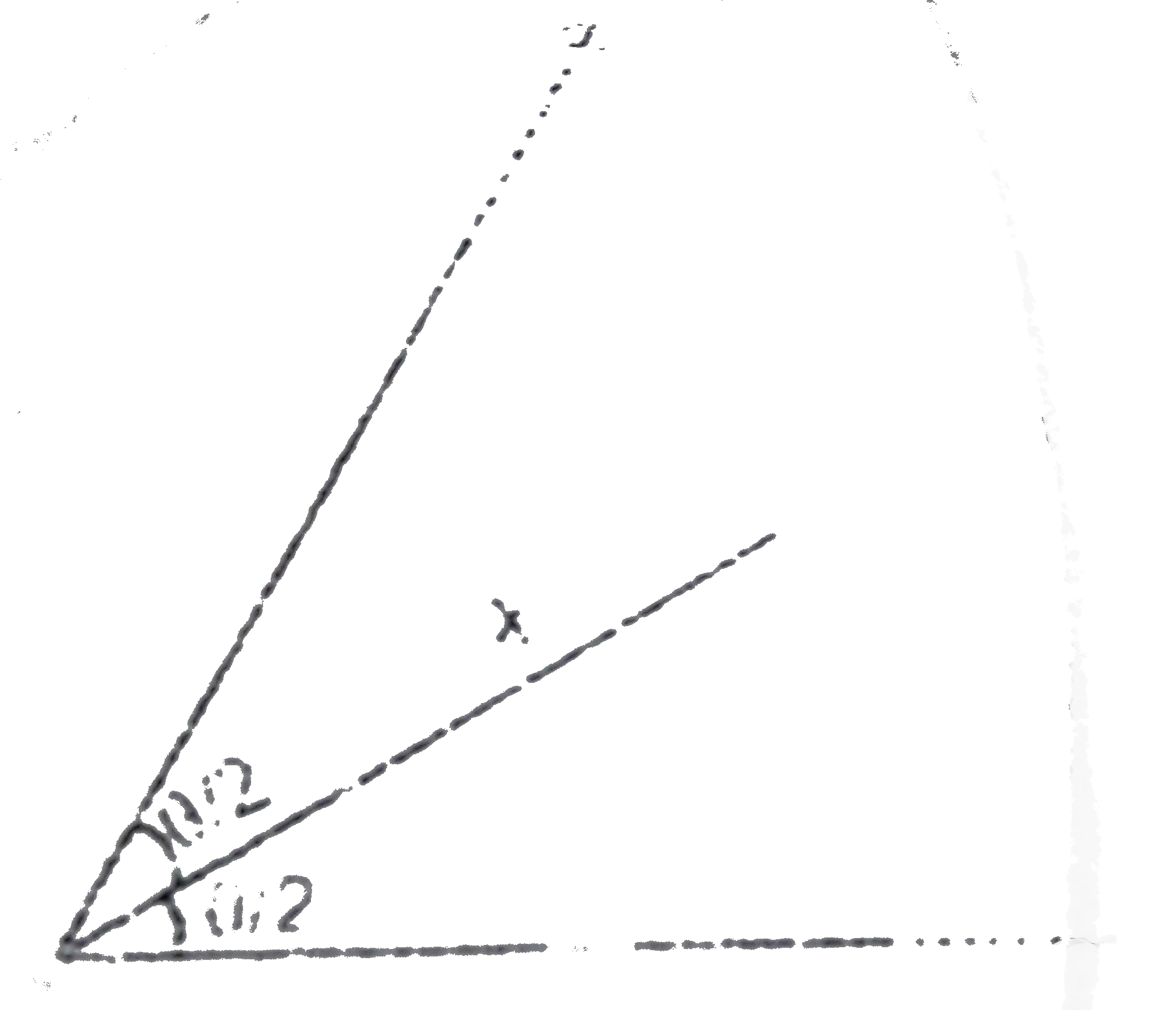
View Solution
