Two coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
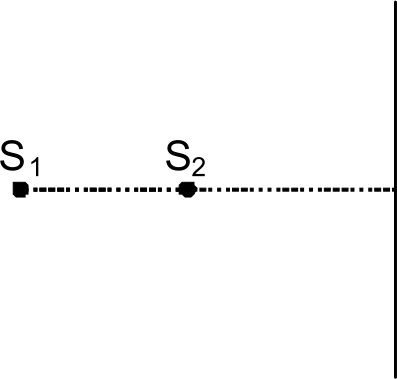
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
For S1S2=2.5λ, max path difference =2.5λ
min path difference =0
Between 2.5λ and 0 lie 2λ and λ⇒ two circular bright fringes
n1=2
For S1S2=5.7λ, max path difference =5.7λ
min path difference =0
Between 5.7λ and 0 lie 5λ,4λ,2λ,λ⇒ five circular bright fringes.
⇒n2=5
∴n2−n1=5−2=3
Topper's Solved these Questions
Similar Questions
Two point monochromatic and coherent sources of light of wavelength λ are each placed as shown in the figure below. The initial phase difference between the sources is zero. Select the incorrect statement.
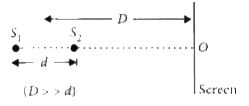
View SolutionTwo points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
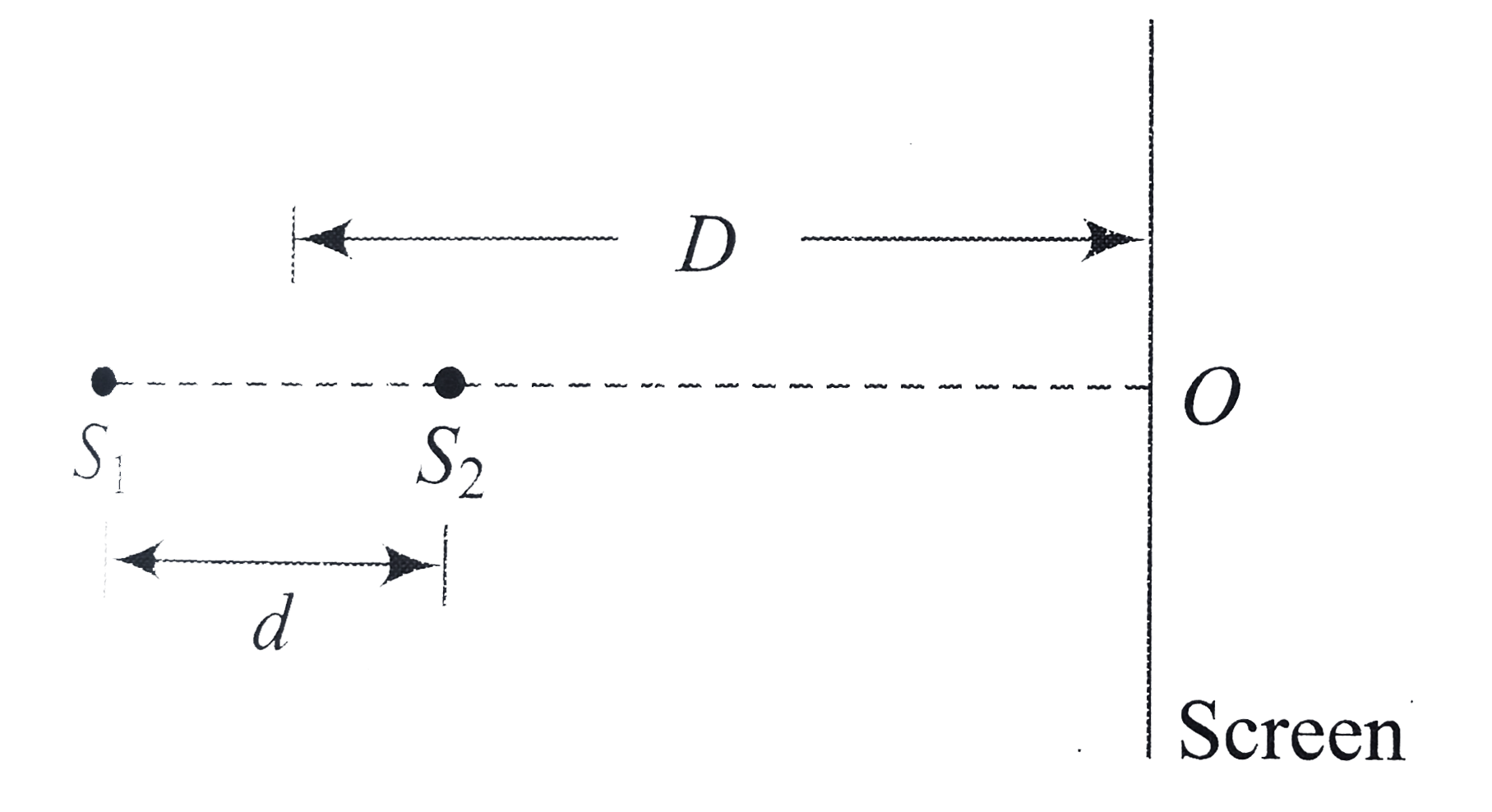
View Solution
Knowledge Check
Three coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.
 A2√2D7B√(17)D8C4√5DD4√2D7
A2√2D7B√(17)D8C4√5DD4√2D7Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpointsTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circles
Assertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.

Reason: For 11th order maxima path difference should be more.
View SolutionPath difference between two wavefronts emitted from coherent sources is 2.1μm. Phase difference between the wavefronts at that point is 7.692 πthe wavelength of light emitted by source will be
View SolutionS1 and S2 are two sources of sound emitting sine waves. The two sources are in phase. The sound emitted by the two sources interfers at point F. The waves of wavelength :

View SolutionTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
View SolutionTwo coherent sources S1 and S2 are kept on the edges of a step as shown in the figure. An infinitely long screen is placed on the right side of sources and lies at along y−z plane. Calculate total no. of maximas observed on the screen. PS1=8λ and PS2=6λ. Where λ is wavelength of light used. (There is no reflection from steps)
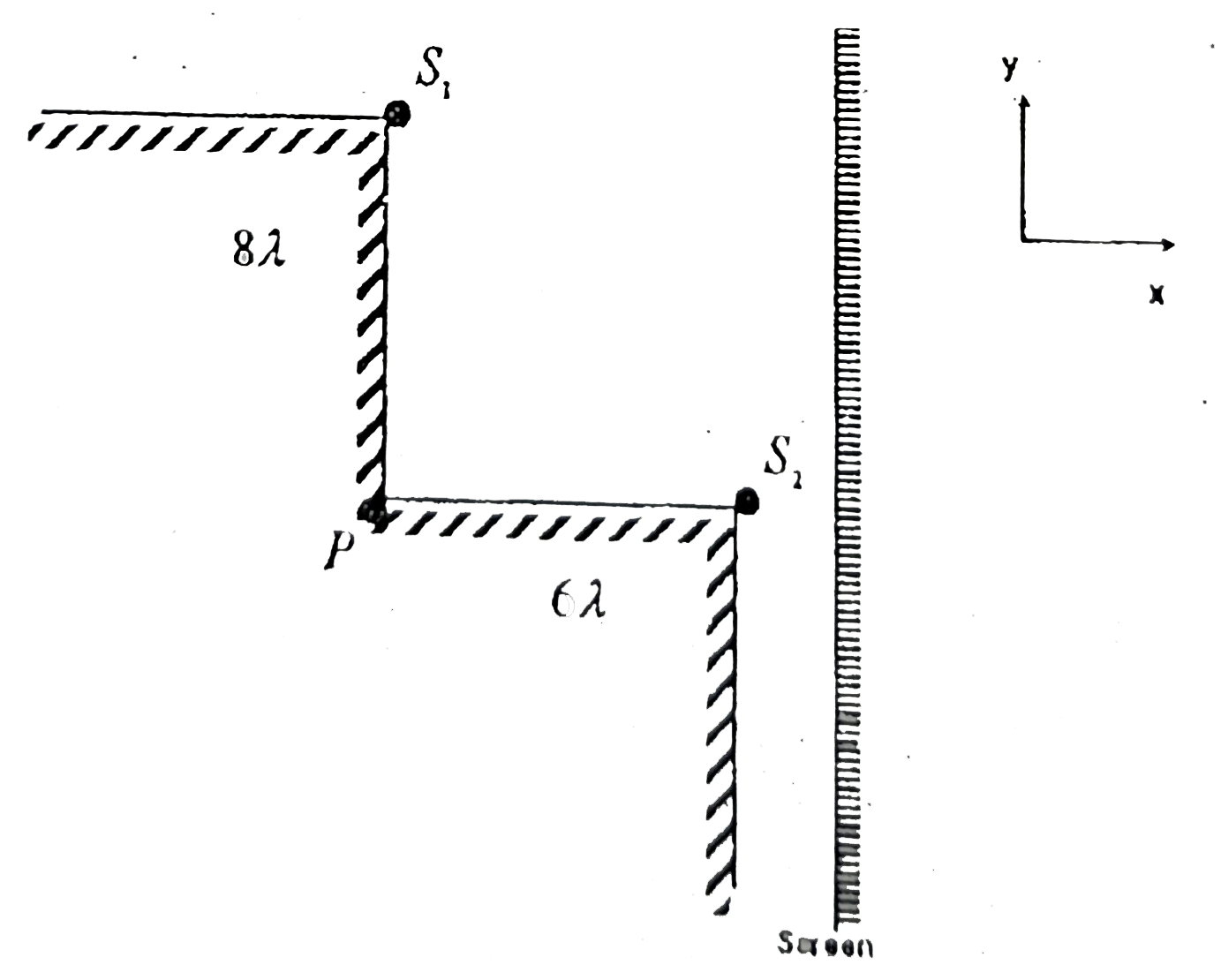
View Solution

