Consider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

The magnetic field within cylindrical region whose cross - section is indicated starts increasing at a constant rate α tesla/sec The graph showing the variation.of induced electric field with distance r from the axis of cylinder is :

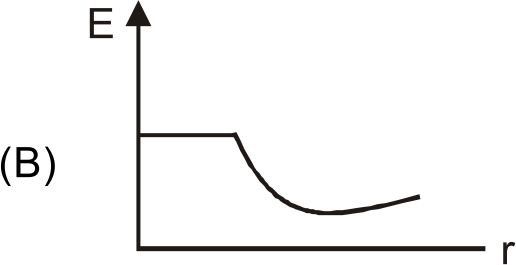

Explanation:
For rlt R ∮Edl=AdBdt
E2πr=(πr2)α
E=rα2 or E∝r
So, E-r graph is a straight line passing through origin.
At r=R, E=Rlapha2
for rgtR E2πr=(πR2)α
Hence , choice (a) is correct and choices (b),(c) and (d) are wrong.
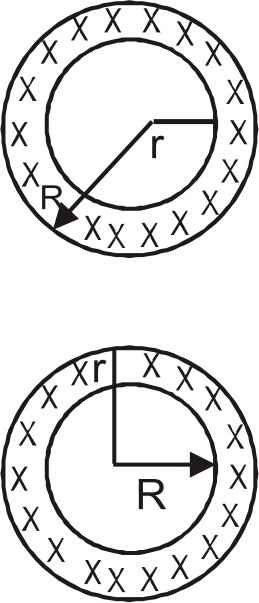
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionCurrent in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find
a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
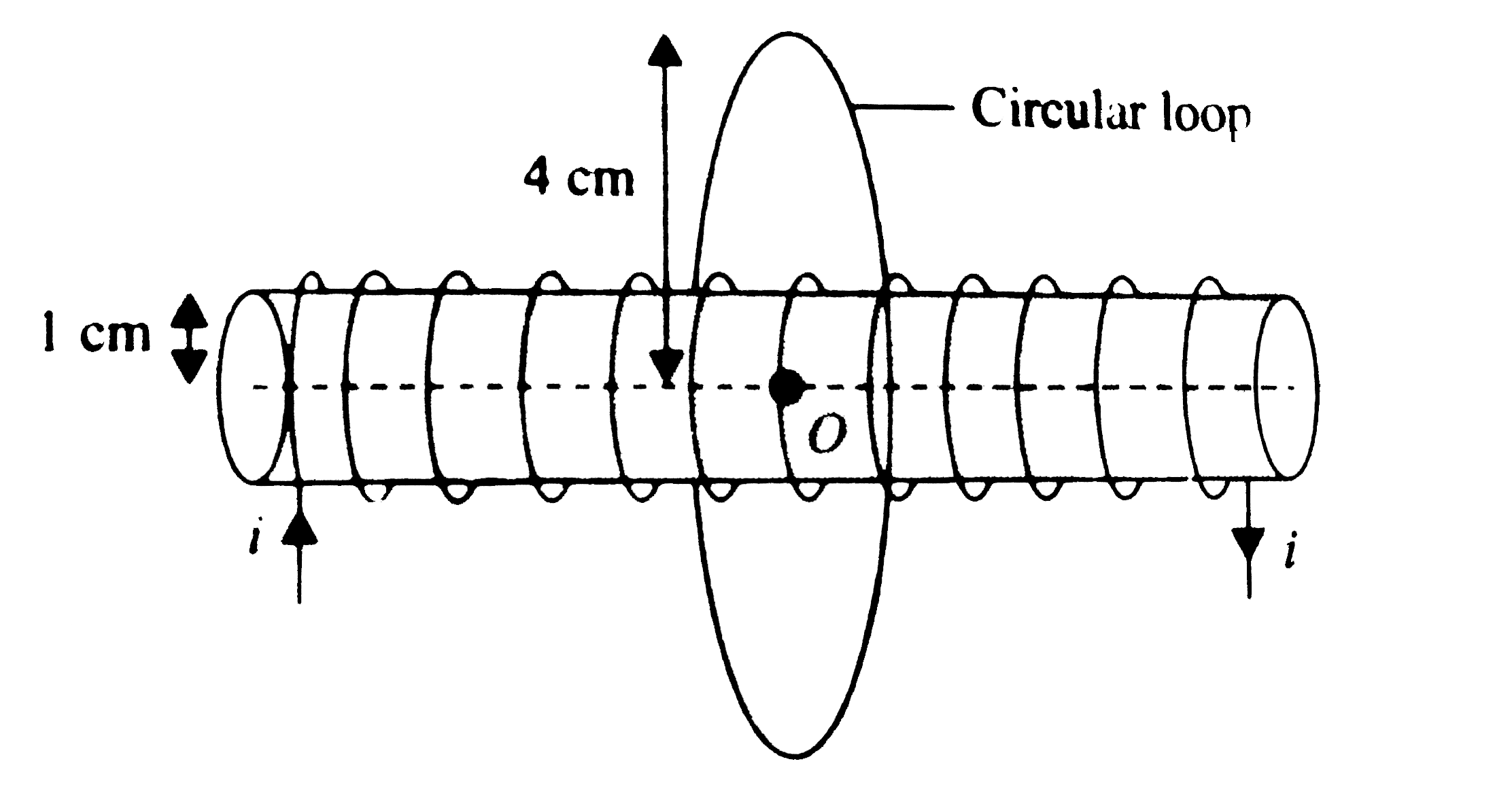
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.
View SolutionConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

A square non- conducting loop 20 cm on a side is placed in a magnetic field The centre of side AB coincides with the centre of magnetic field The magnetic field is increasing at the rate of 2T/s. Find the magnitude of line integral of induced electric field along path BC.
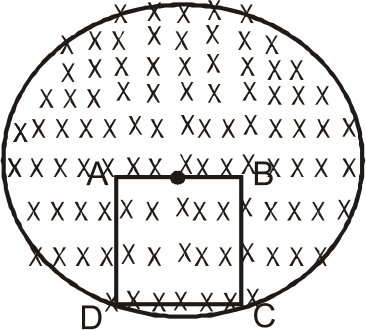
View SolutionConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced. e=-(dphi)/(dt) If resistance of loop is R then induced current. i=e/R For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move intvec(E).dvec(l)=e=-(dphi)/(dt) This induced electric field is non-electrostatic by nature. line integral of vec(E) around a closed path is non-zero Refer to above questions, Find the magnitude of line integral of induced electric field along path CD.
View SolutionThe total charge induced in a conducting loop when it is moved in magnetic field depends on
View SolutionAsseration: The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field. Reason: The emf is induced due to change in magnetic flux.
View SolutionThe magnetic field through a circular loop of wire 12 cm in radius and 8.5 ohm resistance, changes with time as shown in Fig. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot is as a function of time.
View SolutionAssertion If a loop is placed in a non-uniform (with respect to position) magnetic field, then induced emf is produced in the loop. Reason In a non-uniform magnetic field, magnetic flux passing through the loop will change. Therefore, induced emf is produced.
View SolutionA: When a conducting loop is kept stationary in a non-uniform magnetic field an emf is induced.
R: As per Faraday's law, whenever flux changes, an emf is induced.
View SolutionRead the following two statements.
(A) Emf can be induced by changing magnetic field.
(B) Emf must be induced when a conductor is moved inside magnetic field.
View SolutionA rectangular closed loop moves horizontally in a uniform magnetic field. i. Will there be any induced current in the loop if the loop is completely in the magnetic field? ii. Will there be any induced current in the loop if the loop is partially out of the magnetic field? iii. Will the induced current in the loop remain if the loop is stationary and the magnetic field changes with time?
View Solution(A): Total induced emf in a loop is not confined to any particular point but it is distributed around the loop.
(R): In general when there is no change in magnetic flux, no induced emf is produced
View Solution(A): When conducting loop is kept stationary in a non-uniform magnetic field an emf is induced. (R): As per Faraday's law, whenever flux changes, an emf is induced.
View Solution

