All sides of an equilateral triangle are diameter of three identical uniform semi- circular rings each of mass m. Plane of each ring is perpendicular to the plane of paper. Then moment of inertia of this system of three semicircular rings about an axis through centroid of triangle and perpendicular to plane of paper is :
5ma224
5ma216
5ma28
5ma26
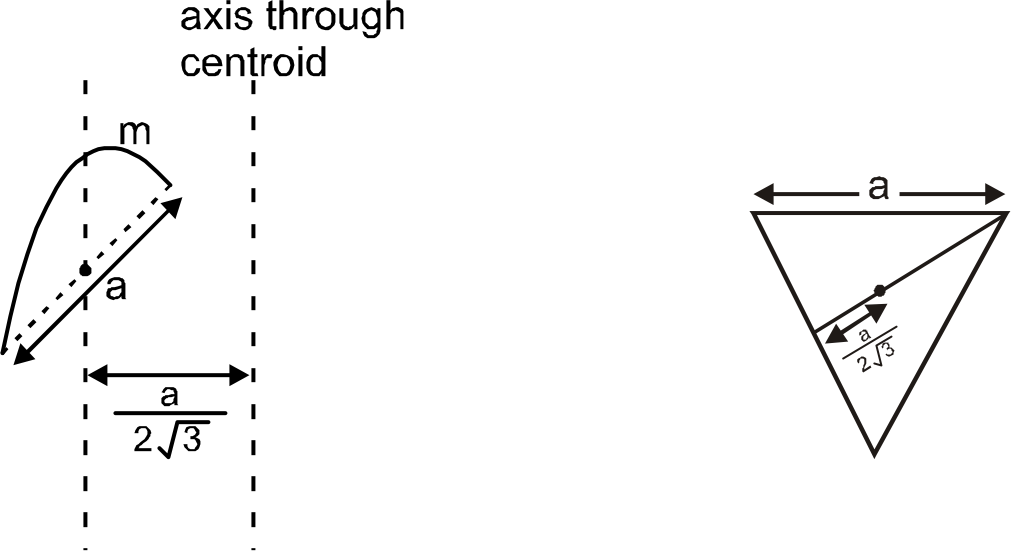
I'=Icm+m(a2√3)2=5ma224=Icm=m(a2)22=ma28
I=3I'=5ma28
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is I_(A) . If I_(C ) is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C , then
View SolutionThree particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
View SolutionTwo rings of the same mass and radius are placed such that their centers are at a common point and their planes are perpendicular to each other . The moment of inertia of the system about an axis passing through the diameter of one of the rings is I . Then moment of inertia of one of the ring of the system about the central axis and perpendicular to its plane would be
View SolutionThree particles each of mass 100 g are placed at the vertices of an equilateral triangle of side length 10 cm. Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
View SolutionThree particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View SolutionThree identical rings, each of mass M and radius R are placed in the same plane touching each other such that their centers from the vertices of an equilateral triangle. The M.I of the system about an axis passing through center of one of the rings and perpendicular to its plane is
View SolutionThree particles each of mass 100 g are placed at the vertices of an equilateral triangle of side length 10 cm. Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
View SolutionThree particles each of mass 100g are placed at the vertices of an equilateral triangle of side length 10cm . Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
View SolutionTwo identical concentric rings each of massMand radius R are placed perpendicular to each other. What is the moment of inertia about an axis passing through the center of this system and perpendicular to the plane of one of the rings?
View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is I_(A) . If I_(C ) is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C , then
View SolutionAll sides of an equilateral triangle are diameter of three identical uniform semi- circular rings each of mass m. Plane of each ring is perpendicular to the plane of paper. Then moment of inertia of this system of three semicircular rings about an axis through centroid of triangle and perpendicular to plane of paper is :

View SolutionThree particles each of mass 'm' are kept at the three vertices of an equilateral triangle of side 'a'. Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
View Solution

