In a regular YDSE, when thin film of refractive index mu is placed in front of the upper slit then it is observed that the intensity at the central point becomes half of the original intensity. It is also observed that the initial 3^(rd) maxima is now below the central point and the initial 4th minima is above the central point. Now, a film of refractive index μ1 and thickness same as the above film. is put in the front of the lower slit also. It is observed that whole fringe pattern shifts by one fringe width. What is the value of μ1 ?
(4μ+9)/12
(4μ+9)/13
(4μ+9)/11
None
The correct Answer is:B
Δϕ=2πλt(μ−1)....(1)
6π<Δϕ<7π.......(2)
I=I0cos2(Δϕ2)
I=I0/2
⇒cos(Δϕ2)
I=I0/2
⇒cos(Δϕ2)=±1√2⇒Δϕ2=2nπ±π4
Δϕ=4nπ±π/2.....(3)
Solving equation (2)&(3)we get
Δϕ=6.5π
om(1)6.5π−2πλt(μ−1)....(4)
Introducing record film shifted the fringed pattern by one fringe with means.
t(μ−1)=λ....(5)
Solving 4 & 5
⇒μ1=4μ+913

Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Comphrehension
Explore 134 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Reasoning
Explore 75 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
The velocity- time graph of car moving on a straight track is given below. The car weight 1000kg.
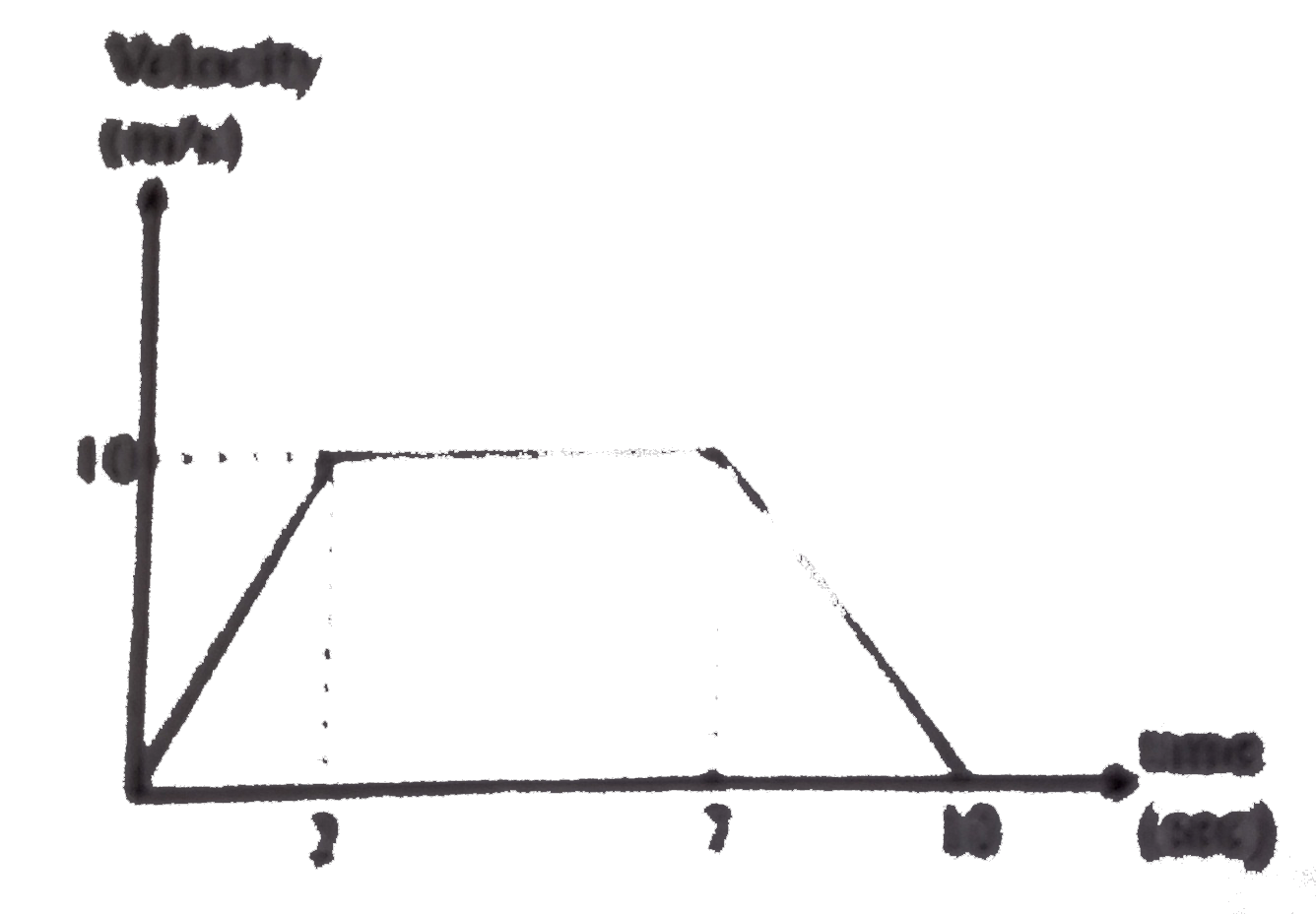 The distance travelled by the car during the whole motion is:
The distance travelled by the car during the whole motion is:
View SolutionStatement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
View SolutionIn YDSE when slab of thickness t and refractive index mu is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of lambda and mu .
View SolutionIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
View SolutionIn YDSE, let A and B be two slits. Films of thickness t_(A) and t_(B) and refractive mu_(A) and mu_(B) are placed in front of A and B, respectively. If mu_(A) t_(A) = mu_(A) t_(B) , then the central maxima will
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index mu is placed in front of A. Let beta = fringe width. Then the central maxima will shift
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2mu and mu .Find the position (y) of central maxima.
View SolutionIn a young's double slit experiment ,let A and B be the two slits.A thin film film of thickness t and refractive index mu is pklaced in front of A .Let beta =fringe width.The central maximum will shift:
View SolutionIn the Young's double slit experiment the central maxima is observed to be I_(0) . If one of the slits is covered, then intensity at the central maxima will become-
View SolutionIn a Young's double slit experiment. Let A and B be the two slits. A thin film of thickness t and refractive index mu is placed in front of A. Let beta = frine width. The central maximum will shift :
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionIn A young.s double - slit experiment ,let A and B be two slits , A thin film of thickness t and refractive index mu is placed in front of A .Let beta = fringe width .The central maximum will shift .
View Solutionयदि द्वि-स्लिट प्रयोग में माना A तथा B दो स्लिट है। एक पतली फिल्म की मोटाई t व अपवर्तनांक μ है तथा जो A के सामने रखी है। माना β = फ्रिज चौडाई अतः केन्द्रिय उच्चिष्ठ स्थानान्तरित होगा
View Solution

