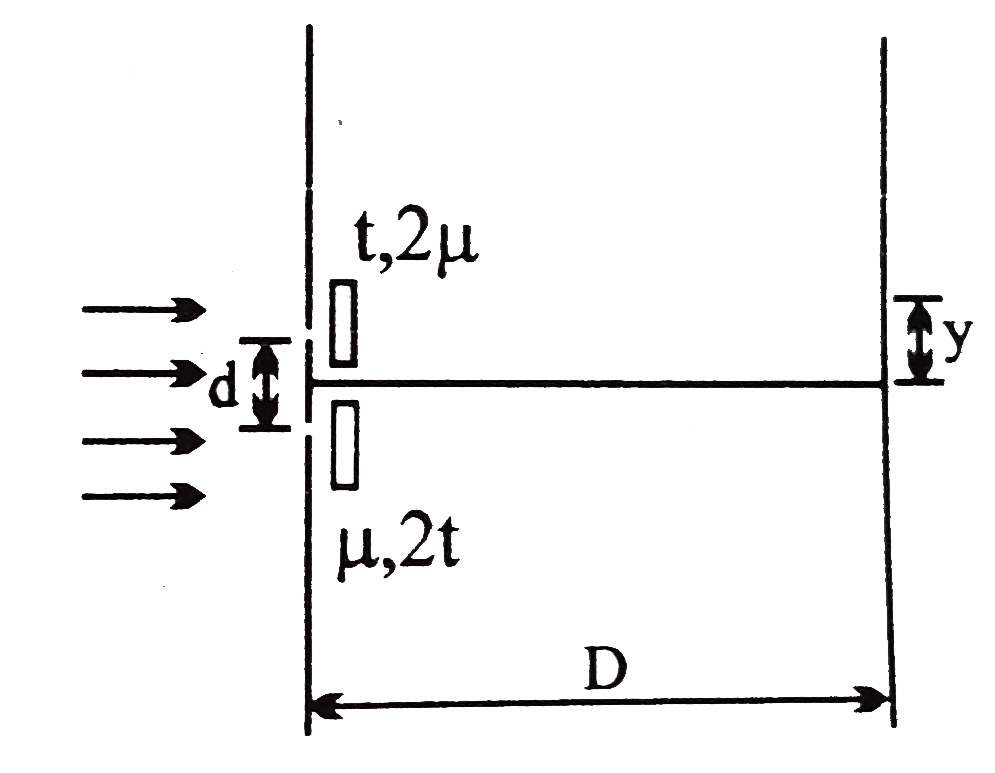
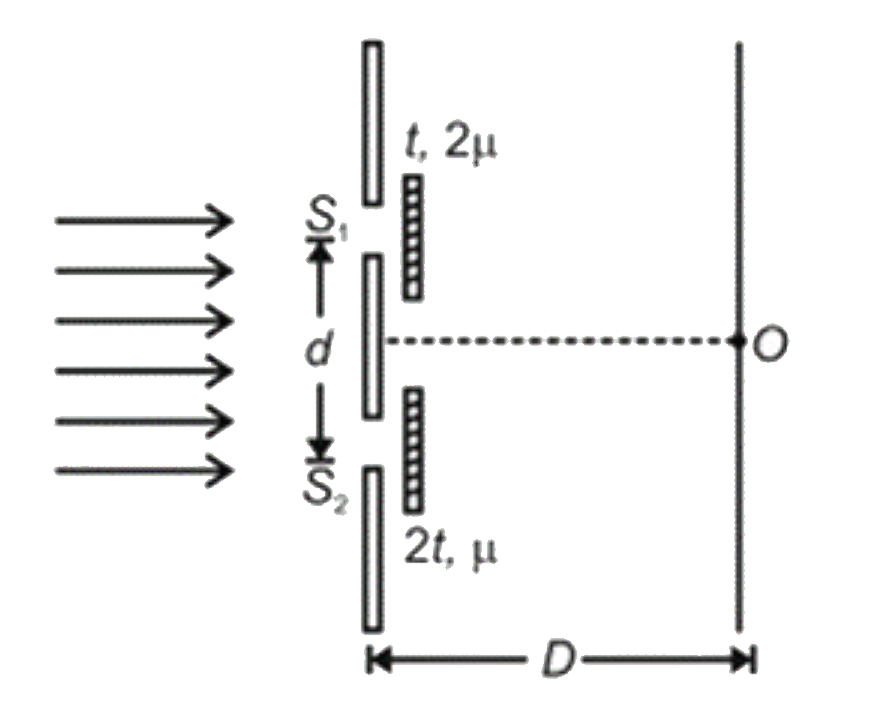
In the YDSE shown the two slits are covered with thin sheets having thickness t&2t and refractive index 2μand μ .Find the position (y) of central maxima.
zero
tDd
−tDd
none
The correct Answer is:B
Path.diff=(S2P−2t+μ.2t)−[(S1P−t)+2μt)]
Path diff.=(S2P−S1P)−t
Path diff.=yDD−t
since central maximum is at point P
ydD−t=0⇒y=tDd
Similar Questions
In the YDSE shown below, two slits are covered with thin sheets having a thickness t and 2t and refractive indices 2μ and μ respectively. The position of central maxima is shifted by a distance of N (in cm) from the central position of the screen. Find the value of N.
[d=1mm,D=1m,t=2×10−2mm,μ=32]
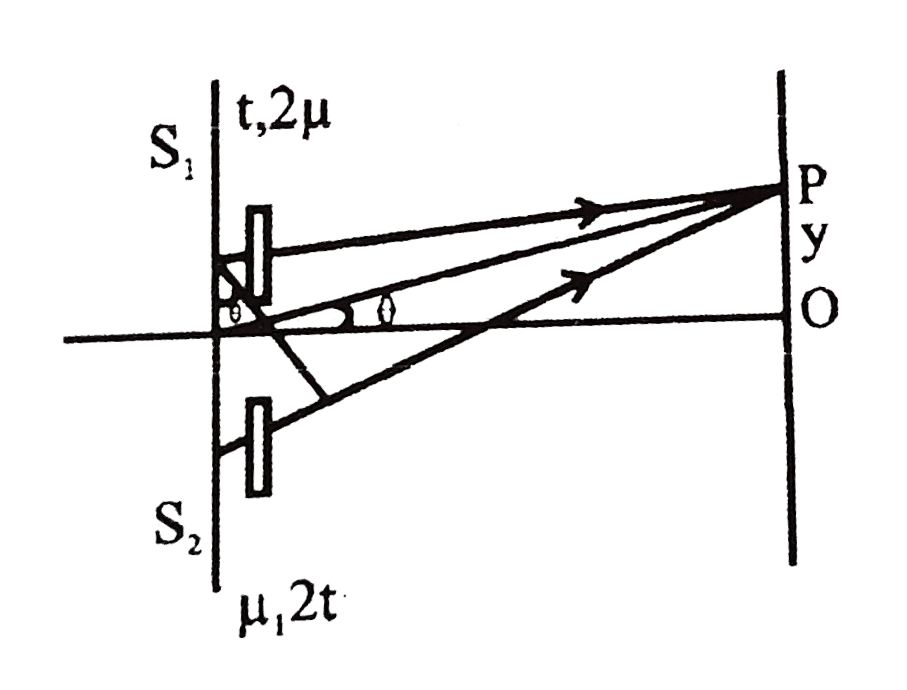
View SolutionIn a double slit experiment a parallel beam of light strikes the slit plane at an angleθ as shown in the figure. The two slits are covered with transparent plastic sheets of equal thickness t but of different refractive indices 1.2 and 1.5. The central maxima is formed at the centre of the screen at C.
(a) Which sheet was used to cover the slit S1?
(b) Findθ.
View Solution
Knowledge Check
There is a Young's double-slit experiment set-up completely dipped in water. Assume that the refractive index of water is μ1. One of the slits is covered with a thin film of thickness t and refractive index μ2. What will be the optical path difference at the centre of screen ?
A|(μ2−μ1)t|B|(μ2−1)t|C∣∣∣(μ2μ1−1)t∣∣∣D∣∣∣(μ1μ2−1)t∣∣∣In Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
Atoward ABtoward BCby t(μ−1)βλDby μtβλIn a young's double slit experiment ,let Aand B be the two slits.A thin film film of thickness t and refractive indexμ is pklaced in front of A.Let β =fringe width.The central maximum will shift:
Atowards ABtowards BCby t(μ−1)βλDby μtβλ
A monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
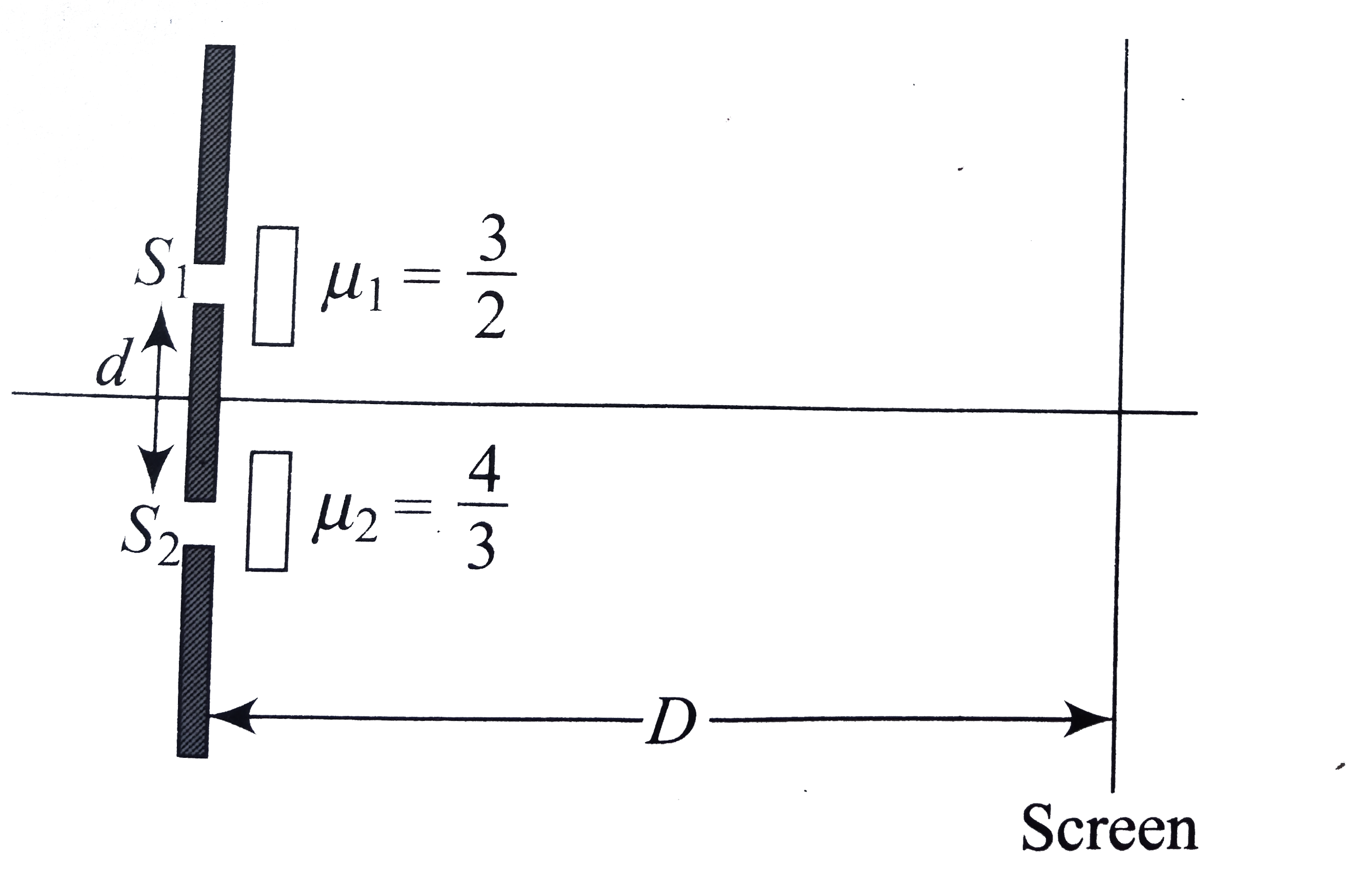
View SolutionA Young's double slit apparatus is immersed in a liquid of refractive index μ1. The slit plame touches the liquid surface. A parallel beam of monochromatic light of wavelength λ (in air) is incident normally on the slits.
a. Find the fringe width.
b. If one of the slits (say S2) is covered by a transparent slab of refrative index μ2 and thickless t as shown, find the new position of central maxima.
c. Now, the other slit, S1 is also covered by a slab of same thickness and refractive index μ3 as shown in Fig. 2.49 due to which the central maxima recovers it positon, find the value of μ3
Find the ratio of intensities at O in the three conditions (a), (b), and (c).
View SolutionIn Young’s double slit experiment a transparent sheet of thickness t and refractive index μ is placed in front of one of the slits and the central fringe moves away from the central line. It was found that when temperature was raised byΔθthe central fringe was back on the central line (at C). It is known that temperature coefficient of linear expan- sion of the material of the transparent sheet isα. A young scientist modeled that the refractive index of the material changes with temperature as Δμ=–gamaΔθ. Find Δθ in terms of other given quantities. D and d are given and have usual meaning.
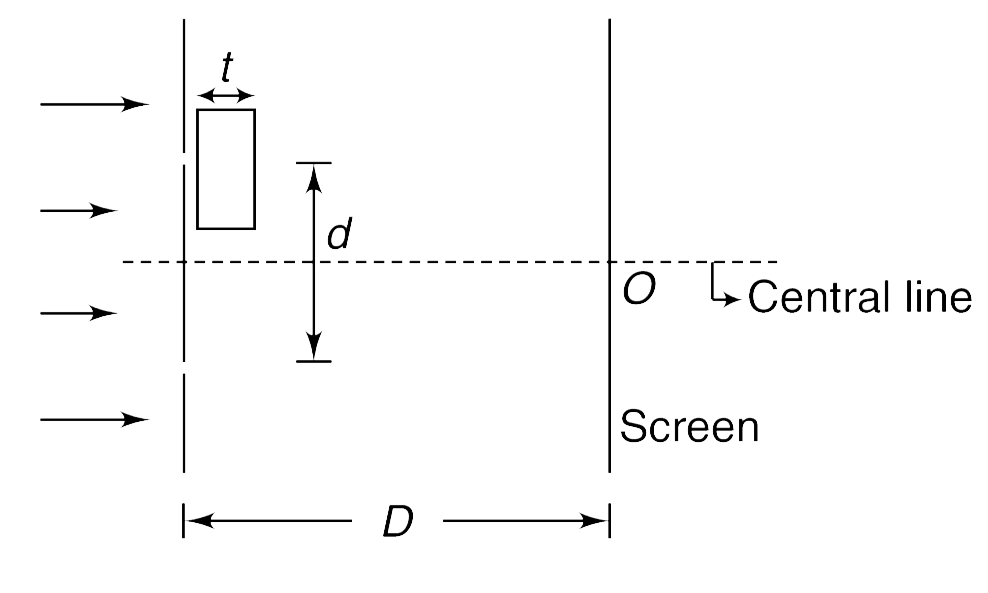
View SolutionIn Young's double-slit experiment, if both the slits are covered by a thin transparent sheet of thickness t and refractive index n, the optical path difference between the two interfering waves
View SolutionYDSE is carried with two thin sheets of thickness 10.4μ m each and refractive index μ1=1.52andμ2=1.40 covering the slits S1andS2 respectively. If white light of range 400nm to 780 nm is used, then which wavelength will form maxima exactly at point O, the centre of the screen

View Solution

