YDSE is carried with two thin sheets of thickness 10.4μ m each and refractive index μ1=1.52andμ2=1.40 covering the slits S1andS2 respectively. If white light of range 400nm to 780 nm is used, then which wavelength will form maxima exactly at point O, the centre of the screen

(a) 416 nm only
(b) 624 nm only
(c)416 nm and 624nm only
None of these
The correct Answer is:C
Δx1=(μ1−1),Δx2=(μ2−1)t
∴Δx=(μ1−μ2)t
=(1.52−1.40)(10400nm)
=1248 nm
For maximum intensity,
Δx=1248=nλ
∴λ=1248n
For n=2,λ=624nm
and for n=3,λ=416nm .
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Subjective Questions
5 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
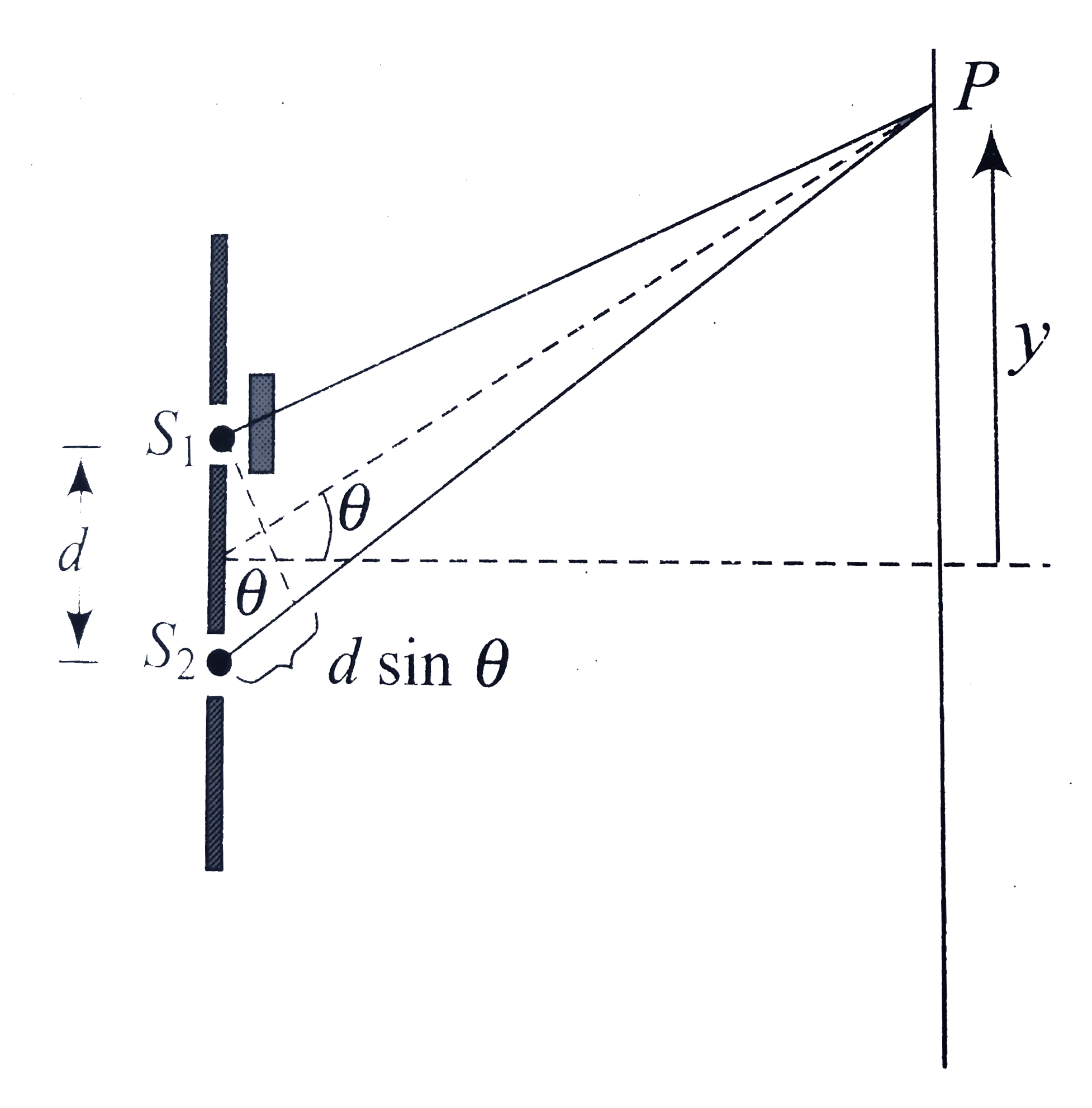
Two transparent sheets of thickness t1 and t2 and refractive indexes μ1 and μ2 are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

[D[(μ1−1)t1−(μ2−1)t2]d,(μ2−1)t2]
View SolutionYoung’s double slit experiment is done in a medium of refractive index 4/3. Light of 600 nm wavelength is falling on the slits having 0.45 pm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 pm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown.
(a) Find the location of central maxima (bright fringe with zero I t y path difference) on the y-axis.
(b) Find the light intensity at point O relative to the maximum fringe intensity.
(c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that from maxima exactly at point O[All wavelengths in this problem are for the given medium of refractive index 43. Ignore dispersions.]
View Solution
Knowledge Check
In YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:
 A650 nmB625 nmC550 nmD605 nm
A650 nmB625 nmC550 nmD605 nmIn the YDSE shown the two slits are covered with thin sheets having thickness t&2t and refractive index 2μand μ .Find the position (y) of central maxima.
 AzeroBtDdC−tDdDnone
AzeroBtDdC−tDdDnoneA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
A2 fringes upwardB2 fringes downwardC10 fringes upwardDNone of these
The young's double slit experiment is done in a medium of refractive index 4/3.A light of 600nmwavelength is falling on the slits having 0.45 mm separation .The lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index1.5.the intereference pattern is observed ona screen placed 1.5m from the slits are shown
(a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis.
(b) Find the light intensity at point Orelative to the maximum fringe intensity.
(c )Now,if 600nmlight is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O.[All wavelengths in this problem are for the given medium of refractive index 4/3 .Ignore dispersion]
View SolutionThe wavelength range of white light is 400 nm to 700 nm. What will be the wavelength range if light passes through water? Refractive index of water is 1.33.
View SolutionOil film of thickness 1μm is deposited on a glass plate. Refractive index of oil is 1.25 and that of the glass is 1.5. Which wavelength in the visible region (400 nm to 700 nm) will be strongly reflected by this film?
View SolutionIn YDSE, light of wavelength λ=5000Å is used, which emerges in phase from two slits distance d=3×10−7m apart. A transparent sheet of thickness t=1.5×10−7m, refractive index n=1.17, is placed over one of the slits. Where does the central maxima of the interference now appear from the center of the screen? (Find the value of y?)
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View Solution
