In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
λ(2μ−1)
2λ(2μ−1)
λ(μ−1)
2λ(2μ+1)
The correct Answer is:C
Step by step video, text & image solution for In YDSE when slab of thickness t and refractive index mu is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of lambda and mu. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a YDSE experiment, the distance between the slits & the screen is 100cm. For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width 0.25mm. When the distance between the slits is increased by Δd=1.2mm, the fringe width decreased to n=2/3 of the original value. In the final position, a thin glass plate of refractive index 1.5 is kept in front of one of the slits & the shift of central maximum is observed to be 20 fringe width. Find the thickness of the plate & wavelength of the incident light.
View SolutionIn Young’s double slit experiment a transparent sheet of thickness t and refractive index μ is placed in front of one of the slits and the central fringe moves away from the central line. It was found that when temperature was raised byΔθthe central fringe was back on the central line (at C). It is known that temperature coefficient of linear expan- sion of the material of the transparent sheet isα. A young scientist modeled that the refractive index of the material changes with temperature as Δμ=–gamaΔθ. Find Δθ in terms of other given quantities. D and d are given and have usual meaning.
View Solution
Knowledge Check
In YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
Aβ(μ−1)t2λBβ(μ−1)tλCβ(μ−1)t3λDβ(μ−1)t4λIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
Atoward ABtoward BCby t(μ−1)βλDby μtβλIn Young’s experiment, monochromatic light through a single slit S is used to illuminate the two slits S1and S2. Interference fringes are obtained on a screen. The fringe width is found to be w. Now a thin sheet of mica (thickness t and refractive index μ) is placed near and in front of one of the two slits. Now the fringe width is found to be w’, then :
Aw'=w/μBw'=wμCw'=(μ−1)twDw'=w
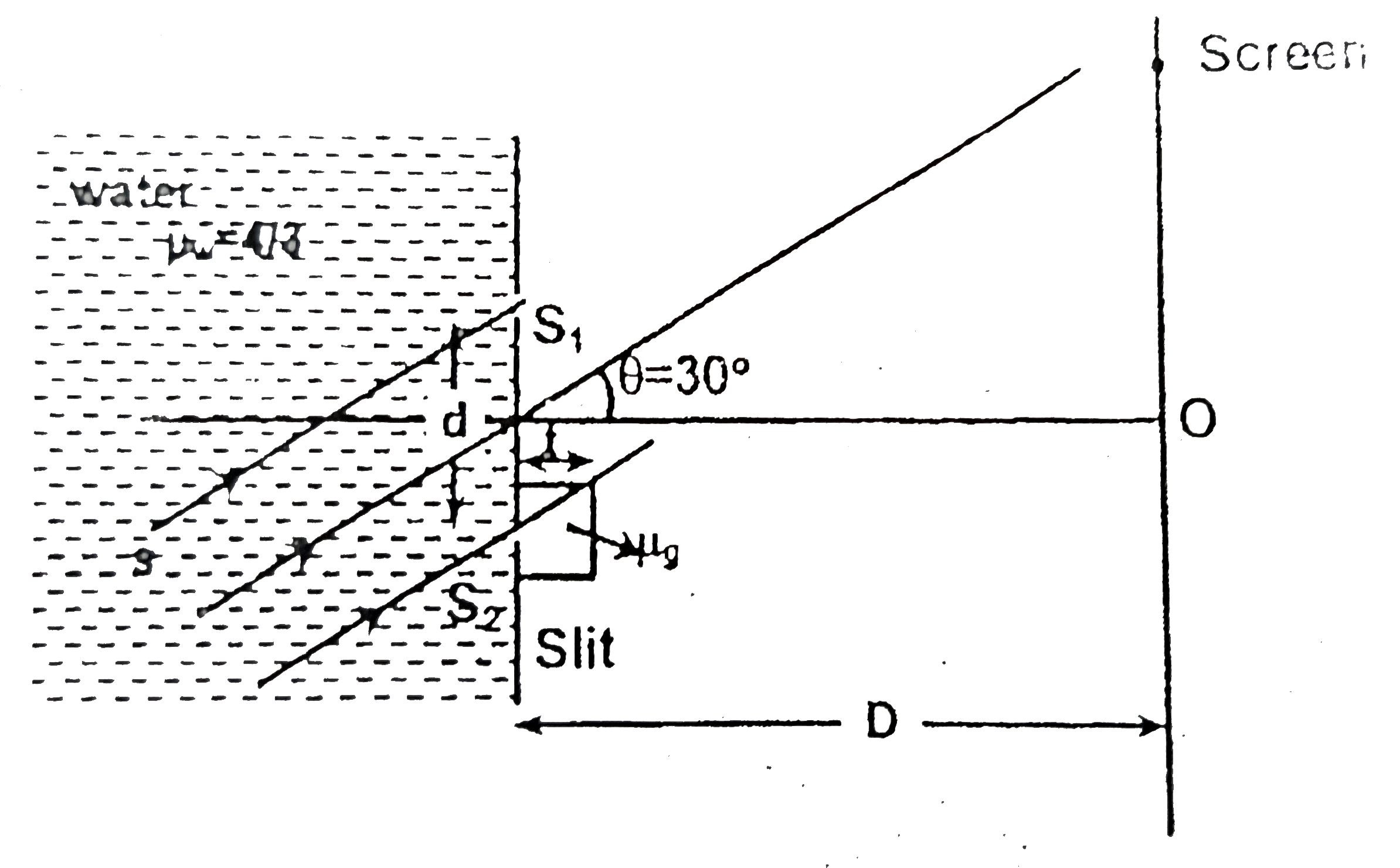
In a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
View SolutionA plate of thickness t made of a material of refractive index μ is placed in front of one of the slits in a double slit experiment. (a) Find the changes in he optical path due to introduction of the plate. (b) Wht should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ? Wavelength of the light used is λ. Neglect any absorption of light in the plate.
View SolutionIn a young's double slit experiment ,let Aand B be the two slits.A thin film film of thickness t and refractive indexμ is pklaced in front of A.Let β =fringe width.The central maximum will shift:
View SolutionWhen a thin transparent plate of thickness t and refractive index μ is placed in the path of one the two interfering waves of light, then the path difference changes by
View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.
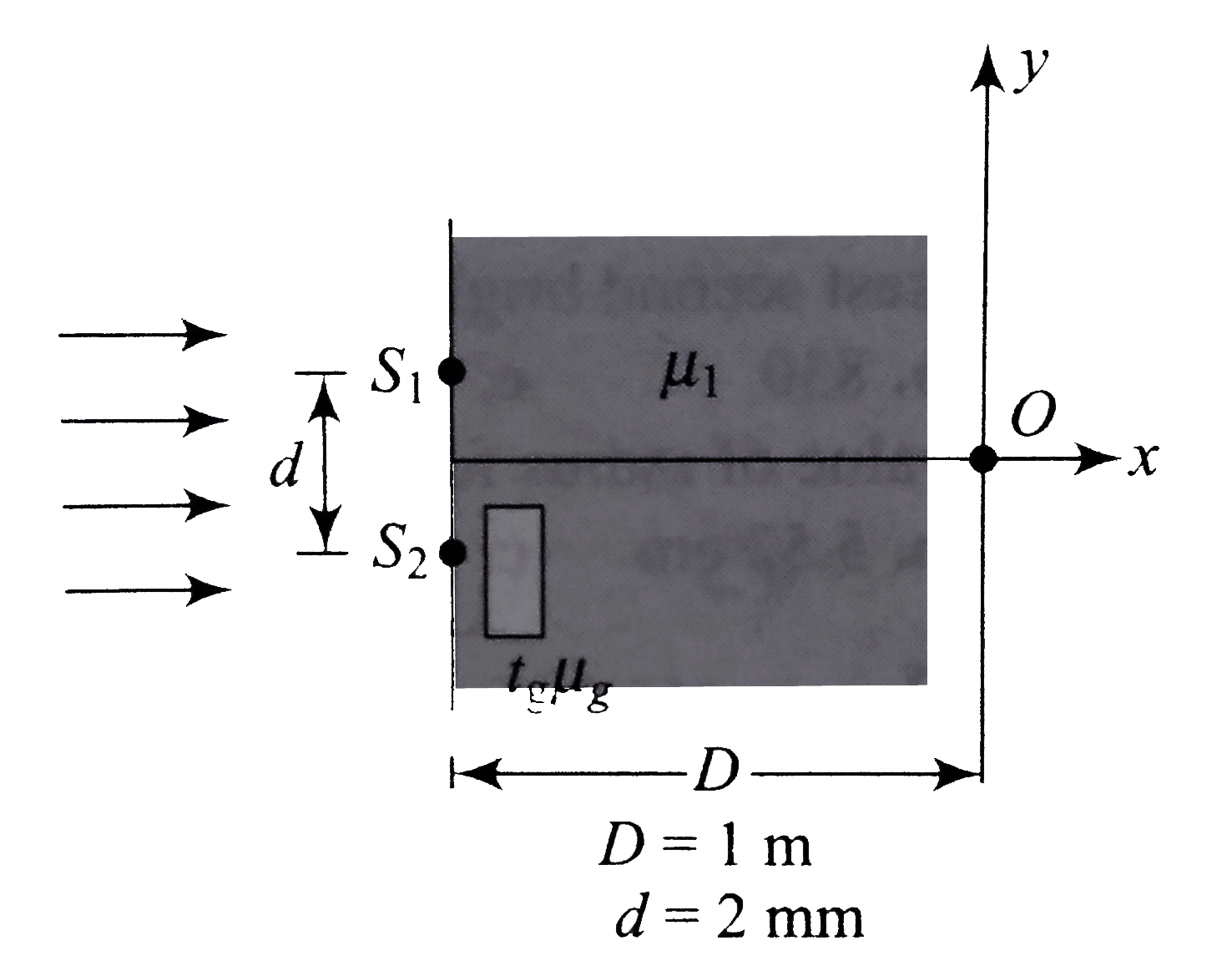
Find the time when central maxima is at point O. located symmetrically on the x-asix.
View Solution

