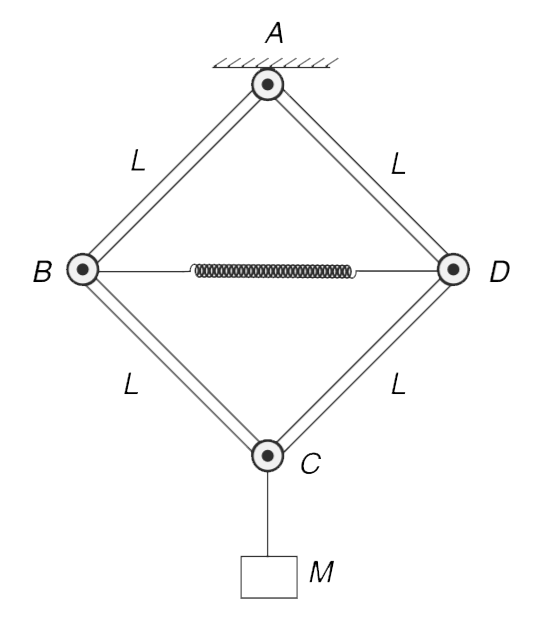
Four weightless rods of length l each are connected by hinged joints and form a rhomb (Fig). A hinge A is fixed, and a load is suspended to a hinge C. Hinges D and B are connected by a weightless spring of length 1.5l in the undeformed state. In equilibrium, the rods form angles α0=30∘ with the vertical. Determine the period T of small oscillations of the load.

Step by step video & image solution for Four weightless rods of length l each are connected by hinged joints and form a rhomb (Fig). A hinge A is fixed, and a load is suspended to a hinge C. Hinges D and B are connected by a weightless spring of length 1.5l in the undeformed state. In equilibrium, the rods form angles alpha_(0) = 30^(@) with the vertical. Determine the period T of small oscillations of the load. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Four identical mass less rods are connected by hinged joints to form a rhombus of side length L. Rods can rotate freely about the joints. The joints B and D are connected by a mass less spring of relaxed length 1.5 L. The system is suspended vertically with a load of mass M attached at C (see fig). In equilibrium the rods form an angle of 30∘ with the vertical. Find time period of small oscillations of the load.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
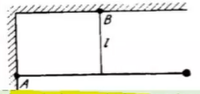
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View Solution
Knowledge Check
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
Amg/2B2mgCmg/2√3D√3mgFour rods of side length l have been hinged to form a rhombus. Vertex A is fixed to a rigid support, vertex C is being moved along the x-axis with constant velocity V as shown in figure. The rate at which vertex B is nearing the x-axis at the moment the rhombus is in the form of a squarem is
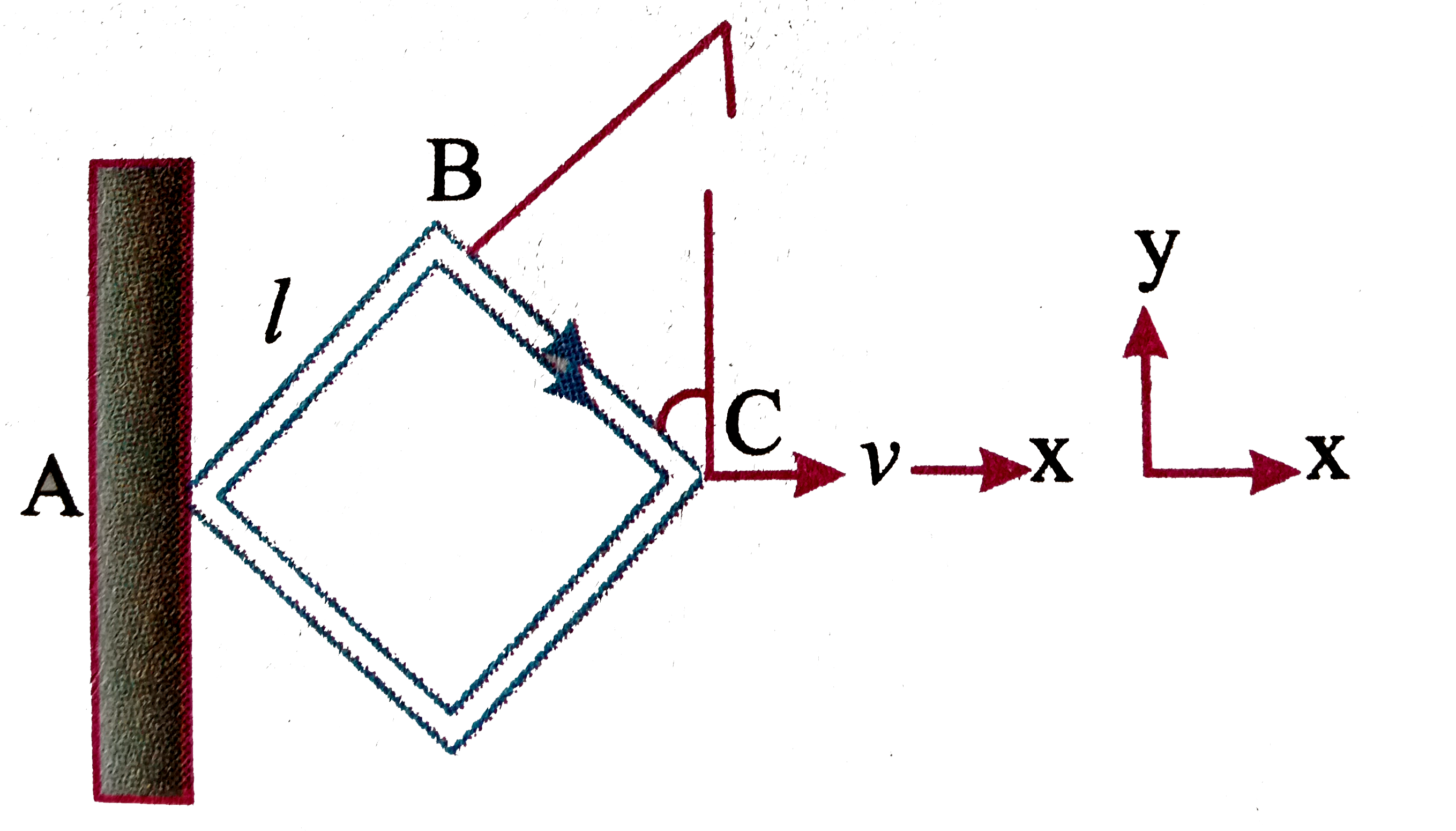 AV4BV√2CV2DV2g
AV4BV√2CV2DV2g
A weightless horizontal rigid rod along which two balls of the same mass m can move without friction rotates at a constant angular velocity ω about a vertical axle. The balls are connected by a weightless spring of rigidity k, whose length in the undeformed state is l0. The ball which is closer to the vertical axle is connected to it by he same spring. Determine the lengths of the springs. Under what conditions will be balls move in circles ?
View SolutionThree weightless rods of length 1 each are hinged at points A and B lying on the same horizontal and joint through hinges at points C and D (Fig. ). The length AB=2l. A load of mass m is suspended at the hinge C. Determine the minimum force Fmin aplied to the hinge D for which the middle rod remains horizontal.

View SolutionA weightless rod of length l with a small load of mass m at the end is hinged at point A (Fig.) and occupies a strictly vertical position, touching a body of mass M. A light jerk sets the system in motion . For what mass ratio M/m will the rod form an angle α=π/6 with the horizontal at the moment of the separation from the body ? What will be the velocity u of the body at this moment ? Friction should be neglected.

View SolutionA weightless rod of length l with a small load of mass m at the end is hinged at point A as shown and occupies a strictly vertical position, touching a body of mass M. A light jerk sets the system in motion.
a. For what mass ratio M/m will the rod form an angle α=π/6 with the horizontal at the moment of the separation from the body?
b. What will he the velocity u of the body at this moment? Friction should be neglected.

View Solution
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20cm, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form πX10s and fill the value of X.
View Solution
