A homogeneous rod of length 2l leans against a vertical wall at one end and against a smooth stationary surface at another end. What function y (.x) must be used to describe the cross section of this surface for the rod to remain in equilibrium in any position even in the absence of friction? Assume that the rod remains all the time in the same vertical plane perpendicular to the plane of the wall.
Step by step video & image solution for A homogeneous rod of length 2l leans against a vertical wall at one end and against a smooth stationary surface at another end. What function y (.x) must be used to describe the cross section of this surface for the rod to remain in equilibrium in any position even in the absence of friction? Assume that the rod remains all the time in the same vertical plane perpendicular to the plane of the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A rigid rod leans against a vertical wall (y-axis) as shwon in figure. The other end of the rod is ion the horizontal floor. Point A is pushed downwards with constant velocity. Path of the centre of the rod is

View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
Knowledge Check
A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
 AThe other end also moves uniformlyBThe speed of other end goes on decreasingCThe speed of other end goes on increasingDThe speed of other end first decreases and then increases
AThe other end also moves uniformlyBThe speed of other end goes on decreasingCThe speed of other end goes on increasingDThe speed of other end first decreases and then increasesA rod is hinged vertically at one end and is forced to oscillate in a vertical plane with hinged end at the top, the motion of the rod:
Ais simple harmonicBis oscillatory but not simple harmonicCis pericolic but not oscillatoryDmay be simple harmonicA uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
Aits center of mass moves vertically downwards on a straight lineBIts center of mass remains in restCthe rod rotates about a vertical axisDBoth a and c are correct
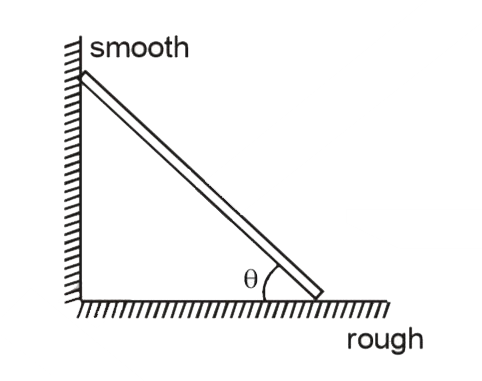
A stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
View SolutionA uniform thin rod of mass m and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbane at t = 0 causes the lower end t slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centr of mass of the rod during its fall?
(ii) Find the equaiton to the trajectory of a point on the rod shape of the path of this point?
View SolutionA brass rod of length 1m is fixed to a vertical wall at one end, with the other end keeping free to expand. When the temperature of the rod is increased by 120∘C, the length increases by 3cm. What is the strain?
View SolutionA smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?

View SolutionA unifrom rod of mass m and length l0 is pivoted at one end and is hanging in the vertical at one end and is hagingh in the vertical direction.The period of small angular oscillations of the rod is

View Solution
