One rope of a swing is fixed above the other rope by b. The distance between the poles of the swing is a. The lengths l1 and l2 of the ropes are such that l21+l22=a2+b2 (Fig ).
Determine the period T of small oscillations of the swing, neglecting the height of the swinging person in comparison with the above lengths.

Step by step video & image solution for One rope of a swing is fixed above the other rope by b. The distance between the poles of the swing is a. The lengths l_(1) and l_(2) of the ropes are such that l_(1)^(2) + l_(2)^(2) = a^(2) + b^(2) (Fig ). Determine the period T of small oscillations of the swing, neglecting the height of the swinging person in comparison with the above lengths. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is 1. Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log.
View SolutionThe distance between two points P and Q is d and the lengths of projections of PQ on the coordinate planes are l1,l2,l3 then l1+l22+l23d2
View Solution
Knowledge Check
Consider a swing whose one end is fixed above the other rope by ''b'. The distance between the poles of swing is a. The lengths l1 and l2 are such that l21+l22=a2+b2 as shown. The period of the smaller oscillations of the swing, by neglecting the height of the swinging person, is.....
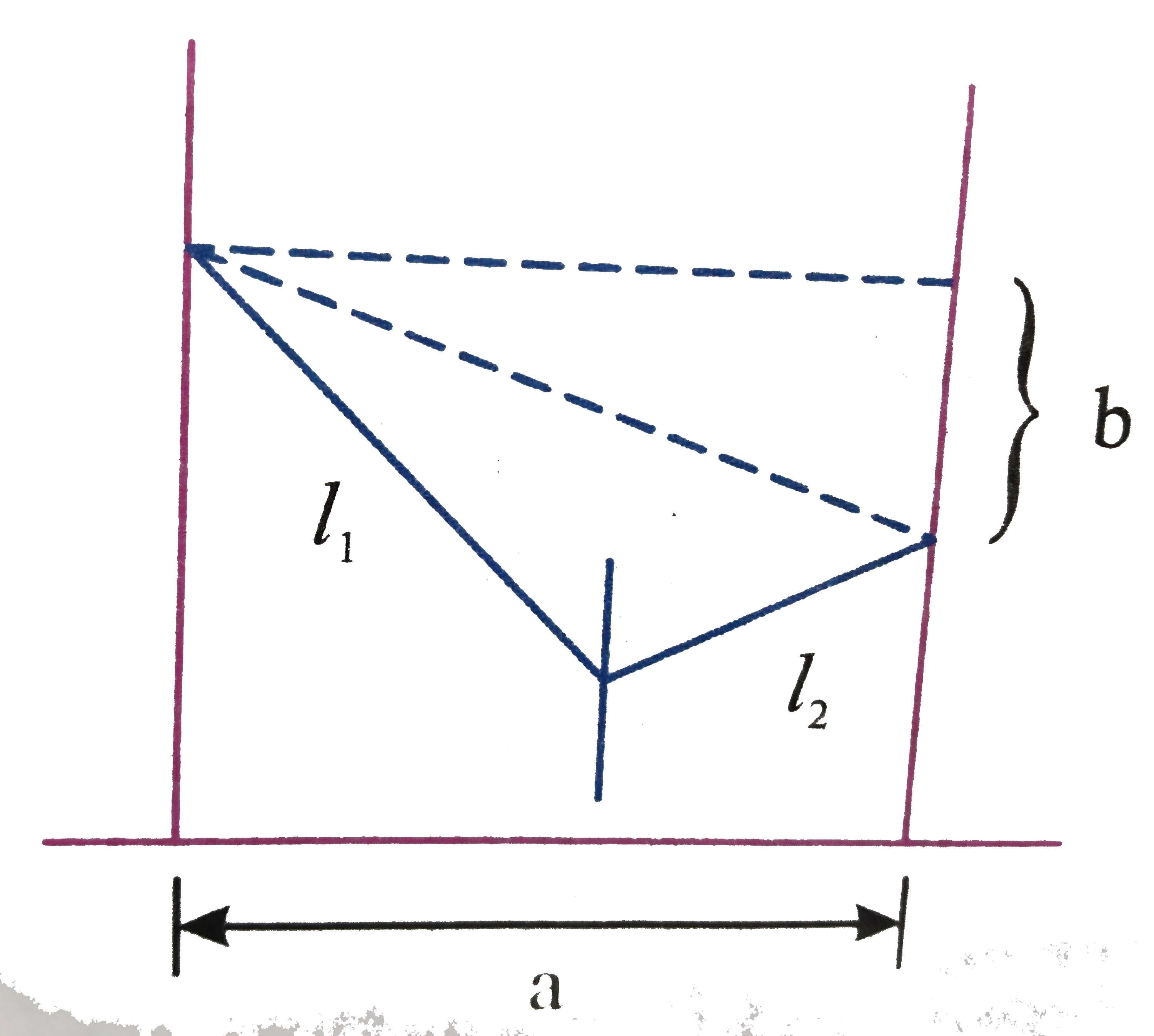 A2π√l1+l2gB2π√l1l2gaC2π√l1l2g(a+b)D2π ⎷l21+l22g(a+b)
A2π√l1+l2gB2π√l1l2gaC2π√l1l2g(a+b)D2π ⎷l21+l22g(a+b)Consider the line L 1 : x 1 y 2 z 1 312 +++ ==, L2 : x2y2z3 123
A0B17√3C413√3D175√3A spring has length l and force constant k it is cut into two springs of legnth l1 and l2 such that l1=nl2(n=an integer). Mass 'm' suspended form l1 oscillates with time period.
AT=2π√m(n+1)KBT=2π√nm(n+1)KCT=2π√mKDT=2π√(n+1)mK
If a rectangle has length L and the width is one-half of the length, then the area of the rectangle is (a) L (b) L2 (c) 12L2 (d) 14L2 (e) 2L
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View SolutionThe length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
View SolutionIf the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
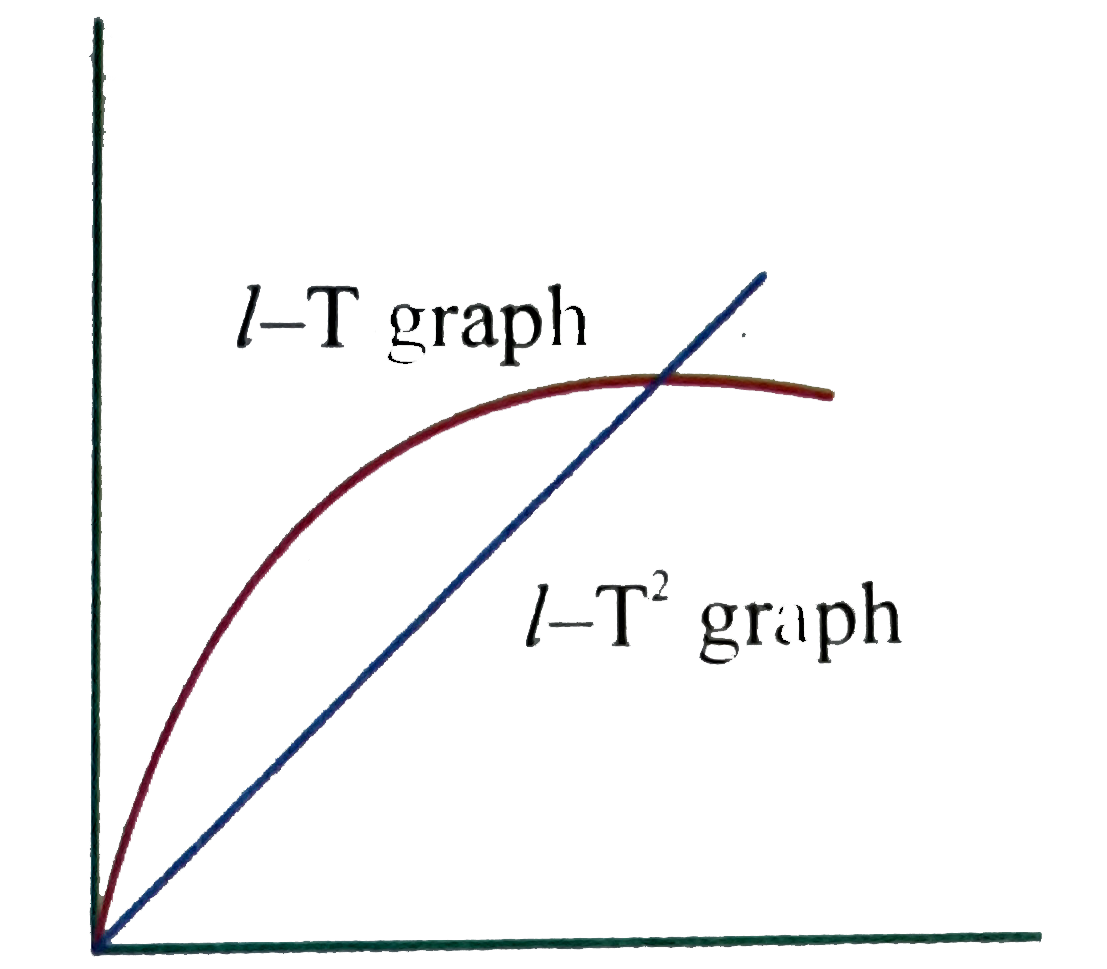
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View Solution
