A bead of mass m can move without friction along a long wire bent in a vertical plane in the shape of a graph of a certain function. Let lA be the length of the segment of the wire from the origin to a certain point A. It is knonw that if the bead is released at point A such that lA<lA0, its motion will be strictly harmonic l(t)=lAcosωt. Prove that there exists a point B(lA0<<lB) at which the condition of harmonicity of oscillations will be violated.
Step by step video & image solution for A bead of mass m can move without friction along a long wire bent in a vertical plane in the shape of a graph of a certain function. Let l_(A) be the length of the segment of the wire from the origin to a certain point A. It is knonw that if the bead is released at point A such that l_(A) lt l_(A_(0)), its motion will be strictly harmonic l (t) = l_(A) cos omega t. Prove that there exists a point B (l_(A_(0)) lt lt l_(B)) at which the condition of harmonicity of oscillations will be violated. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
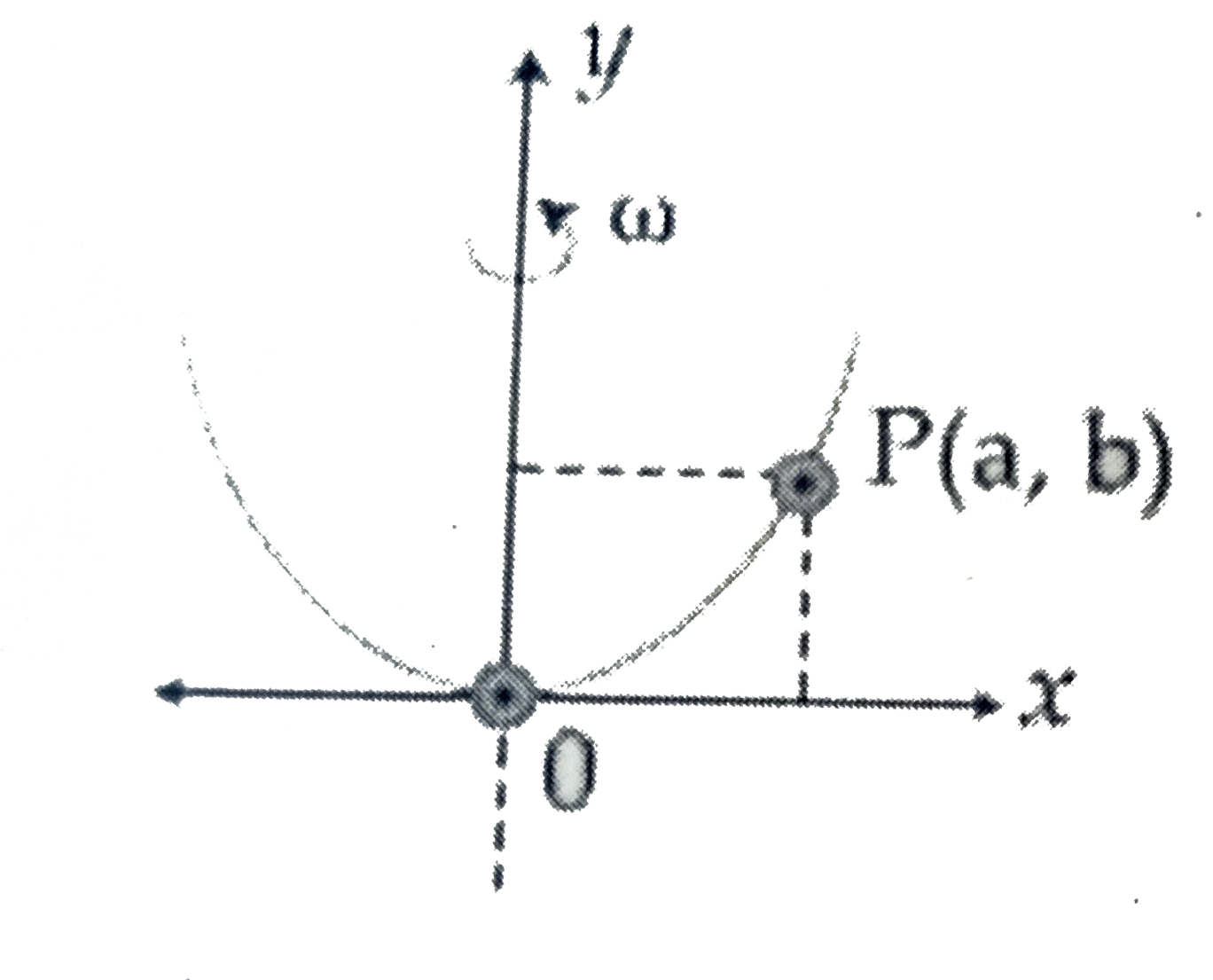
A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
View SolutionA steel wire of length l has a magnetic moment M. It is bent in L - shape (Figure). The new magnetic moment is

View Solution
Knowledge Check
A steel wire of length l has a magnetic moment M. It is bent in shape at its midpoint. The new magnetic moment is
AMBm√2CM2D2MA wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is
 AGmπl along x- axisBGmπl along y-axisC2pGml2 along y-axisD2πGml2 along x-axis
AGmπl along x- axisBGmπl along y-axisC2pGml2 along y-axisD2πGml2 along x-axisA steel wire of length l has a magnetic moment M. It is bent into L shape from the middle. The new magnetic moment is :
AMBM√2CM2D2M
A loop with current l Is in the field of a long straight wire with current l0.The plane of the loop is perpendicular to the straight wire.Find torque acting on the loop.

View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
View Solution
