A uniform sphere of radius R has a spherical cavity of radius R2 (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find:
(a) The kinetic energy of the sphere at this moment.
(b) The velocity of the centre of mass at this moment.
(c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing
![A uniform sphere of radius R has a spherical cavity of radius (R)/(2) (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find: (a) The kinetic energy of the sphere at this moment. (b) The velocity of the centre of mass at this moment. (c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C06_E01_124_Q01.png)
The correct Answer is:(a) 3140MV2
(b) 15V14
(c) V≤√1415gR
Step by step video, text & image solution for A uniform sphere of radius R has a spherical cavity of radius (R)/(2) (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find: (a) The kinetic energy of the sphere at this moment. (b) The velocity of the centre of mass at this moment. (c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
There is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric field (magnitude only) at the center of the cavity will be :
View Solution
Knowledge Check
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
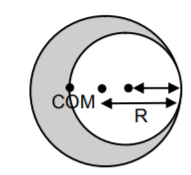A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1A solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
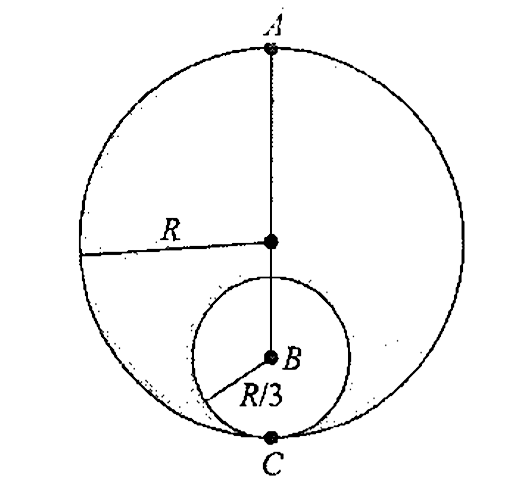AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
View SolutionA solid sphere of radius R has a concentric cavity of radius 'R/2' inside it. The sphere is found to just float in water with the highest point of it touching the water surface. The specific gravity of the material of the sphere is
View Solution