A solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
+Q,−Q
−Q,+Q
Q,−Q
+Q,0
The correct Answer is:B
To solve the problem, we need to analyze the situation of a solid spherical conductor with a spherical cavity at its center, where a charge +q is placed at the center of the cavity. We will determine the charge on the inner and outer surfaces of the conductor.
1. Understanding the Setup:
- We have a solid spherical conductor with radius R.
- There is a spherical cavity of radius r at the center of this conductor.
- A charge +q is placed at the center of the cavity.
2. Electric Field Inside the Conductor:
- In electrostatics, the electric field inside a conductor in electrostatic equilibrium is zero. This means that there cannot be any electric field present in the material of the conductor itself.
3. Induced Charge on the Inner Surface:
- Since there is a charge +q at the center, it will induce a charge on the inner surface of the cavity.
- To neutralize the electric field due to the charge +q within the conductor, an equal and opposite charge must be induced on the inner surface of the cavity.
- Therefore, the charge induced on the inner surface of the cavity will be −q.
4. Total Charge on the Conductor:
- The conductor as a whole must remain electrically neutral. If we denote the total charge of the conductor as Q, we have:
Q=Qinner+Qouter
- Since the inner surface has a charge of −q, we can express this as:
Q=−q+Qouter
- For the conductor to be neutral, if Q is zero (assuming the conductor was initially uncharged), then:
0=−q+Qouter
- This leads to:
Qouter=+q
5. Final Charges:
- The charge on the inner surface of the cavity is −q.
- The charge on the outer surface of the conductor is +q.
Conclusion:
- The charge on the inner surface is −q.
- The charge on the outer surface is +q.
- We have a solid spherical conductor with radius R.
- There is a spherical cavity of radius r at the center of this conductor.
- A charge +q is placed at the center of the cavity.
- In electrostatics, the electric field inside a conductor in electrostatic equilibrium is zero. This means that there cannot be any electric field present in the material of the conductor itself.
- Since there is a charge +q at the center, it will induce a charge on the inner surface of the cavity.
- To neutralize the electric field due to the charge +q within the conductor, an equal and opposite charge must be induced on the inner surface of the cavity.
- Therefore, the charge induced on the inner surface of the cavity will be −q.
- The conductor as a whole must remain electrically neutral. If we denote the total charge of the conductor as Q, we have:
Q=Qinner+Qouter
- Since the inner surface has a charge of −q, we can express this as:
Q=−q+Qouter
- For the conductor to be neutral, if Q is zero (assuming the conductor was initially uncharged), then:
0=−q+Qouter
- This leads to:
Qouter=+q
- The charge on the inner surface of the cavity is −q.
- The charge on the outer surface of the conductor is +q.
- The charge on the inner surface is −q.
- The charge on the outer surface is +q.
Similar Questions
A solid spherical conductor of radius R has a spherical cavity of radius a(a+Q is kept at the center.The charge at the inner surface outer and at a position r(a<r<R)are respectively.
View SolutionA solid spherical conductor of radius R has a spherical cavity inside it (see figure). A point charge q is placed at the centre of the cavity. (a) What is the potential of the conductor? (b) If the charge q is shifted inside the cavity by a distance Δx, how does the potential of the conductor change? (c) How does your answer to the question (a) and (b) change if the cavity is not spherical and the charge q is placed at any point inside it (see figure) (d) Draw electric field lines in entire space in each case. In which case all field lines are straight lines
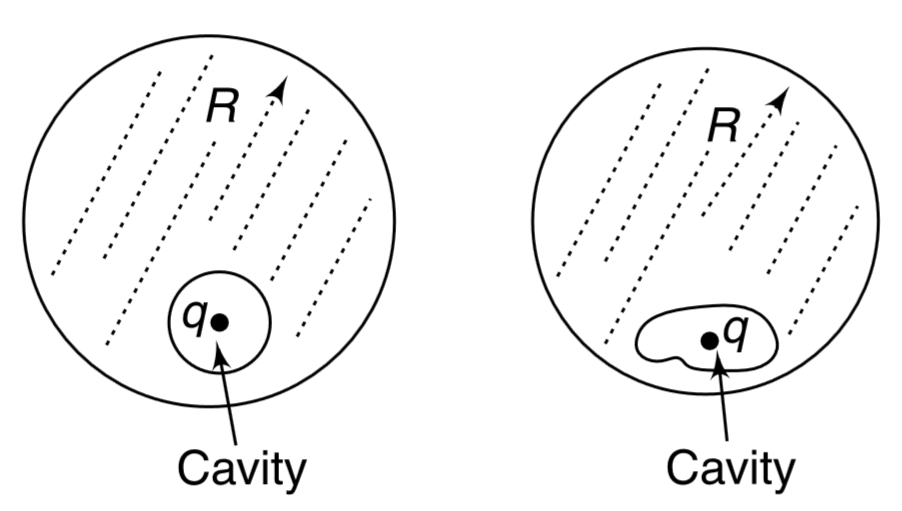
View Solution
Knowledge Check
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1A metallic ball has spherical cavity at its centre. If the ball is heated, what happens to the cavity
AIts volume decreases.BIts volume remains constant.CIts volume increases.DNothing can be decided.A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
A charge q is placed at the centre of the shell. Find out the surface charge density on the inner and outer surface of the shell.
Is the electric field inside a cavity (with no charge ) zero. Independent of the fact wheather the shell is spherical or not ? Explain.
View SolutionA spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is

View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA spherical body of radius 'b' has a concentric cavity of radius 'a' as shown. Thermal conductivity of the material is K. Find thermal resistance between inner surface P and outer surface Q.

View Solution
