A solid sphere of radius R has a concentric cavity of radius 'R//2' in

Inside a uniform sphere of mass M and radius R, a cavity of radius $R / 3$ , is made in the sphere as shown :

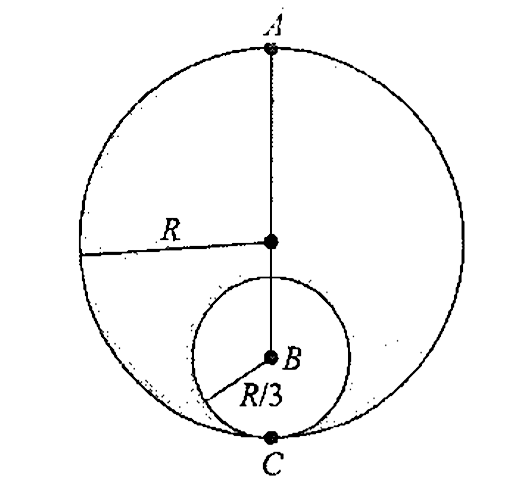AGravitational field inside the cavity is uniform
BGravitational field inside the cavity is non-uniform
CThe escape velocity of a particle projected from point A is $\sqrt{\frac{88 G M}{15 R}}$
DEscape velocity is defined for earth and particle system only
A conducting sphere of radius r has a charge . Then .
Athe charge is uniformly distributed over its surface if there is an external electric field .
BDistribution of charge over its surface will be non uniform if no external electric field exist in space,
CElectric field strength inside the sphere will be equal to zero only when no external electric field exists
DPotential at every point of the sphere must be same
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
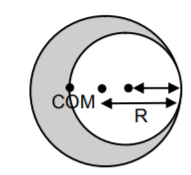A $(R^{2} + R + 1) (2 - R) = 1$
B $(R^{2} - R - 1) (2 - R) = 1$
C $(R^{2} - R + 1) (2 - R) = 1$
D $(R^{2} + R - 1) (2 - R) = 1$

A solid sphere of radius $R$ has a concentric cavity of radius ' $R / 2$ ' inside it. The sphere is found to just float in water with the highest point of it touching the water surface. The specific gravity of the material of the sphere is