A hollow sphere of external radius R and thickness t (< < R) is made of a metal of density ρ. The sphere will float in water if
t≤Rρ
t≤R3ρ
t≤R2ρ
t≥R3ρ
The correct Answer is:B
To solve the problem of whether a hollow sphere of external radius R and thickness t will float in water, we need to analyze the conditions for flotation based on the principles of buoyancy and density.
1. Understand the Condition for Floating:
A hollow sphere will float if the weight of the sphere is less than or equal to the weight of the water displaced by the volume of the sphere. This can be expressed mathematically using the principle of buoyancy.
2. Calculate the Volume of the Hollow Sphere:
The volume V of the hollow sphere can be calculated using the formula for the volume of a sphere. The volume of the outer sphere (with radius R) minus the volume of the inner sphere (with radius R−t) gives us the volume of the hollow part:
V=43πR3−43π(R−t)3
Simplifying this, we get:
V=43π(R3−(R−t)3)
3. Calculate the Mass of the Hollow Sphere:
The mass M of the hollow sphere can be calculated using the density ρ of the metal and the volume V:
M=ρ⋅V
4. Weight of the Hollow Sphere:
The weight of the hollow sphere Ws is given by:
Ws=M⋅g=ρ⋅V⋅g
where g is the acceleration due to gravity.
5. Weight of the Water Displaced:
The weight of the water displaced Ww when the sphere is submerged is given by the weight of the volume of water equal to the volume of the sphere:
Ww=Volume of water displaced⋅Density of water⋅g=V⋅ρw⋅g
where ρw is the density of water (approximately 1g/cm3 or 1000kg/m3).
6. Set Up the Inequality for Floating:
For the sphere to float, we need:
Ws≤Ww
This implies:
ρ⋅V⋅g≤V⋅ρw⋅g
Dividing both sides by V⋅g (assuming V≠0):
ρ≤ρw
7. Relate Density, Thickness, and Radius:
Since the thickness t is much smaller than the radius R, we can approximate the volume of the hollow sphere. The mass of the hollow sphere can be approximated as:
M≈4πR2t⋅ρ
The volume of the outer sphere is:
V≈43πR3
Setting the mass of the sphere less than or equal to the mass of the displaced water gives:
4πR2t⋅ρ≤43πR3⋅ρw
Simplifying this leads to:
t⋅ρ≤R⋅ρw3
8. Final Condition:
Rearranging gives us the condition for the thickness t:
t≤R⋅ρw3⋅ρ
Conclusion:
The hollow sphere will float in water if the thickness t is less than or equal to R⋅ρw3⋅ρ.
A hollow sphere will float if the weight of the sphere is less than or equal to the weight of the water displaced by the volume of the sphere. This can be expressed mathematically using the principle of buoyancy.
The volume V of the hollow sphere can be calculated using the formula for the volume of a sphere. The volume of the outer sphere (with radius R) minus the volume of the inner sphere (with radius R−t) gives us the volume of the hollow part:
V=43πR3−43π(R−t)3
Simplifying this, we get:
V=43π(R3−(R−t)3)
The mass M of the hollow sphere can be calculated using the density ρ of the metal and the volume V:
M=ρ⋅V
The weight of the hollow sphere Ws is given by:
Ws=M⋅g=ρ⋅V⋅g
where g is the acceleration due to gravity.
The weight of the water displaced Ww when the sphere is submerged is given by the weight of the volume of water equal to the volume of the sphere:
Ww=Volume of water displaced⋅Density of water⋅g=V⋅ρw⋅g
where ρw is the density of water (approximately 1g/cm3 or 1000kg/m3).
For the sphere to float, we need:
Ws≤Ww
This implies:
ρ⋅V⋅g≤V⋅ρw⋅g
Dividing both sides by V⋅g (assuming V≠0):
ρ≤ρw
Since the thickness t is much smaller than the radius R, we can approximate the volume of the hollow sphere. The mass of the hollow sphere can be approximated as:
M≈4πR2t⋅ρ
The volume of the outer sphere is:
V≈43πR3
Setting the mass of the sphere less than or equal to the mass of the displaced water gives:
4πR2t⋅ρ≤43πR3⋅ρw
Simplifying this leads to:
t⋅ρ≤R⋅ρw3
Rearranging gives us the condition for the thickness t:
t≤R⋅ρw3⋅ρ
The hollow sphere will float in water if the thickness t is less than or equal to R⋅ρw3⋅ρ.
Topper's Solved these Questions
- BULK PROPERTIES OF MATTERBOOK - MTG-WBJEECHAPTER - BULK PROPERTIES OF MATTEREXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (ONE OR MORE THAN ONE OPTION CORRECT TYPE)
1 Videos
- BULK PROPERTIES OF MATTERBOOK - MTG-WBJEECHAPTER - BULK PROPERTIES OF MATTEREXERCISE - WB JEE WORKOUT (ONE OR MORE THAN ONE OPTION CORRECT TYPE )
10 Videos
- ATOMS MOLECULES AND CHEMICAL ARITHEMETIC BOOK - MTG-WBJEECHAPTER - ATOMS MOLECULES AND CHEMICAL ARITHEMETIC EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS CATEGORY 1: SINGLE OPTION CORRECT TYPE (1 MARK)
3 Videos
- CURRENT ELECTRICITY BOOK - MTG-WBJEECHAPTER - CURRENT ELECTRICITY EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
21 Videos
Similar Questions
A hollow metal sphere of external radius 2cm, thickness t, just sinks in water. Find the value of t in centimetre. Given specififc gravity of metal is 2.5.
View SolutionThe radius of a solid iron sphere is 8 cm. Eight rings of iron plate of external radius cm and thickness 3 cm are made by melting this sphere. Find the internal diameter of each ring,
View Solution
Knowledge Check
A solid sphere of radius R and a hollow sphere of inner radius R/2 and outer radius R, made of copper ,are heated to the same temperature and are allowed to cool in the same environment .Then
Ahollow spehere cools fasterBboth the sphre attain room temperature at the same timeCsolid sphere cools fasterDnone of theseA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
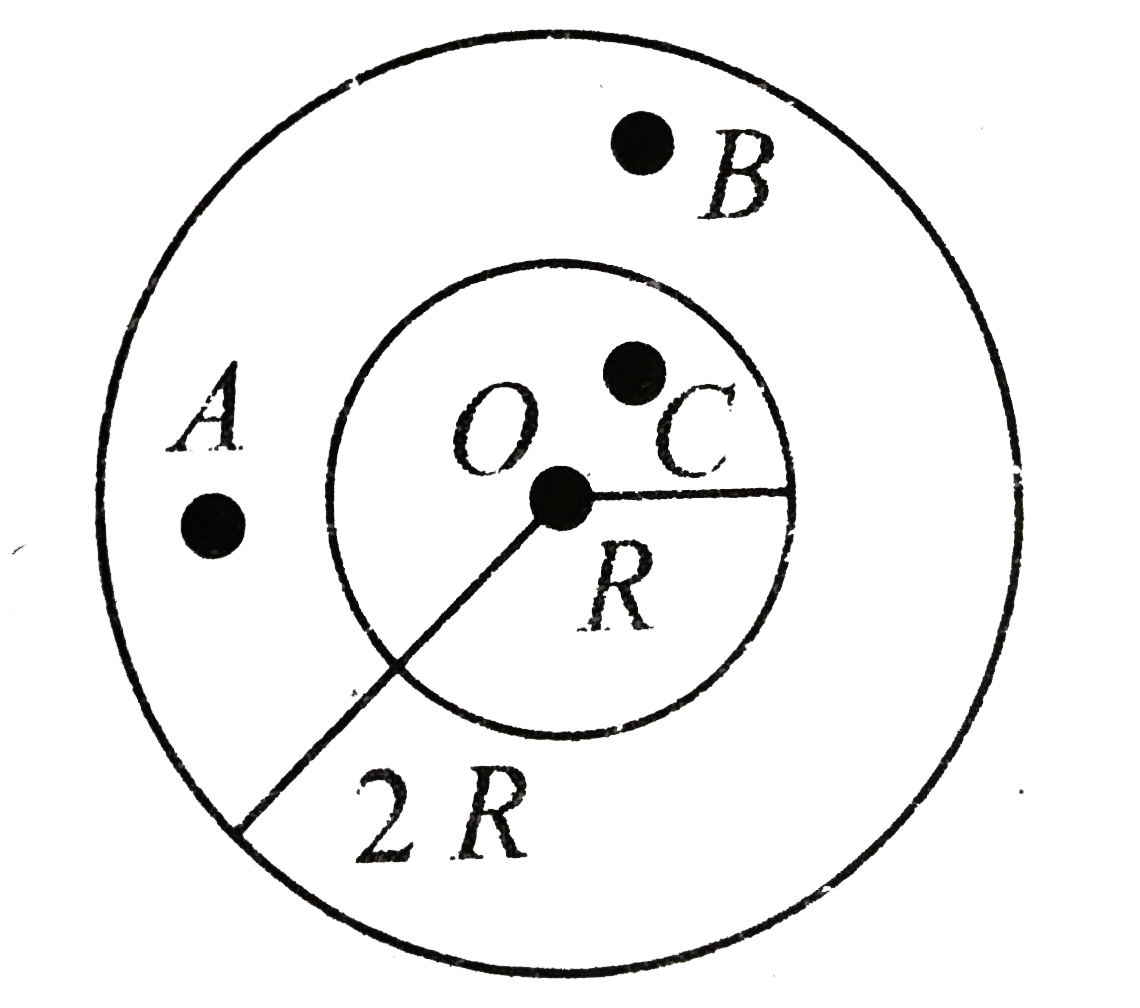 Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.
Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.A solid sphere of copper of radius R and hollow sphere of copper of inner radius r and outer radius R are heated to the same temperature and allowed to cool in the same environment. The rate of cooling is
Amore for hollow sphereBmore for solid sphereCsame for both the sphereDcan not say
The inner curved surface area of a hollow hemispherical bowl of external radius 14 cm and thickness 2 cm is ______.
View SolutionThe radius of a solid iron sphere is 8 cm. Eight rings of iron plate of external radius 623 cm and thickness 3 cm are made by melting this sphere. Find the internal diameter of each ring.
View SolutionA solid conducting sphere holds more charge than a hollow sphere of the same radius when they are at same potential.
View SolutionA metal ball of radius R is placed concentrically inside hollow metal sphere of inner radius 2R and outer radius 3R.The ball is given a charge +2Q and the hollow sphere a total charge −Q .The electrostatic potential energy of this system is
View SolutionThe moment of inertia of hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is
View Solution
