A hemispherical bowl of radius R is placed upside down on a flat horizontal surface. There is a small hole at the top of the inverted bowl. Through the hole, a liquid of density ρ is poured in. Exactly when the container gets full, water starts leaking from between the table and the edge of the container. Find the mass (m) of the contaienr.
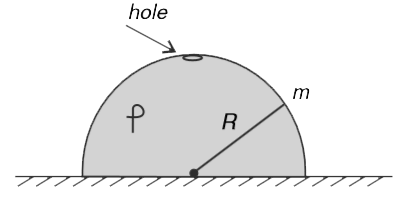
The correct Answer is:m=πR3ρ3
Step by step video, text & image solution for A hemispherical bowl of radius R is placed upside down on a flat horizontal surface. There is a small hole at the top of the inverted bowl. Through the hole, a liquid of density rho is poured in. Exactly when the container gets full, water starts leaking from between the table and the edge of the container. Find the mass (m) of the contaienr. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A hollow hemispherical bowl of mass m radius R is placed on a smooth horizontal surface. A particle (also of mass m) strikes the hemi spherical bowl at point P and sticks to it. the velocity of particle just after the collision in vertically upwards direction is ku25, where k is an integer. Find k.

View SolutionConsider a cuboidal vessel (2R×2R×R) with as hemispherical cavity of radius R, kept at a horizontal smooth surface as shown in the figure. The vessel has very small hole of cross-sectional area "a". Now water of density ρ is poured into space developed due horizontal surface adn vessel through hole very slowly. When the height of waer level is h, the vessel lifts off the surface and liquid leaks through space generated. (R=2m,ρ=103kg/m3,m=9πkg). If the value of h is 5kcm, find the value of k.
(Atmospheric pressure =105N/m2).

View Solution
Knowledge Check
A container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case
 Aboth a and v depend on hBonly a depends on hConly v depends on hDneither a nor v depends on h
Aboth a and v depend on hBonly a depends on hConly v depends on hDneither a nor v depends on h
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)A(2/3)πR2hρgB(1/3)πR2hρgCπR2hρgDNone
An air puck of mass m1 is tied to a string allowed to revolved in a circle of radius R on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass m2 is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the monsion of the puck if the value of m2 is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the monsion of the puck if the value of m2 is instead decreased removing a part from the hanging load.
View SolutionFigure shows a body A at the top of a frictionless hemispherical inverted bowl of radius R. If the body starts slipping from the highest point, then the horizontal distance between the point where it leaves contact with sphere and the point at which the body was placed is

View SolutionA hemisphere of radius R and of mass 4m is free to Slide with its base on a smooth horizontal table. A particle mass m is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement θ when velocity of hemisphere has become v.

View SolutionA spherical fish bowl of radius R is placed in front of a plane vertical mirror (M) The thickness of the wall of the fish bowl is very thin The centre (C) of the spherical bowl is at distance of 3R from the plane mirror. The bowl is filled with water and contains a fish (F) Fish(F) is at a distance of R from the centre of the spherical bowl as shown in the figure Refractive index of water is 4/3 two surfaces are indicated in the bowl as first surface (1) and second surface(2)

Column-IColumn-IIOptical Event–––––––––––––––Nature of image––––––––––––––––––(A)Refraction at first surface(P)Virtual(B)Refraction at second surface after reflection from mirror(Q)Real(C)Refraction at first surface after reflectionfrom mirror and refraction from second surface(R)Magnified(S)Diminished
View Solution(i) In the arrangement shown in the figure, the tank has a large cross section and the pipes have much smaller cross section. The opening at A is unplugged and the water jet hits the ground surface at a horizontal distance x.
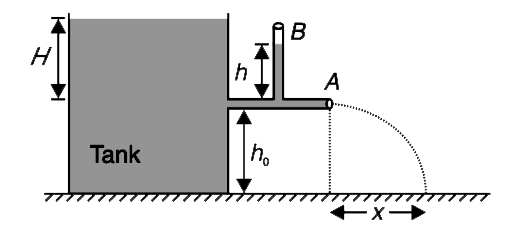
(a) Find the level of water (h) in the tube B as water flows out of A.
(b) Find x.
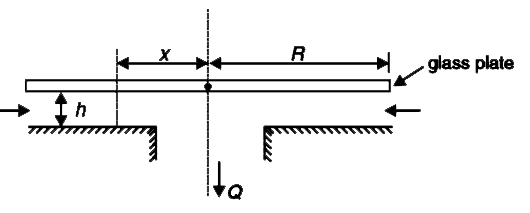
(i) A flat horizontal surface has a small hole at its centre . A circular glass plate of radius R is placed symmetrically above the hole with a small gap h remainng between the plate and the surface A liquid enters the gap symmetrically from all sides and after travelling radially through the gap finally exits from the hole. The volume flow rate of the liquid coming out from the hole is Q (in m3s−1).
(a) If the flow speed just inside the circumference of the circular plate is V0 and the speed (Vx) of flow inside the gap at distance x(see figure) from the centre of the hole.
(b) Write Vx in terms of Q, h and x.
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View Solution