Consider a cuboidal vessel (2R×2R×R) with as hemispherical cavity of radius R, kept at a horizontal smooth surface as shown in the figure. The vessel has very small hole of cross-sectional area "a". Now water of density ρ is poured into space developed due horizontal surface adn vessel through hole very slowly. When the height of waer level is h, the vessel lifts off the surface and liquid leaks through space generated. (R=2m,ρ=103kg/m3,m=9πkg). If the value of h is 5kcm, find the value of k.
(Atmospheric pressure =105N/m2).

The correct Answer is:6
mg=FB=[πR2h−∫h0π(R2−z2)dz]ρg⇒m=πh3ρ3
⇒h3=3mπρ=3×π×9π×103⇒h=310=0.3m=30m
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
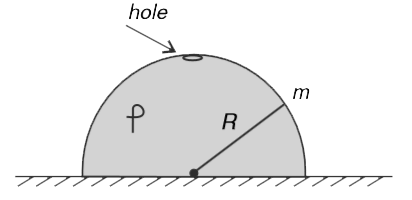
A hemispherical bowl of radius R is placed upside down on a flat horizontal surface. There is a small hole at the top of the inverted bowl. Through the hole, a liquid of density ρ is poured in. Exactly when the container gets full, water starts leaking from between the table and the edge of the container. Find the mass (m) of the contaienr.
View SolutionA light cylindrical vessel is kept on a horizontal surface. Its base area is A. a hole of cross sectional area a is made just at its bottom side (where a less than A). Find minimum coefficeint of friction necessary for sliding of the vesssel due to the impact force of the emerging liquid.

View Solution
Knowledge Check
A light cylindrical vessel is kept on a horizontal surface it's base area is A. A hole of cross-sectional area a is made just at it's bottom side. The minimum coefficient of friction necessary for not sliding of vessel dueto the impact force of the emerging liquid.
AvaryingBaAC2aADnoneFigure here shows the vertical cross-section of a vessel filled with a liquid of density ρ. The normal thrust per unit area on the walls vessel at point. P, as shown, will be
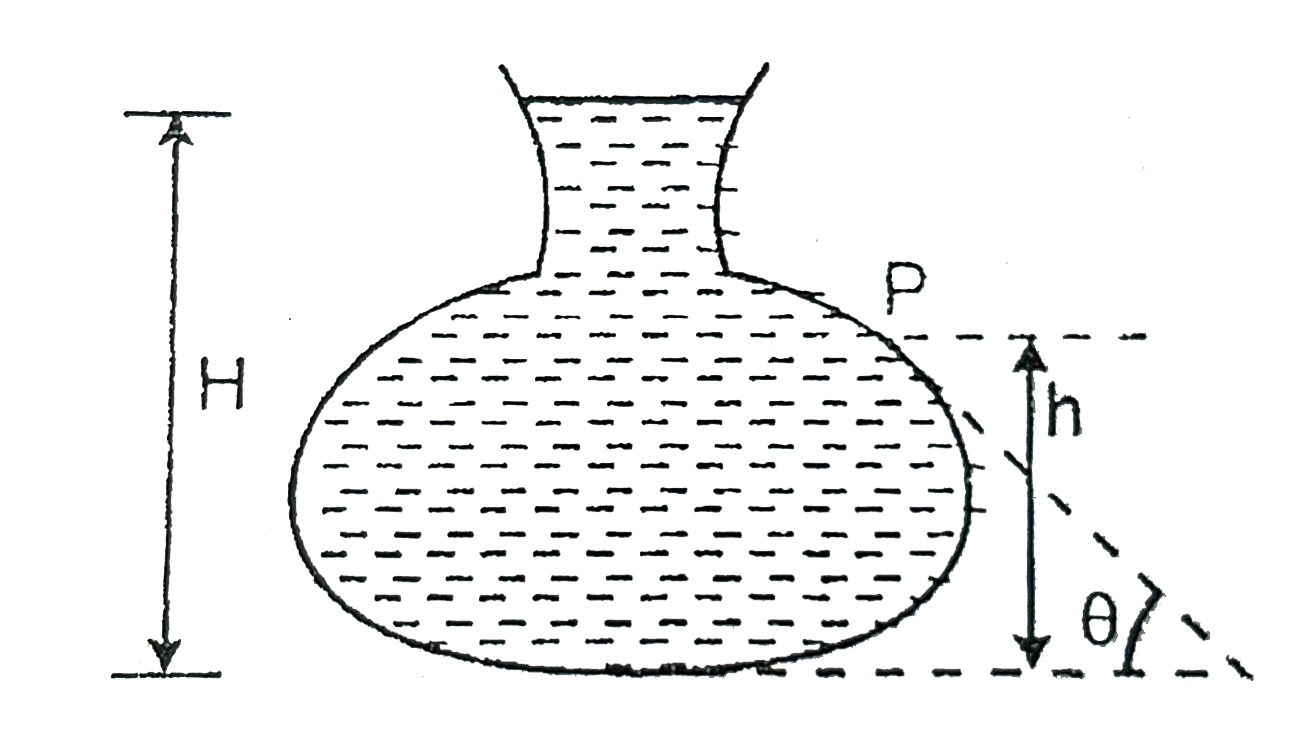 AhρgBHρgC(H−h)ρgD(H−h)ρgcosθ
AhρgBHρgC(H−h)ρgD(H−h)ρgcosθA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
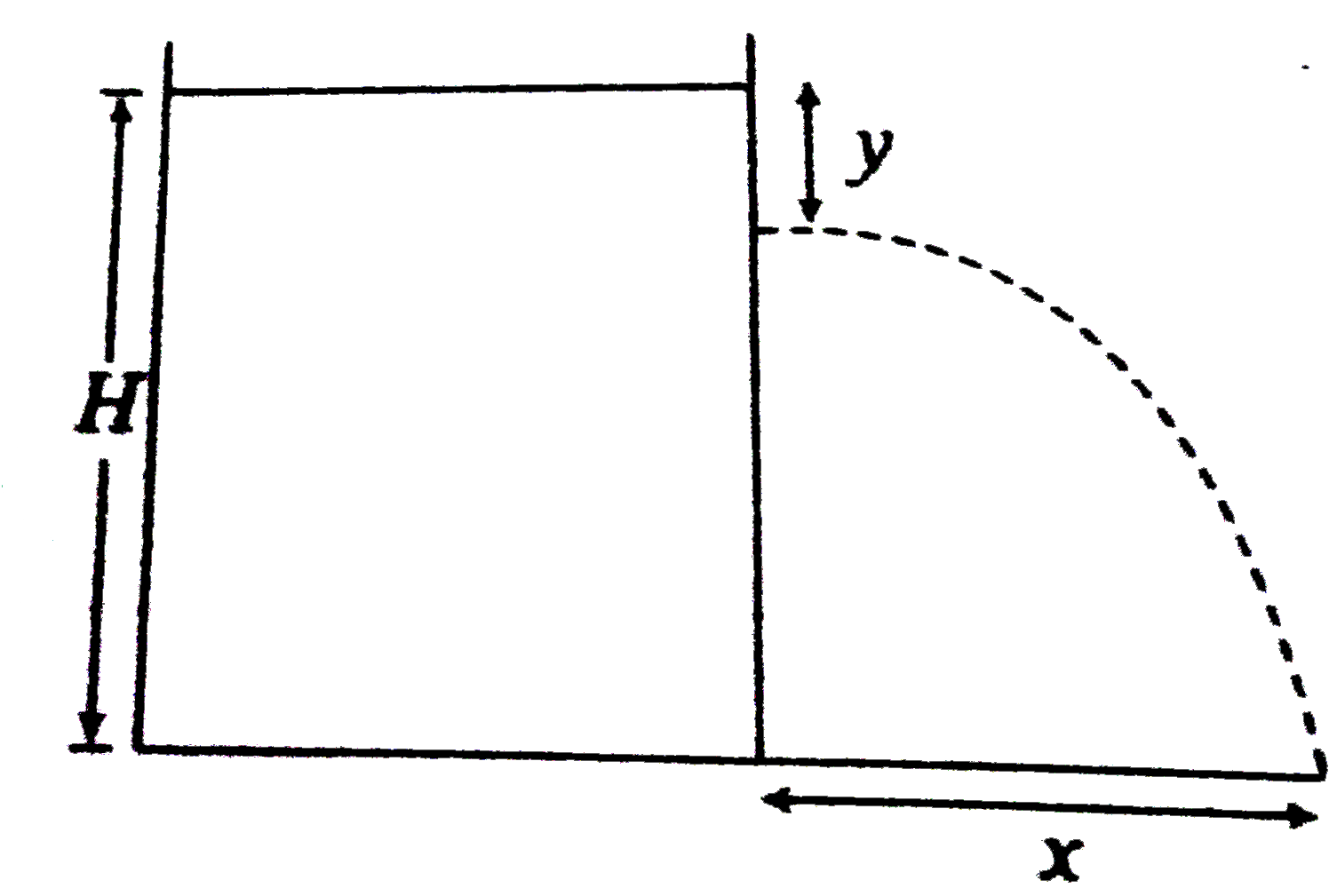 Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
A light cylindrical vessel is kept on a horizontal surface. Its base area is A. a hole of cross sectional area a is made just at its bottom sdie (where a ltlt A). Find minimum coefficeint of friction necessary for sliding of the vesssel due to the impact force of the emerging liquid.

View SolutionWater is poured to same level in each of the vessels shown in the figure , all having the same base area . In which vessel is the force experienced by the base maiximum ?

View SolutionIf water is ejecting from a hole of radius r at a depth h from the water surface in cylindrical vessel of diameter D, then speed with which the water level in the vessel drops .(Consider area of hole is comparable to area of vessel)
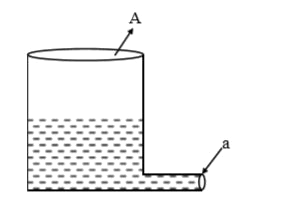
View SolutionA light cylindrical vessel is kept on a horizontal surface. Area of base is A. A hole of crosssectional area 'a' is made just at its bottom side. The minimum coefficient of friction necessary to prevent sliding the vessel due to the impact force of the emerging liquid is (a<<A):
View SolutionA cyclinderical vessel of cross-sectional area 1000cm2, fitted with a frictonless piston of mass 10kg, and filled with water completely. A small hole of cross-sectional area 10mm2 is opened at a point 50cm deep from the lower surface of the piston. The velocity of efflux from the hole will be
View Solution

