Consider a wave sent down a string in the positive direction whose equation is given is
$y = y_{0} sin [ω (t - \frac{x}{v})]$
The wave is propagated along because each string segment pulls upward and downward on the segment adjacent to it a slightly larger value of $x$ and, as a result does work upon the string segment to which wave is travelling.
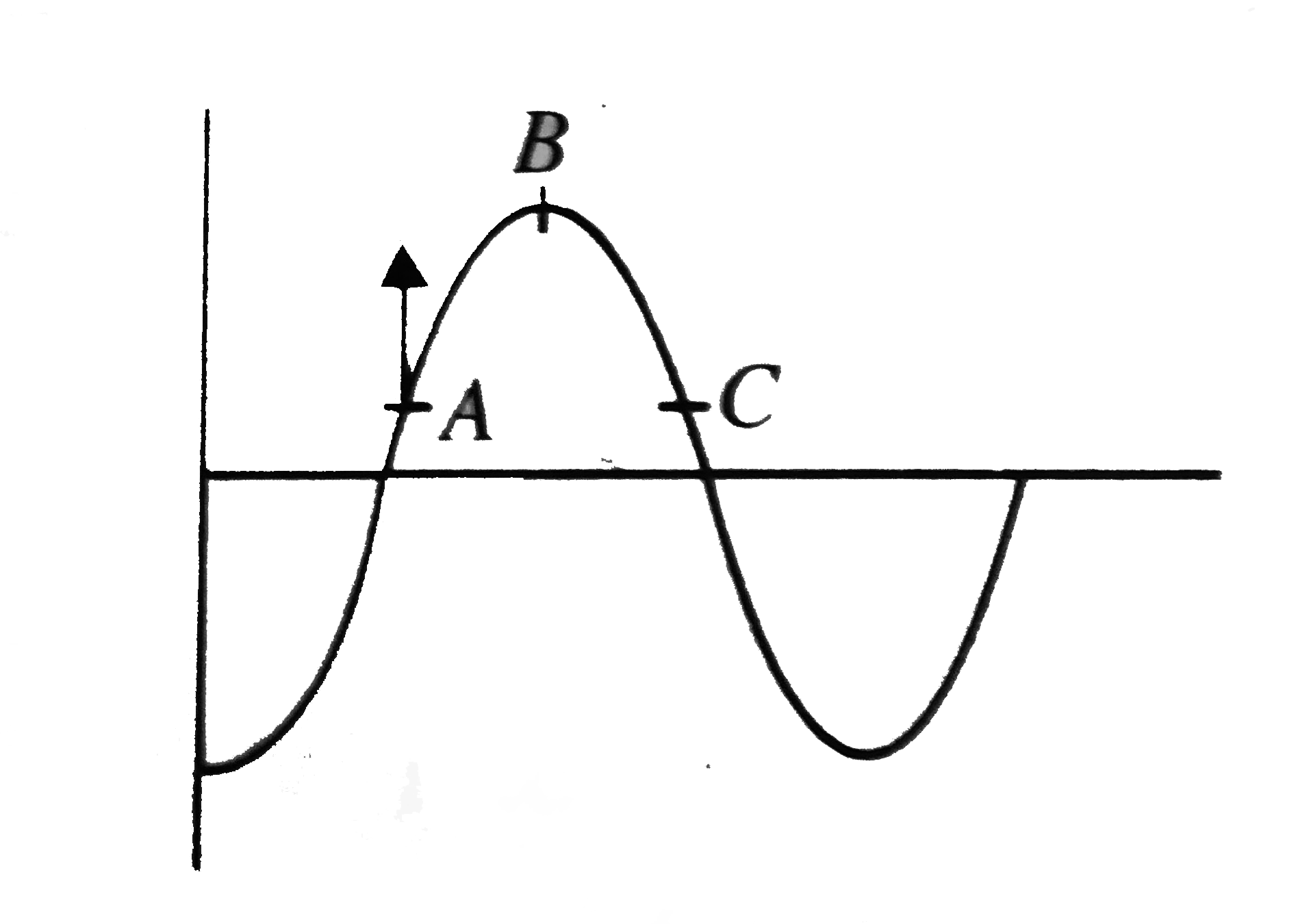
For example, the portion of string at point $A$ is going upward, and will pull the portion at point $B$ upward as well. In fact, at any point along the string, each segment of the string is pulling on the segment just adjacent and to its right, causing the wagve to propagate. It is by this process that the energy is sent along the string.
Now we try to calculate how much energy is propagated down the stirng per second
$T_{y} = t sin θ \approx T tan θ \Rightarrow T_{y} = - T \frac{\partial y}{\partial x}$
(The negative sign appears because as shown in the figure II, the slope is negative) the force will act through a distance
$d y = v_{y} d t = \frac{\partial y}{\partial t} d t$
Therefore work done by force in time $d t$ is
$d W = T_{y} d y = - T (\frac{\partial y}{\partial x}) (\frac{\partial y}{\partial t}) d t \Rightarrow d W = \frac{ω^{2} y_{0}^{2} T}{v} {cos}^{2} [ω (t - \frac{x}{V})] d t$ .....(A)

The average power transmitted down the string (i.e. the average energy transfer or sent down it per second) is

$\frac{2 ω^{2} y_{0}^{2} T}{v}$

$\frac{ω^{2} y_{0}^{2} T}{v}$

$\frac{ω^{2} y_{0}^{2} T}{2 v}$

$\frac{ω^{2} y_{0}^{2} T}{4 v}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

During one time period $(T_{0})$
$W = \frac{T ω^{2} y_{0}^{2}}{2 v} [\int_{0}^{T_{0}} (1 + cos {2 ω (t - \frac{x}{v})}) d t]$
Average Power $= \frac{W}{T_{0}} = \frac{ω^{2} y_{0}^{2} T}{2 V}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Consider a wave sent down a string in the positive direction whose equation is given is
$y = y_{0} sin [ω (t - \frac{x}{v})]$
The wave is propagated along because each string segment pulls upward and downward on the segment adjacent to it a slightly larger value of $x$ and, as a result does work upon the string segment to which wave is travelling.
For example, the portion of string at point $A$ is going upward, and will pull the portion at point $B$ upward as well. In fact, at any point along the string, each segment of the string is pulling on the segment just adjacent and to its right, causing the wagve to propagate. It is by this process that the energy is sent along the string.
Now we try to calculate how much energy is propagated down the string per second
$T_{y} = t sin θ \approx T tan θ \Rightarrow T_{y} = - T \frac{\partial y}{\partial x}$
(The negative sign appears because as shown in the figure II, the slope is negative) the force will act through a distance
$d y = v_{y} d t = \frac{\partial y}{\partial t} d t$
Therefore work done by force in time $d t$ is
$d W = T_{y} d y = - T (\frac{\partial y}{\partial x}) (\frac{\partial y}{\partial t}) d t \Rightarrow d W = \frac{ω^{2} y_{0}^{2} T}{v} {cos}^{2} [ω (t - \frac{x}{V})] d t$ .....(A)

How much average power is transmitted dawn a string having density $μ = 5 \times 10^{- 4} k g / m$ and $T = 5 N$ by a $200 H z$ vibration of amplitude of $0.20 c m$
A $0.08$ Watt
B $0.16$ Watt
C $0.32$ Watt
D $0.64$ Watt
Question 2 - Select One
If a wave is propagated along the stretched string in the form
ALongitudinal wave
BElectromagnetic wave
CTransverse wave
DAll of the above
Question 3 - Select One
A sinusoidal transverse wave is traveling on a string. Any point on the string
Amoves in the same direction as the wave.
Bmoves in simple harmonic motion with a different frequency than that of the wave.
Cmoves in simple harmonic motion with the same angular frequency as the wave
Dmoves in uniform circular motion with a different angular speed than the wave.