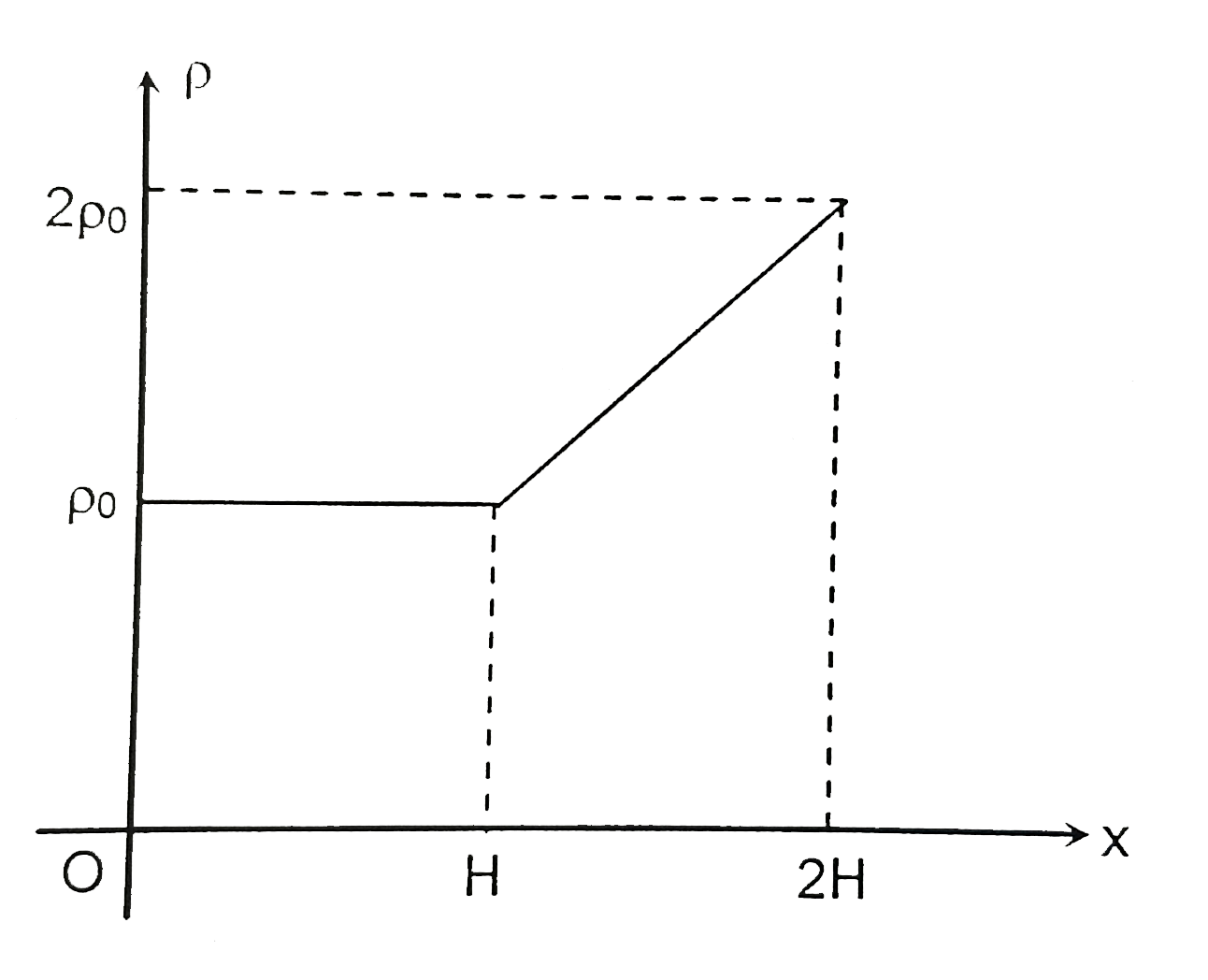
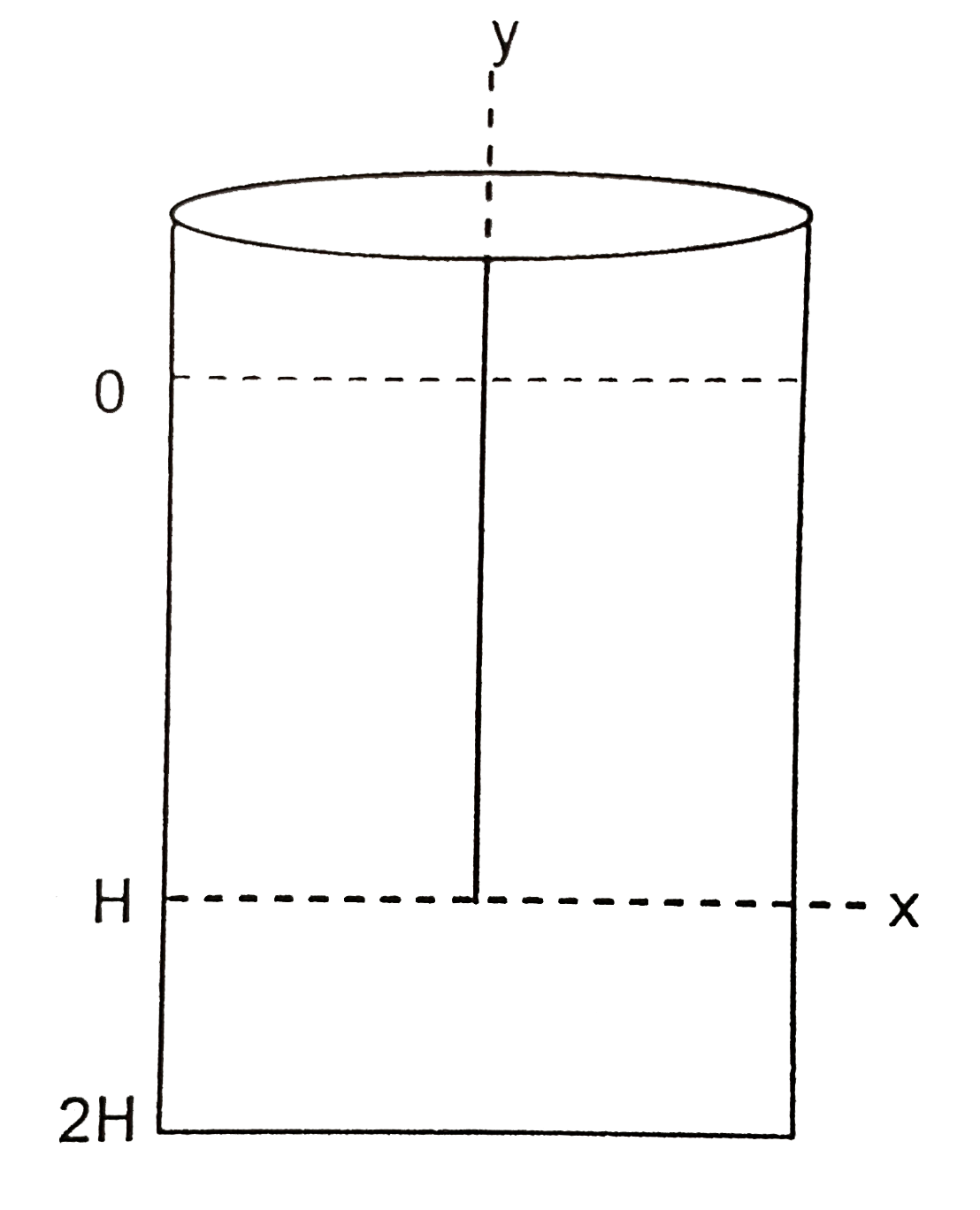
A large cylindrical container with open top contains a liquid upto height and whose density varies as shown in the figure. Atmospheric pressure is 1 atm
Find the pressure at botom of cylindrical container in atm.
(given and )
The correct Answer is:2
We have to calculate the partial pressure, generated due the liquid of variable density
weight of liquid column above the point
Patial pressure at interface due to liquid with variable density
Pressure at bottom
atm
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Water (ρ=103kg/m3) is filled in tube AB as shown in figure. (ω=10rad/s). Tube is open at end A. Atmospheric pressure is p0=105N/m2. Find absolute pressure at endB.
 .
.
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass "100g" as shown in the figure.The radius of the piston is "10cm" .If the atmospheric pressure is P0 then the pressure difference of the liquid just below the piston and the atmospheric pressure is (g=10ms2)
View Solution
Knowledge Check
One bar is equivalent of 105N/m2. The atmosphere pressure is 1.0313×105N/m2. The same in bar is
A1.88 barB1.013 barC2.013 barDnone of theseA cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density ρ1=600kg/m3 and ρ2=1200kg/m3 as shown in the figure.
A small hole having cross sectional area 5cm2 is made in right side vertical wall as shown. Take atmospheric pressure as p0=105N/m2,g=10m/s2. For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm2. Neglect the mass of the vessel.
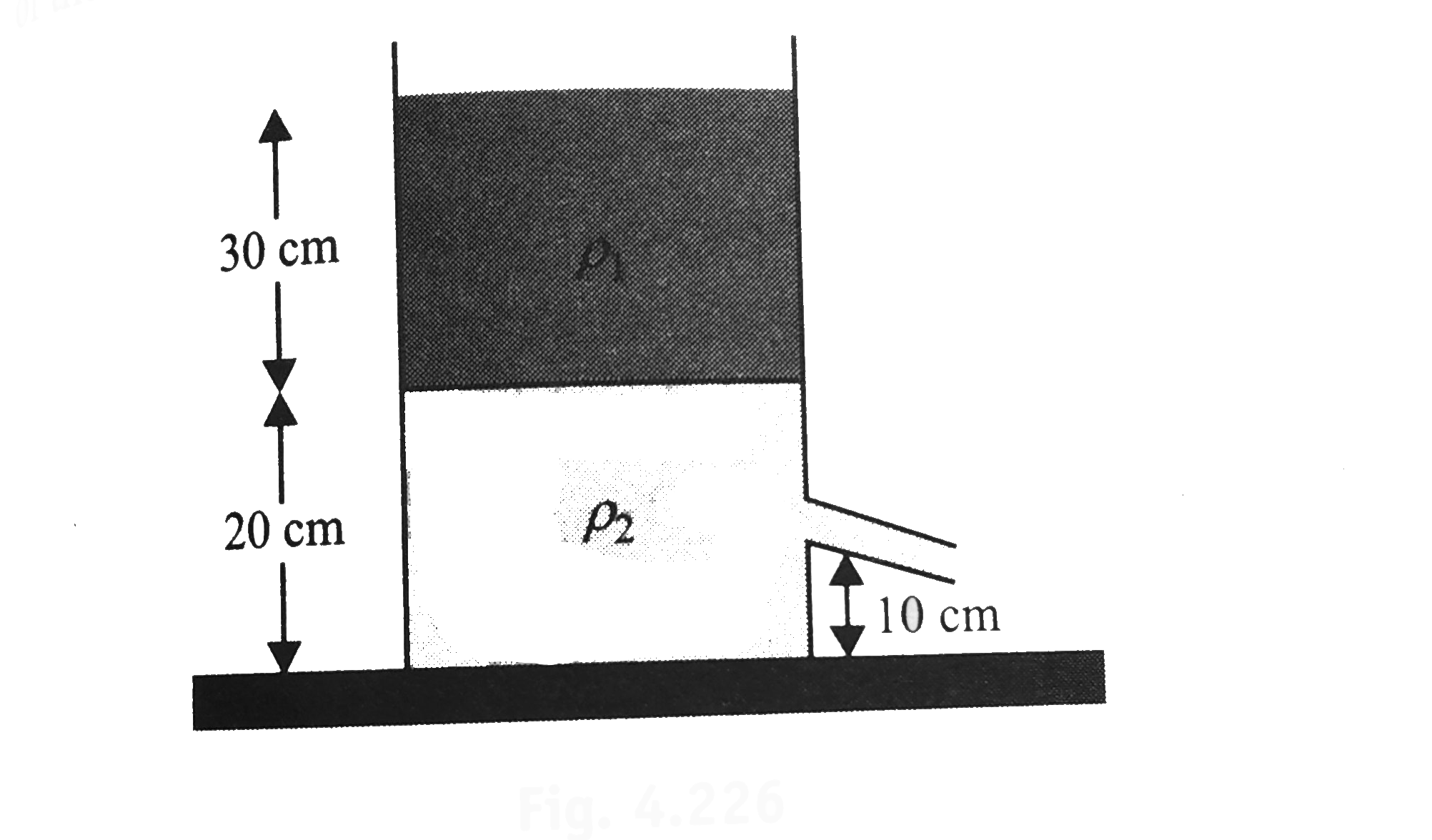 AIf the surface on which the vessel is placed is smooth, then a rightward force of magnitude 3N is to be applied on the vessel to maintain its static equilibrium.BIf the surface on which the vessel is placed is smooth, then no force is needed to maintain its static equilibrium.CIf the surface on which the vessel is placed is rough (μ=0.04), then the minimum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is zero.DIf the surface on which the vessel is placed is rough (=0.04) then the maximum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is 19.8N.
AIf the surface on which the vessel is placed is smooth, then a rightward force of magnitude 3N is to be applied on the vessel to maintain its static equilibrium.BIf the surface on which the vessel is placed is smooth, then no force is needed to maintain its static equilibrium.CIf the surface on which the vessel is placed is rough (μ=0.04), then the minimum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is zero.DIf the surface on which the vessel is placed is rough (=0.04) then the maximum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is 19.8N.A liquid of mass 1 kg is filled in a flask as shown in figure. The force exerted by the flask on the liquid is (g=10m/s2) [Neglect atmospheric pressure]:
 A10 NBgreater than 10NCless than 10NDzero
A10 NBgreater than 10NCless than 10NDzero
Calculate the total pressure at the bottom of a lake of depth 5.1 m (atm pressure =105 P), density of water =103kg/m3,g=10m/s2
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View Solution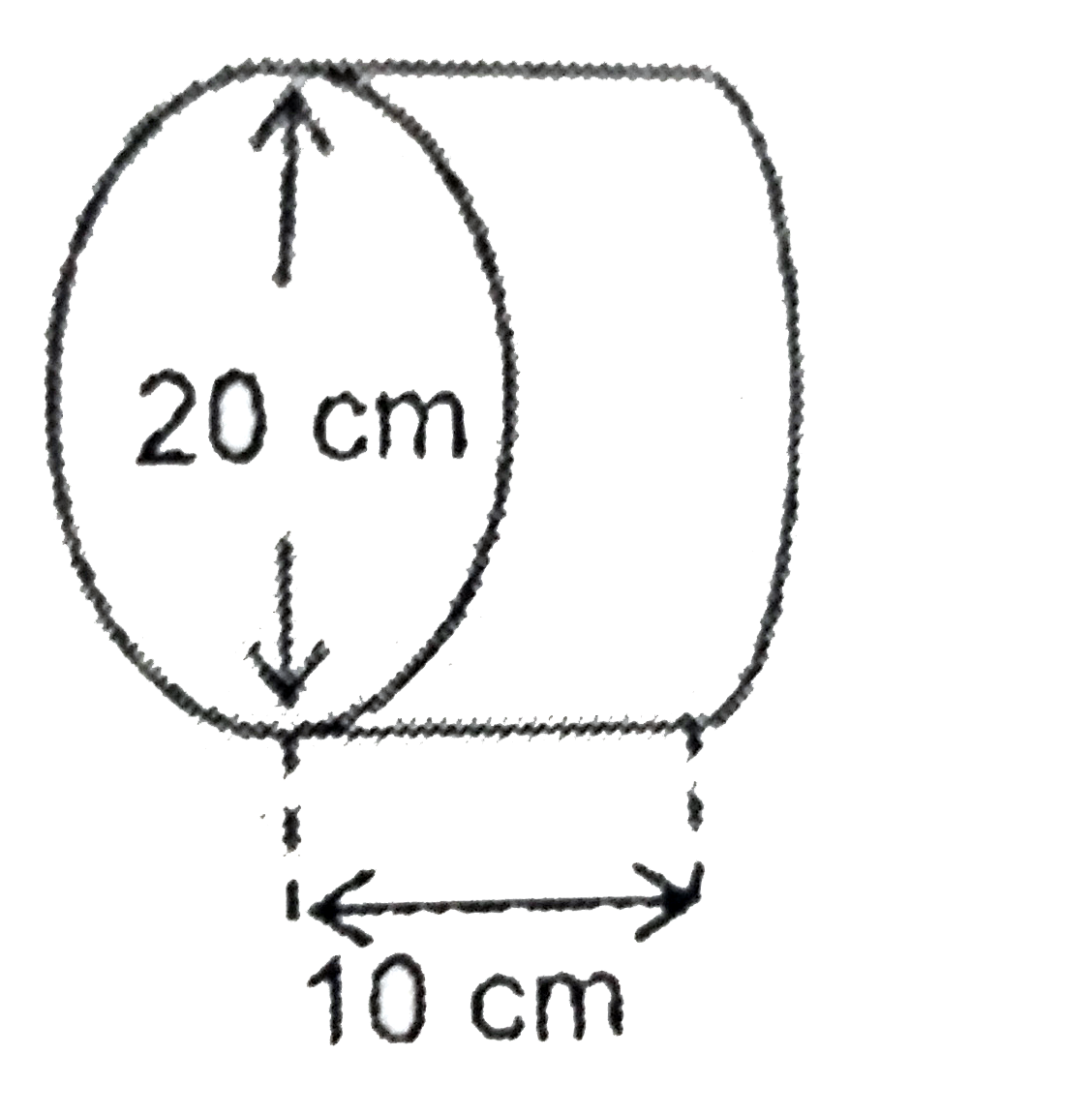
The density of the solid cylindrical bar shown in the figure is5×103 kg m−3 . The weight of the bar is _________ N. (take g=10 m s2
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)

Pressure at point B is
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)
Pressure at point C is
View Solution
