A spherical ball of the radius R is made by joining two hemispherical parts. The two parts have density ρ and 2ρ. When placed in a water tank, the ball floats while remaining completely submered.
(a) If density of water is ρ0, find ρ
(b) Find the time period of small angular oscillations of the ball about its equilibrium position. Neglect viscous forces.
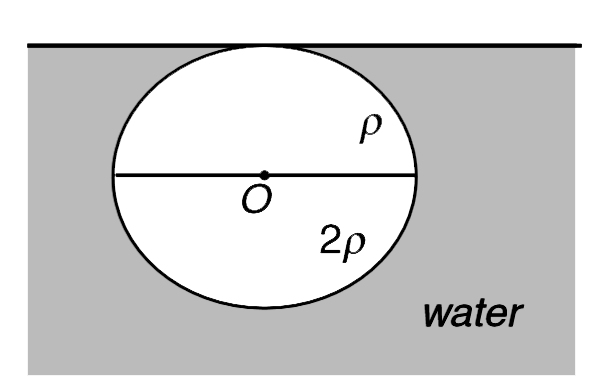
The correct Answer is:(a) ρ=2ρ03 (b) T=2π√12340g
Step by step video, text & image solution for A spherical ball of the radius R is made by joining two hemispherical parts. The two parts have density rho and 2rho. When placed in a water tank, the ball floats while remaining completely submered. (a) If density of water is rho_(0), find rho (b) Find the time period of small angular oscillations of the ball about its equilibrium position. Neglect viscous forces. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
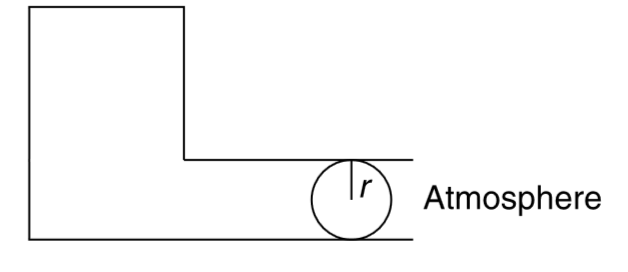
A ball of radius r fits tightly inside a tube attached to a container. There is no friction between the tube wall and the ball. Volume of air inside the container is V0 when the ball is in equilibrium. Density of the material of the ball is d and atmospheric pressure is P0. If the ball is displaced a little from its equilibrium position and released, find time period of its oscillation. Assume that temperature in the container remains constant and that air is an ideal gas.
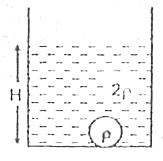
View SolutionA small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
View Solution
Knowledge Check

A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
Find the force exerted by the liquid with density 2ρ on the ballAπR2ρg(H+2R3)B23πR2ρgC43πR2ρgD2πR2ρg(H+2R3)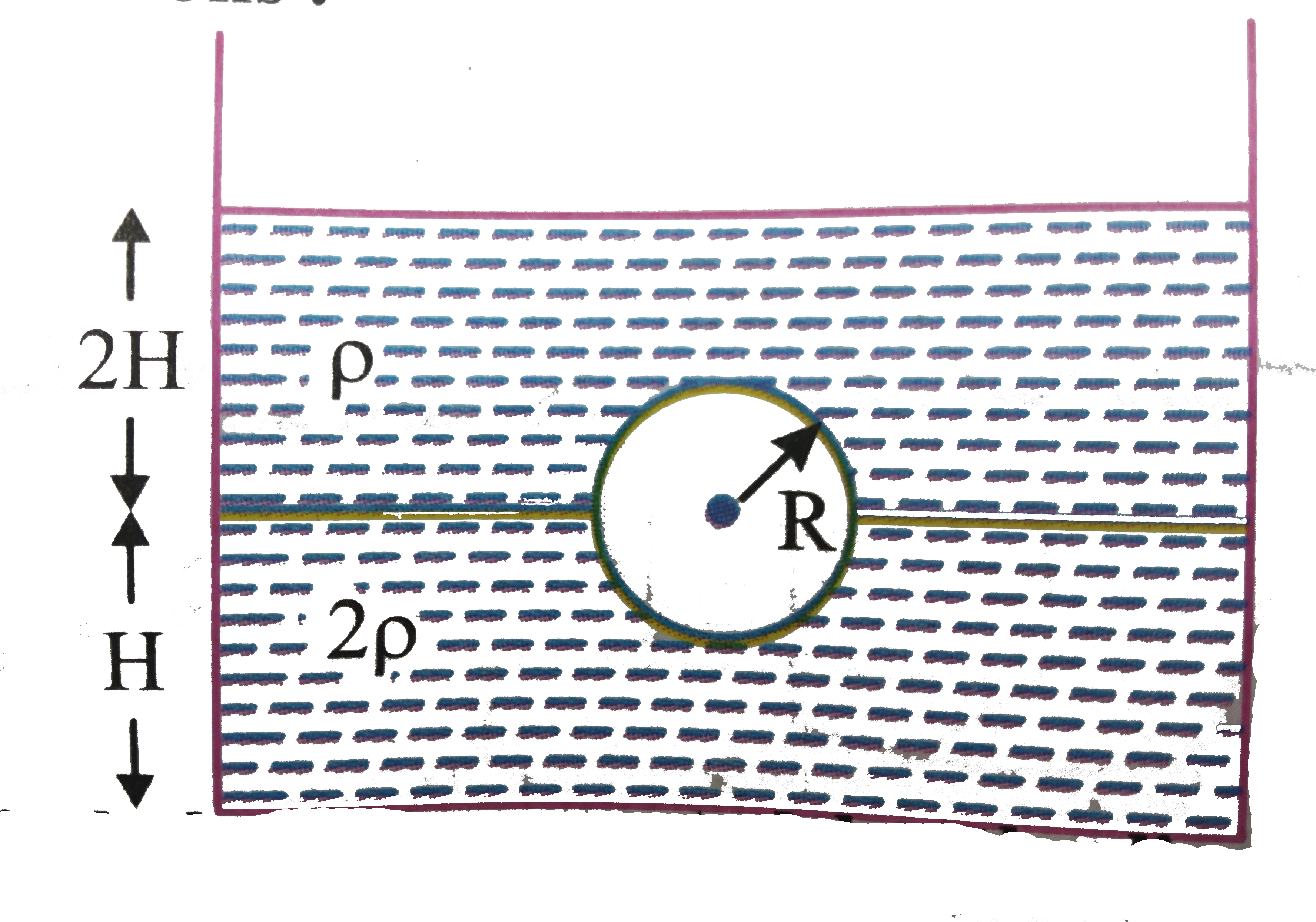
A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
If a hole is drilled at the bottom of the vessel then volume of the ball immersed inliquid with density ρ willAremain sameBdecreaseCincreaseDdecrease first then increaseA sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ρ is the density of water]-
A0.25 ρrgB0.5 ρ rgC43πr3ρgD512πr4ρg
A rubber ball of mass m and radius r is submerged in water to a depth h and released. What height will the ball jump up to above the surface of the water? Neglect ther resistance of water and air. Take water density ρ.
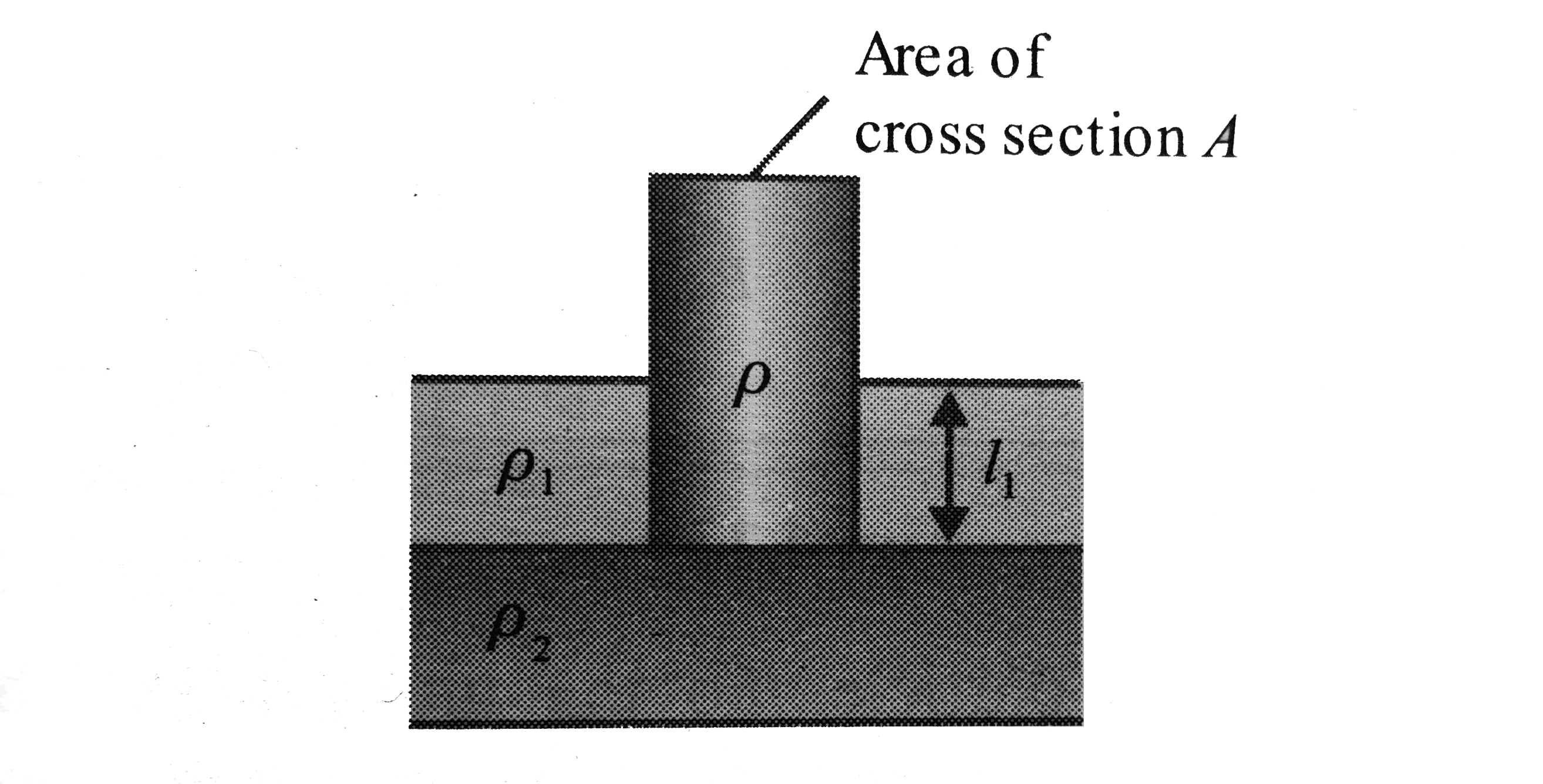
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View SolutionA ball of relative density 0.8 falls into water from a height of 2 m. find the depth to which the ball will sink (neglect viscous forces)
View SolutionA small ball of density 4ρ0 is released from rest just below the surface of a liquid. The density of liquid increases with depth as ρ=ρ0(1+ay) where a=2m−1 is a constant. Find the time period of its oscillation. (Neglect the viscosity effects).
View Solution
