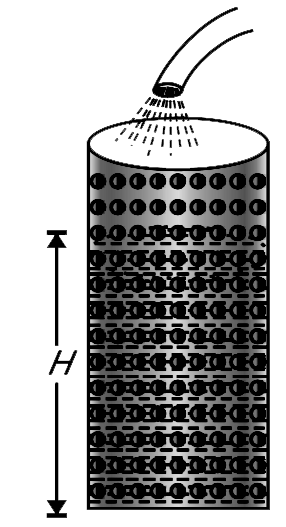
A cylinderical container having radius r has perforated wall. There are large number of uniformly spread small holes on the vertical wall occupying a fraction of the entire area of the wall. To maintain the water level at height H in the contaienr water is being fed to it at a cosntant rate . find q.
The correct Answer is:
Step by step video, text & image solution for A cylinderical container having radius r has perforated wall. There are large number of uniformly spread small holes on the vertical wall occupying a fraction eta=0.02 of the entire area of the wall. To maintain the water level at height H in the contaienr water is being fed to it at a cosntant rate Q(m^(3)s^(-1)). find q. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Water flows out of a small hole in the wall of a large tank near its bottom. What is the speed of efflux of water when height of water level in the tank is 5.0 m ?
View Solution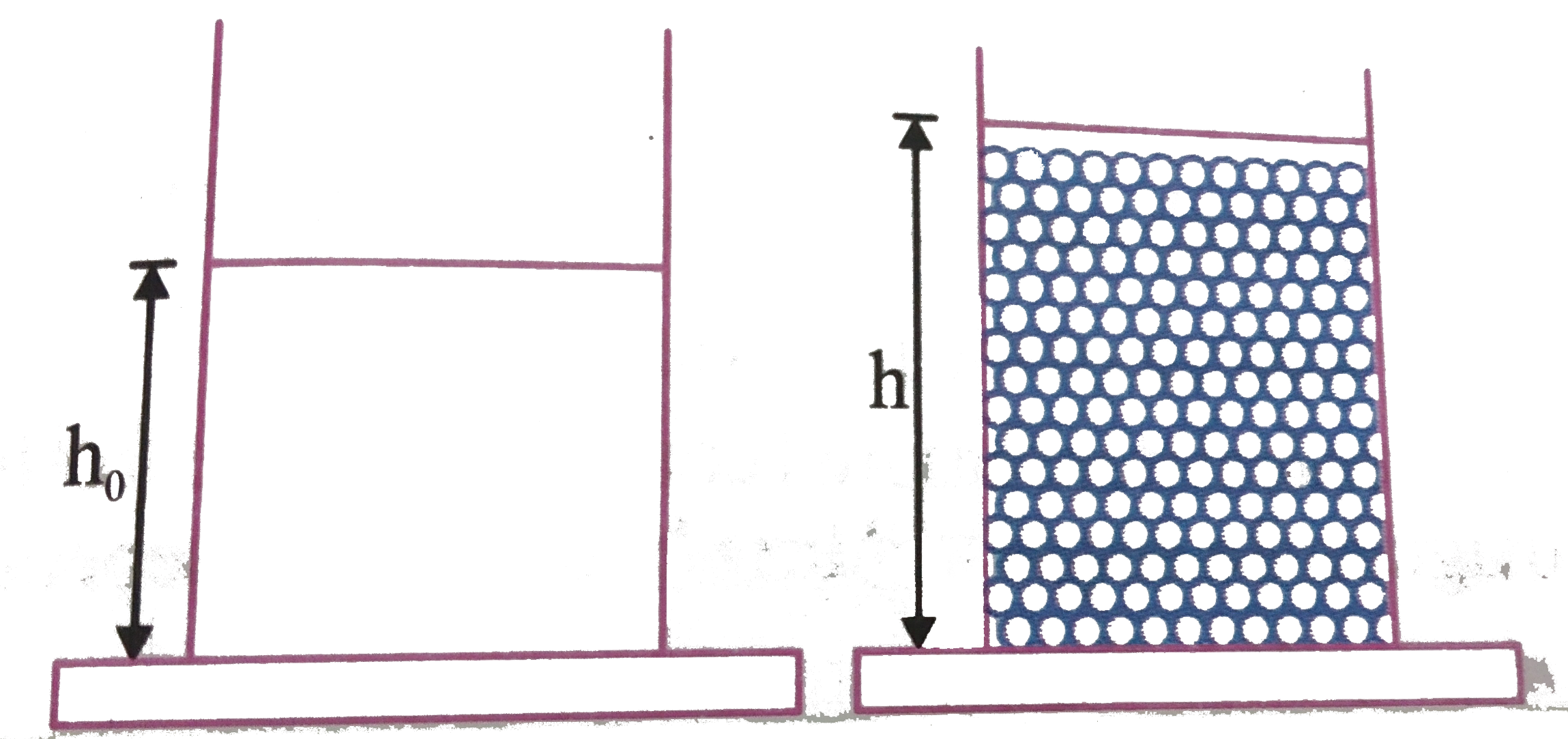
In a cylindrical container water is filled up to a height of h0=1.0m. Now a large number of small iron balls are gently dropped one by one into the container till the upper layer of the balls touches the water surface. if average density of the contents is ρ=4070kg/m3, density of iron is ρi=7140kg/m3 and density of iron is ρ0=1000kg/m3 find the height h of the water level (in S.I. units) in the container with the iron balls.
View Solution
Knowledge Check
A container has a small hole at its bottom. Area of cross-section of the hole is A1 and that of the container is A2. Liquid is poured in the container at a constant rate Qm3s−1. The maximum level of liquid in the container will be
AQ22gA1A2BQ22gA21CQ2gA1A2DQ22gA2^(2)Two identical tall jars are filled with water to the brim. The first jar has a small hole on the side wall at a depth h/3 and the second jar has a small holw on the side wall at a depth of 2h/3, where h is the height of the jar. The water issuing out from the first jar falls at a distance R1 from the base and the water issuing out from the second jar falls at a distance R2 From the base. The correct relation between R1 and R2 is
AR1>R2BR1<R2CR2=2×R1DR1=R2Oil is filled in a cylindrical container up to height 4m. A small hole of area 'p' is punched in the wall of the container at a height 1.52m from the bottom. The cross sectional area of the container is Q. Ifpq=0.1 then v is (where vis the velocity of oil coming out of the hole)
A5√2B6√3C8√2D7√5
A cylindrical container has insulating wall and an insulating piston which can freely move up and down without any friction. It contains a mixture of ideal gases. Originally the gas is at atmospheric pressure P0 and temperature (T0). A tap positioned above the container is opened and it supplies water at a constant rate of dmdt=0.25kg/s. The water collects above the piston in the container and the gas compresses. The tap is kept open till the temperature of the gas is doubled. During the process the T vs 1V graph for the gas was recorded and found to be a parabola with its vertex at origin as shown in the graph. Area of piston A=1.515×10−3m2 and atmospheric pressure =105N/m2
(a) Find the ratio of Vrms and speed of sound in the gaseous mixture.
(b) For how much time the tap was kept open?
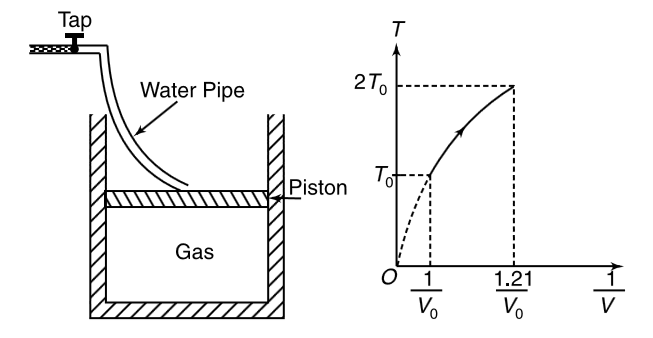
View SolutionA cylindrical container has cross sectional area of 0.20m2 and is open at the top. At the bottom, it has a small hole (A) kept closed by a cork. There is an air balloon tied to the bottom surface of the container. Volume of balloon is 2.2 litre. Now water is filled in the container and the balloon gets fully submerged. Volume of the balloon reduces to 2.0 litre. The cork is taken out to open the hole and at the same moment the whole container is dropped from a large height so as to fall under gravity. Assume that the container remains vertical. find the change in level of water inside the falling container 2 second after it starts falling.
View SolutionA canon can fire shells at speed u. Inclination of its barrel to the horizontal can be changed in steps of Δθ=1∘ ranging from θ1=15∘ to θ2=85∘. Let Rn be the horizontal range for projection angle θ=n∘.
ΔRn=|Rn−Rn+1|
For what value of n the value of ΔRn is maximum? Neglect air resistance.
(ii) A small water sprinkler is in the shape of a hemisphere with large number of uniformly spread holes on its surface. It is placed on ground and water comes out of each hole with speed u. Assume that we mentally divide the ground into many small identical patches – each having area ΔS. What is the distance of a patch from the sprinkler which receives maximum amount of water ?
View SolutionTwo capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
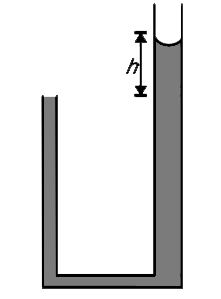
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .
View SolutionThe diagram shows a tall cylindrical container kept on a horizontal surface. From a tap, water come with constant rate qm3/s. Initially the container was empty. An orifice of area of cross section A is made at some height h in the side wall of the container. If the horizontal range of the water jet in steady is found to be 2h, then the relation between h and q is

View Solution