A water tank has a small hole in its wall and a tapering nozzle has been fitted into the hole (figure). The diameter of the nozzle at the exit is d0=1cm. The height of water in the tank above the central line of the nozzle is h=2.0m.
Calculate the dischargerate in m3s−1 through the nozzle. Another nozzle which is diverging outwards is fitted smoothly to the first nozzle. The pressure at the neck of the two nozzle (where diameter is d0) drops ot 2.5m of water. Calculate the exit diameter (d) of the nozzle.
Atmosphere pressure =10m of water and g=10ms−2
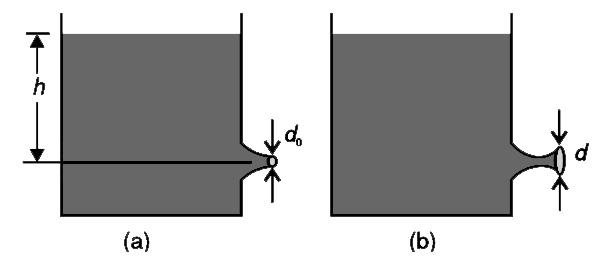
The correct Answer is:(a) 4.96×10−4m3s−1
(b) 1.48cm
Step by step video, text & image solution for A water tank has a small hole in its wall and a tapering nozzle has been fitted into the hole (figure). The diameter of the nozzle at the exit is d_(0)=1cm. The height of water in the tank above the central line of the nozzle is h=2.0m. Calculate the dischargerate in m^(3)s^(-1) through the nozzle. Another nozzle which is diverging outwards is fitted smoothly to the first nozzle. The pressure at the neck of the two nozzle (where diameter is d_(0)) drops ot 2.5m of water. Calculate the exit diameter (d) of the nozzle. Atmosphere pressure =10m of water and g=10ms^(-2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Water flows out of a small hole in the wall of a large tank near its bottom. What is the speed of efflux of water when height of water level in the tank is 5.0 m ?
View SolutionWater flow througyh a horizontal pipe whose internal diameter is 2.0cm at a speed of 1.0ms−1 What should be the diameter of the nozzle, If the water is to emerge at a speed of 4.0ms−1?
View Solution
Knowledge Check
A water tank has a hole in its wall at a distance of 40 m below the free surface of water. Compute the velocity of flow of water from the hole. If the radius of the hole is 1 mm. find the rate of flow of water
A26m/s,8.8×10−5m3/sB28m/s,8.8×10−5m3/sC28m/s,6.8×10−5m3/5D26m/s,9.8×10−5m3/sA tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)A tank full of water has a small hole at its bottom. Let t1 be the time taken to empty the first half of the tank and t2 be the time needed to empty the rest half of the tank, then
At1=t2Bt1>t2Ct1<t2Dt1=0.523t2
A water tank has a circular hole at its base. A solid cone is used to plug the hole. Exactly half the height of the cone protrudes out of the hole. Water is filled in the tank to a height equal to height of the cone. Caluclate the buoyancy force on the conc. Density of water is ρ and volume of cone is V.
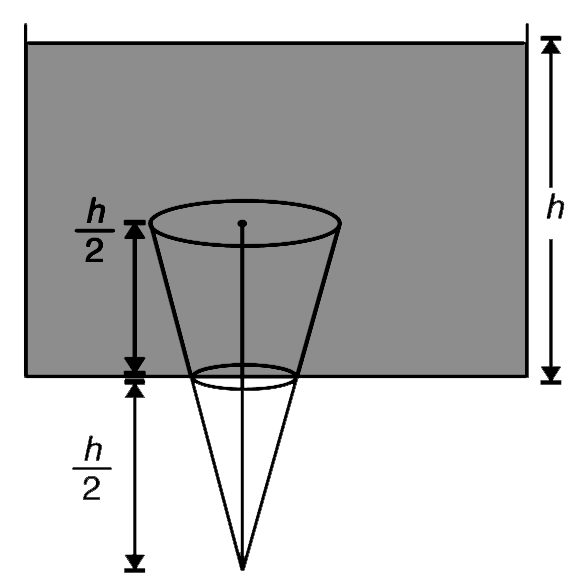
View SolutionA cylindrical tank has a hole of 1 cm in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm/sec . then the maximum height up to which water can rise in the tank is
View SolutionA cylinderal tank has a hole of 1.6cm2 in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 80cm3/s, then the maximum height up to which water can water can rise in the tank is
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionA vessel has a small hole at its bottom. If water can be poured into it upto a height of 7 cm without leakage (g=10ms−2) the radius of the hole is (surface tension of water is 0.7Nm−1)
View Solution