Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
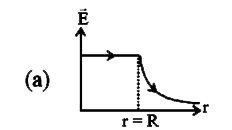
To determine the variation of the electric field (E) with distance (r) from the center of a charged spherical conductor of radius R, we need to analyze two cases: when the sphere is a hollow conductor and when it is a solid conductor.
1. When r < R (Inside the hollow sphere):
- According to Gauss's law, the electric field inside a hollow conductor is zero because there is no charge enclosed within the Gaussian surface.
- Thus, E=0.
2. When r = R (On the surface of the hollow sphere):
- The electric field at the surface can be calculated using the formula:
E=kQR2
- Here, k is Coulomb's constant, and Q is the total charge on the sphere.
3. When r > R (Outside the hollow sphere):
- For points outside the hollow sphere, we can treat the entire charge as if it were concentrated at the center:
E=kQr2
- This shows that the electric field decreases with the square of the distance from the center.
Graph for the Hollow Sphere:
- The graph will show that for r<R, E=0. At r=R, E jumps to kQR2, and for r>R, E decreases as 1r2.
Case 2: Solid Spherical Conductor
1. When r < R (Inside the solid sphere):
- For a solid sphere, the electric field inside is calculated using the formula:
E=kQrR3
- This indicates that the electric field increases linearly with distance r from the center.
2. When r = R (On the surface of the solid sphere):
- The electric field at the surface is the same as for the hollow sphere:
E=kQR2
3. When r > R (Outside the solid sphere):
- Similar to the hollow sphere, we treat the charge as concentrated at the center:
E=kQr2
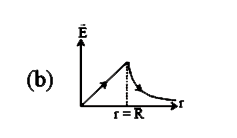
Graph for the Solid Sphere:
- The graph will show that for r<R, E increases linearly from 0 to kQR2 at r=R. For r>R, the electric field decreases as 1r2.
Conclusion:
- For a hollow spherical conductor, the graph starts at zero, jumps to a constant value at the surface, and then decreases with 1r2.
- For a solid spherical conductor, the graph increases linearly until the surface and then decreases with 1r2.
Final Answer:
- The correct graphs representing the variation of electric field with distance r from the center of a charged spherical conductor are:
- Option B for the solid sphere.
- Option C for the hollow sphere.
- According to Gauss's law, the electric field inside a hollow conductor is zero because there is no charge enclosed within the Gaussian surface.
- Thus, E=0.
- The electric field at the surface can be calculated using the formula:
E=kQR2
- Here, k is Coulomb's constant, and Q is the total charge on the sphere.
- For points outside the hollow sphere, we can treat the entire charge as if it were concentrated at the center:
E=kQr2
- This shows that the electric field decreases with the square of the distance from the center.
- The graph will show that for r<R, E=0. At r=R, E jumps to kQR2, and for r>R, E decreases as 1r2.
- For a solid sphere, the electric field inside is calculated using the formula:
E=kQrR3
- This indicates that the electric field increases linearly with distance r from the center.
- The electric field at the surface is the same as for the hollow sphere:
E=kQR2
- Similar to the hollow sphere, we treat the charge as concentrated at the center:
E=kQr2
- The graph will show that for r<R, E increases linearly from 0 to kQR2 at r=R. For r>R, the electric field decreases as 1r2.
- For a hollow spherical conductor, the graph starts at zero, jumps to a constant value at the surface, and then decreases with 1r2.
- For a solid spherical conductor, the graph increases linearly until the surface and then decreases with 1r2.
- The correct graphs representing the variation of electric field with distance r from the center of a charged spherical conductor are:
- Option B for the solid sphere.
- Option C for the hollow sphere.
Topper's Solved these Questions
Similar Questions
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0≤r≤0 .
View SolutionA hollow charged sphere of radius R has a constant surface charge density o. Of the following graphs the one, which shows the variation of the electric field strength E with distance X from the centre of the sphere is (A) E I=R x (B) E 1
View Solution
Knowledge Check
An isolated non-conducting solid sphere of radius R is given an electric charge. The charge is uniformly distributed in the volume of sphere. The graph which shows the correct variation of magnitude of electric field with distance from the centre of the sphere is
A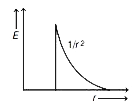 B
B C
C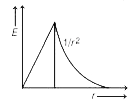 D
D
Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A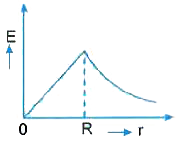 B
B CD
CD
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B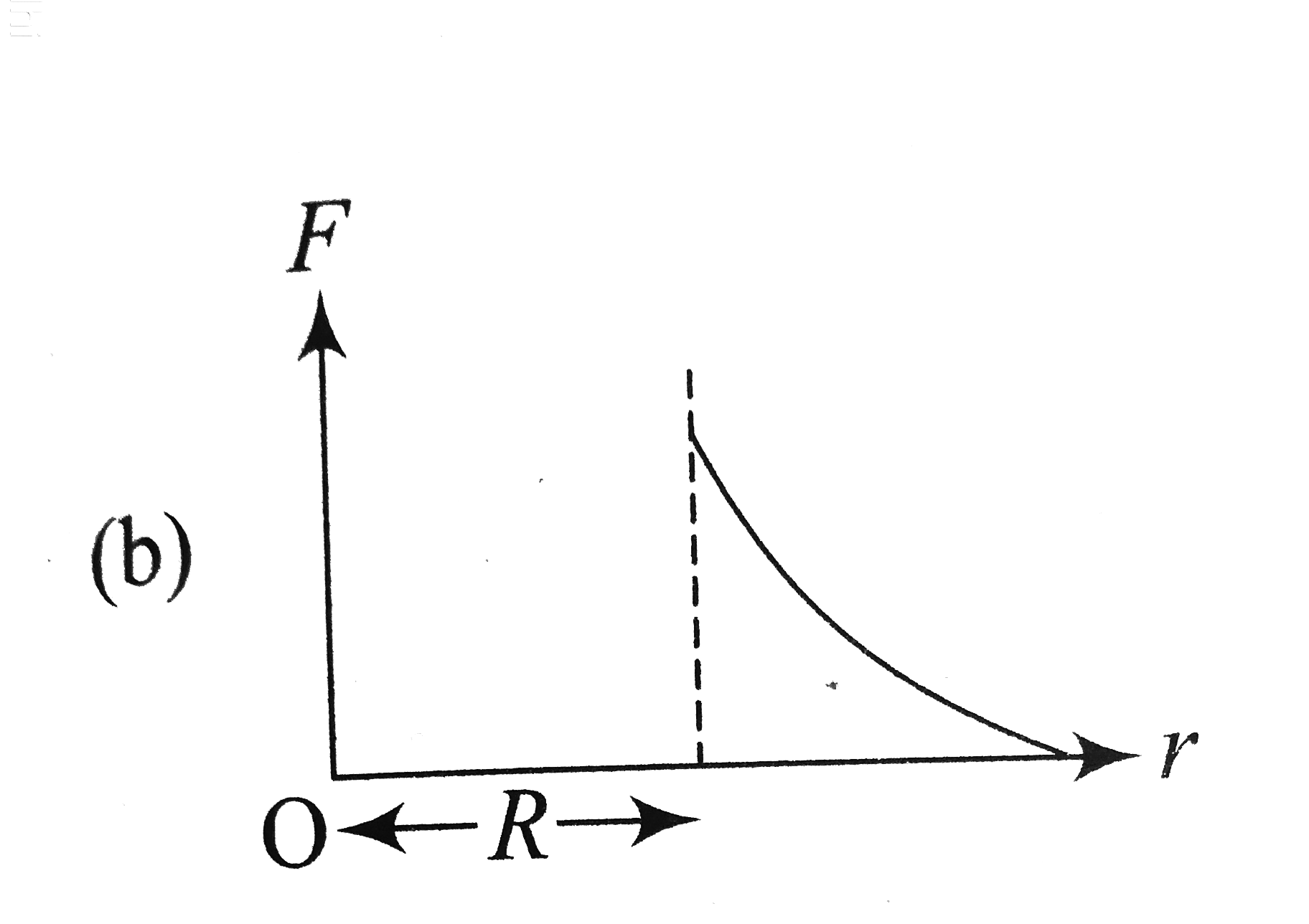 C
C D
D
Which one of t he following plots represents the variation of gravitational field of a particle with distance r due to thin spherical shell of radius R ?
View SolutionWhich one of the following graphs represents correctly represent the variation of the gravitational field (E) with the distance (r) from the centre of a spherical shell of mass M radius R ?
View SolutionConsider a uniform spherical volume charge distribution of radius R. Which of the following graphs correctly represents the magnitude of the electric field E as a distance r from the center of the sphere ?
View SolutionA metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?
View SolutionWhich graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?
View Solution
