Draw a graph of electric field E(r) with distance r from the centre of the shell for .
To draw the graph of the electric field E(r) with distance r from the center of a charged spherical shell for 0≤r≤R (where R is the radius of the shell), we can follow these steps:
Step 1: Understanding the Electric Field Inside a Charged Shell
For a uniformly charged spherical shell, the electric field inside the shell (for r<R) is zero. This is a consequence of Gauss's law, which states that the electric field inside a closed conductor is zero when in electrostatic equilibrium.
Step 2: Electric Field at the Surface of the Shell
At the surface of the shell (where r=R), we can calculate the electric field using Gauss's law. The electric field just outside the surface of the shell is given by:
E=14πϵ0QR2
where Q is the total charge on the shell.
Step 3: Electric Field for r<R
Since we established that the electric field inside the shell is zero, we can denote this on our graph. For all values of r from 0 to R, the electric field E(r) remains zero.
Step 4: Graphing the Electric Field
Now we can plot the graph:
- On the x-axis, we will represent the distance r from the center of the shell, ranging from 0 to R.
- On the y-axis, we will represent the electric field E(r).
1. For 0<r<R: E(r)=0
2. At r=R: E(r) jumps to a positive value 14πϵ0QR2.
Step 5: Indicating the Values on the Graph
- Draw a horizontal line along the x-axis from r=0 to r=R at E=0.
- At r=R, draw a point indicating the value of the electric field E=14πϵ0QR2.
Final Graph
The graph will look like this:
- A horizontal line at E=0 from r=0 to r=R.
- A point at (R,14πϵ0QR2) indicating the electric field at the surface of the shell.
For a uniformly charged spherical shell, the electric field inside the shell (for r<R) is zero. This is a consequence of Gauss's law, which states that the electric field inside a closed conductor is zero when in electrostatic equilibrium.
At the surface of the shell (where r=R), we can calculate the electric field using Gauss's law. The electric field just outside the surface of the shell is given by:
E=14πϵ0QR2
where Q is the total charge on the shell.
Since we established that the electric field inside the shell is zero, we can denote this on our graph. For all values of r from 0 to R, the electric field E(r) remains zero.
Now we can plot the graph:
- On the x-axis, we will represent the distance r from the center of the shell, ranging from 0 to R.
- On the y-axis, we will represent the electric field E(r).
2. At r=R: E(r) jumps to a positive value 14πϵ0QR2.
- Draw a horizontal line along the x-axis from r=0 to r=R at E=0.
- At r=R, draw a point indicating the value of the electric field E=14πϵ0QR2.
The graph will look like this:
- A horizontal line at E=0 from r=0 to r=R.
- A point at (R,14πϵ0QR2) indicating the electric field at the surface of the shell.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Revision Exercises (Long Answer )
Explore 15 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Revision Exercises (Numerical Problems )
Explore 7 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Revision Exercises (Fill in the Blanks )
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View Solution
Knowledge Check
A conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
A B
B C
C D
D
A metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?
A B
B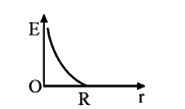 C
C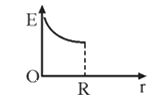 D
D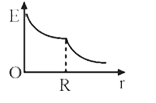
Two concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure

If we daw a graph between electric field E and distance r from the centre, it will be likeA B
B C
C D
D
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
The graph of the radial component of E as function of r will be
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radus R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionWhich one of the following graphs represents correctly represent the variation of the gravitational field (E) with the distance (r) from the centre of a spherical shell of mass M radius R ?
View Solution