Three point charges in the order are placed equally spaced along a straight line. and are equal in magnitude but opposite in sign. If the net force on is zero. The value of is
To solve the problem, we need to analyze the forces acting on the charge Q3 due to the other charges Q1 and Q2. Given that Q2 and Q3 are equal in magnitude but opposite in sign, we can denote their values as follows:
- Let Q2=+q
- Let Q3=−q
- Let Q1=Q (unknown charge we need to find)
Step 1: Understanding the Configuration
The charges are arranged in a straight line with equal spacing. We can denote the positions of the charges as follows:
- Q1 is at position x1
- Q2 is at position x2
- Q3 is at position x3
Assuming the distance between each charge is d:
- x1=0
- x2=d
- x3=2d
Step 2: Calculating Forces on Q3
The net force on Q3 is zero, which means the forces acting on it due to Q1 and Q2 must balance each other.
1. Force due to Q2 on Q3:
The force F23 between Q2 and Q3 is given by Coulomb's law:
F23=k|Q2⋅Q3|d2=k|q⋅(−q)|d2=kq2d2
This force is attractive since Q2 is positive and Q3 is negative, acting towards Q2.
2. Force due to Q1 on Q3:
The force F13 between Q1 and Q3 is also given by Coulomb's law:
F13=k|Q1⋅Q3|(2d)2=k|Q⋅(−q)|4d2=kQq4d2
This force is repulsive if Q1 is positive (acting away from Q1) and attractive if Q1 is negative (acting towards Q1).
Step 3: Setting the Forces Equal
Since the net force on Q3 is zero, we can set the magnitudes of the forces equal to each other:
F23=F13
Substituting the expressions we derived:
kq2d2=kQq4d2
Step 4: Simplifying the Equation
We can cancel k and d2 from both sides (assuming k and d are not zero):
q2=Qq4
Step 5: Solving for Q
Now, we can solve for Q:
4q2=Qq
Dividing both sides by q (assuming q≠0):
Q=4q
Conclusion
Thus, the value of Q1 is:
Q1=4q
- Let Q3=−q
- Let Q1=Q (unknown charge we need to find)
The charges are arranged in a straight line with equal spacing. We can denote the positions of the charges as follows:
- Q1 is at position x1
- Q2 is at position x2
- Q3 is at position x3
- x1=0
- x2=d
- x3=2d
The net force on Q3 is zero, which means the forces acting on it due to Q1 and Q2 must balance each other.
The force F23 between Q2 and Q3 is given by Coulomb's law:
F23=k|Q2⋅Q3|d2=k|q⋅(−q)|d2=kq2d2
This force is attractive since Q2 is positive and Q3 is negative, acting towards Q2.
The force F13 between Q1 and Q3 is also given by Coulomb's law:
F13=k|Q1⋅Q3|(2d)2=k|Q⋅(−q)|4d2=kQq4d2
This force is repulsive if Q1 is positive (acting away from Q1) and attractive if Q1 is negative (acting towards Q1).
Since the net force on Q3 is zero, we can set the magnitudes of the forces equal to each other:
F23=F13
Substituting the expressions we derived:
kq2d2=kQq4d2
We can cancel k and d2 from both sides (assuming k and d are not zero):
q2=Qq4
Now, we can solve for Q:
4q2=Qq
Dividing both sides by q (assuming q≠0):
Q=4q
Thus, the value of Q1 is:
Q1=4q
Topper's Solved these Questions
Similar Questions
Calculate Q1,Q2andQ3,

View SolutionA charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
View Solution
Knowledge Check
The value of charge q1,q2andq3 as shown in the figure are
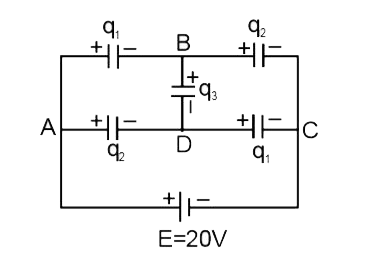 Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μCThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
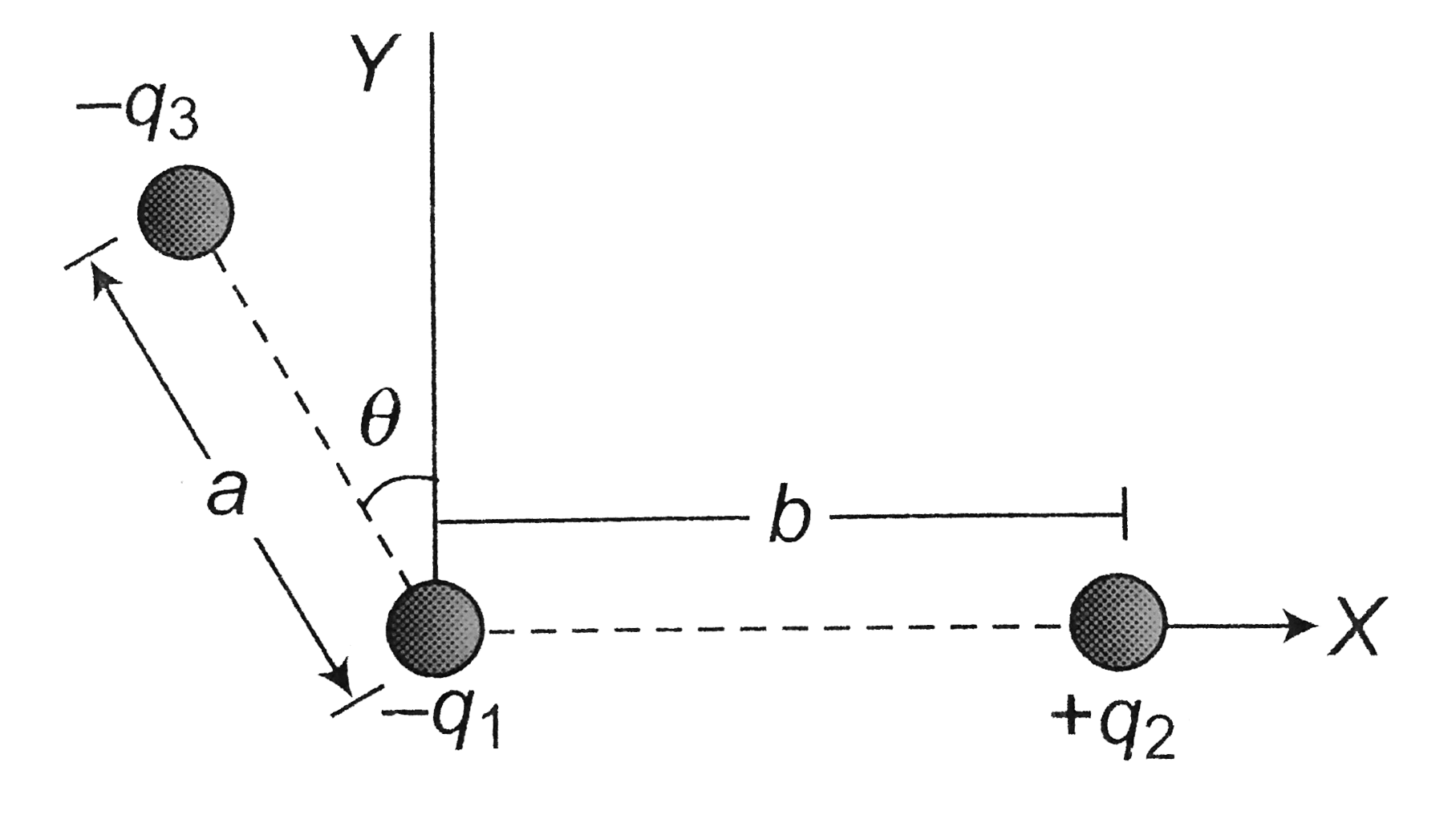 Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2cosθ
Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2cosθThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
 Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2sinθ
Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2sinθ
Three charges +Q, q, +Q are placed respectively, at distance, 0, d//2 and d from the origin, on the x-axis. If the net force experienced by +Q placed at x=0, is zero, then value of q is :
View SolutionThree charged paricles are placed on a straight line as shown in fig. q1 and q2 are fixed but q3 can be moved. Under the action of the forces from q1,q2 and q3 is in equilbrium. What is the relation between q1 and q2.

View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .
.
View SolutionThreee charges +Q1,+Q2 and q are placed on a straight line such that q is somewhere in between +Q1and Q2. If this system of charges is in equlibirium what should be the magnitude and sign of charge q?
View SolutionThree charge q,Q and −4q are placed in a straight line , line of length Lat points distant 0,L/2 and L respectively from one end. In order to make the net force on q zero, the charge Q must be equal to
View Solution
