A metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?

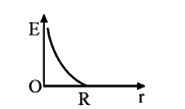
The correct Answer is:C
To solve the problem of determining the variation of electric field E with distance r from the center of a metallic spherical shell with a point charge at its center, we can follow these steps:
Step 1: Understand the Setup
We have a metallic spherical shell of radius R with a total charge of −Q on its surface. A point charge +Q is placed at the center of the shell.
Step 2: Analyze the Electric Field Inside the Shell
According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero. However, since we have a point charge +Q at the center, we need to consider the electric field due to this charge.
- For a point charge, the electric field E at a distance r from the charge is given by:
E=kQr2
where k is Coulomb’s constant.
- Since we are inside the shell (i.e., r<R), the electric field due to the point charge +Q will be:
E=kQr2for r<R
Step 3: Analyze the Electric Field on the Surface of the Shell
At the surface of the shell (i.e., r=R), we can calculate the electric field using Gauss's law. The total charge enclosed by a Gaussian surface just outside the shell is +Q−Q=0 (the point charge and the negative charge on the shell).
- Therefore, the electric field at the surface of the shell is:
E=0for r=R
Step 4: Analyze the Electric Field Outside the Shell
For points outside the shell (i.e., r>R), the total charge enclosed by a Gaussian surface is zero (the positive charge +Q and the negative charge −Q cancel each other out).
- Hence, the electric field outside the shell is:
E=0for r>R
Step 5: Summarize the Electric Field Variation
- For r<R: E=kQr2 (decreases as r increases)
- For r=R: E=0
- For r>R: E=0
Step 6: Graphical Representation
The graph representing this variation will show:
- A curve that starts from a positive value when r is small, decreases as r approaches R, and then becomes zero at r=R and remains zero for r>R.
Conclusion
The correct graph will show the electric field decreasing from a positive value to zero as r approaches R and remaining zero for r>R.
---
We have a metallic spherical shell of radius R with a total charge of −Q on its surface. A point charge +Q is placed at the center of the shell.
According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero. However, since we have a point charge +Q at the center, we need to consider the electric field due to this charge.
E=kQr2
where k is Coulomb’s constant.
E=kQr2for r<R
At the surface of the shell (i.e., r=R), we can calculate the electric field using Gauss's law. The total charge enclosed by a Gaussian surface just outside the shell is +Q−Q=0 (the point charge and the negative charge on the shell).
E=0for r=R
For points outside the shell (i.e., r>R), the total charge enclosed by a Gaussian surface is zero (the positive charge +Q and the negative charge −Q cancel each other out).
E=0for r>R
- For r<R: E=kQr2 (decreases as r increases)
- For r=R: E=0
- For r>R: E=0
The graph representing this variation will show:
- A curve that starts from a positive value when r is small, decreases as r approaches R, and then becomes zero at r=R and remains zero for r>R.
The correct graph will show the electric field decreasing from a positive value to zero as r approaches R and remaining zero for r>R.
Similar Questions
Knowledge Check
- Question 1 - Select One
Which one of the following graphs represents correctly represent the variation of the gravitational field (E) with the distance (r) from the centre of a spherical shell of mass M radius R ?
A B
B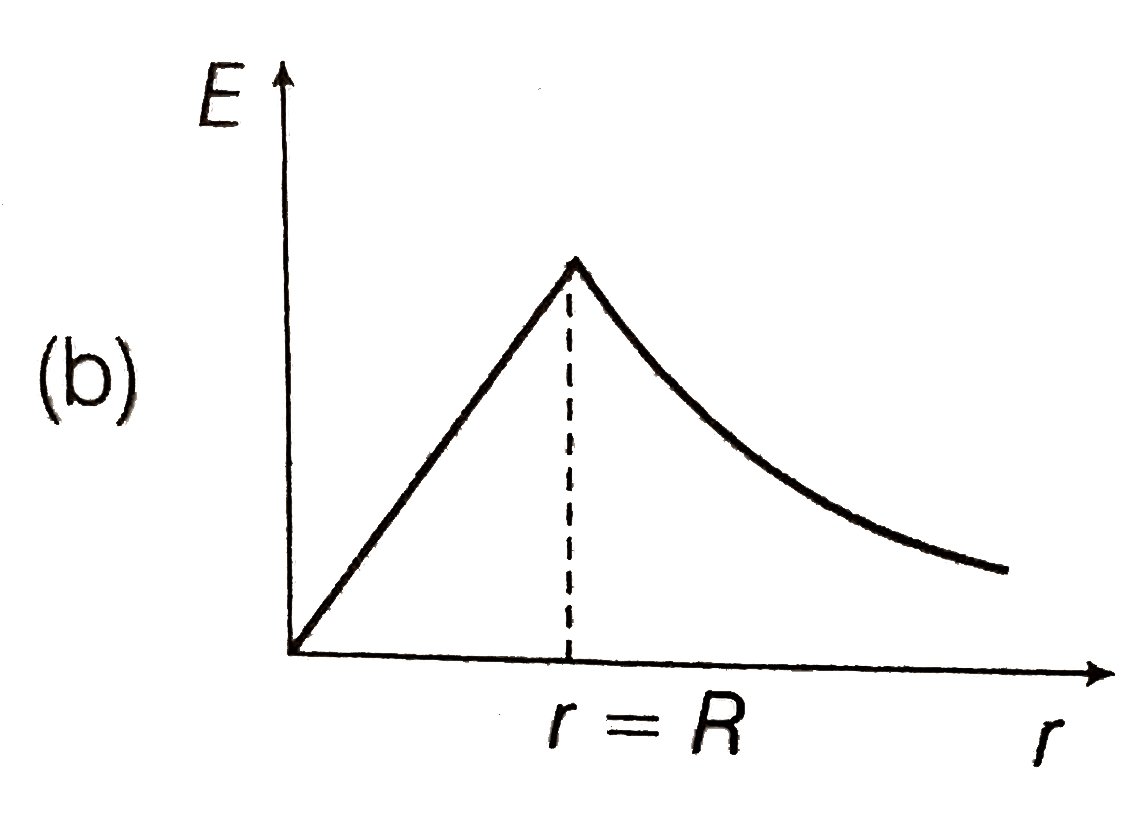 C
C D
D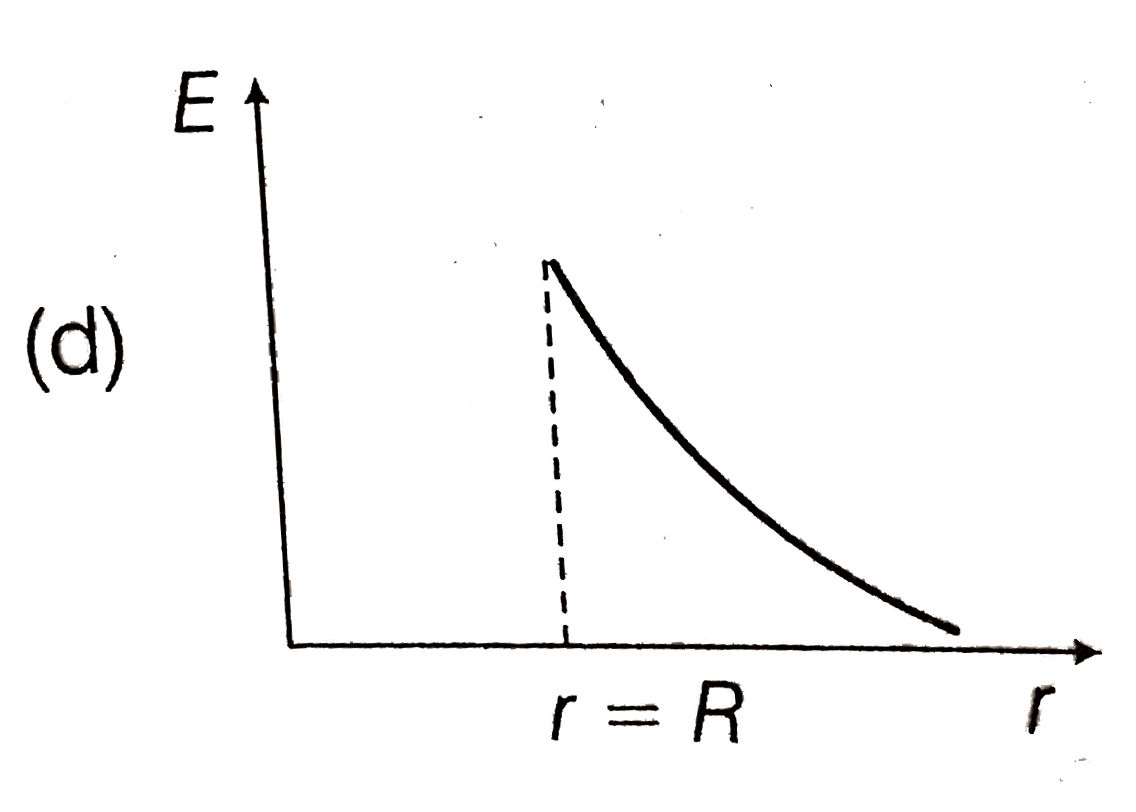
- Question 2 - Select One
A spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
Ainside is zero and varies as r−1 outside itBinside is constant and varies as r−2Cinside is zero and varies as r−2 outside itDinside is constant and varies as r−1 outside it - Question 3 - Select One
A charge Q is placed at the centre of a spherical conducting shell. Choose the correct option.
AOnly −Q will appear on its inner surfaceBOnly +Q will appear on its outer surfaceCA charge −Q will appear on its surface and +Q on its outer surfaceDA charge +Q will appear on its inner surface and −Q on its outer surface
A spherical conducting shell of inner radius r1 and outer radius r2 has a charges 'Q' A charges 'q' is placed at the centre of the shell.
What is the surface charges density on the (i) inner surface (ii) outer surface of the shell?
(b) A spherical conducting shell of inner radius r1 and outer radius r2 has a charges 'Q' A charges 'q' is placed at the centre of the shell.
Write the expression for the electric field at a point x>r2 from the centre of the shell.View SolutionA thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge Q2 is placed at its centre C and another charge +2Q is placed outside the shell at point A at a distance x from the centre (x>R)
Find the force on the charge at the centre of the shell and at the point A
Find the electric flux through the shell.View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin metallic spherical shell contains a charge Q on it. A point charge q is placed at the center of the shell and another charge q1 is placed outside it as shown in figure. All the three charges are positive

The force on the charge at the centre isView SolutionA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?
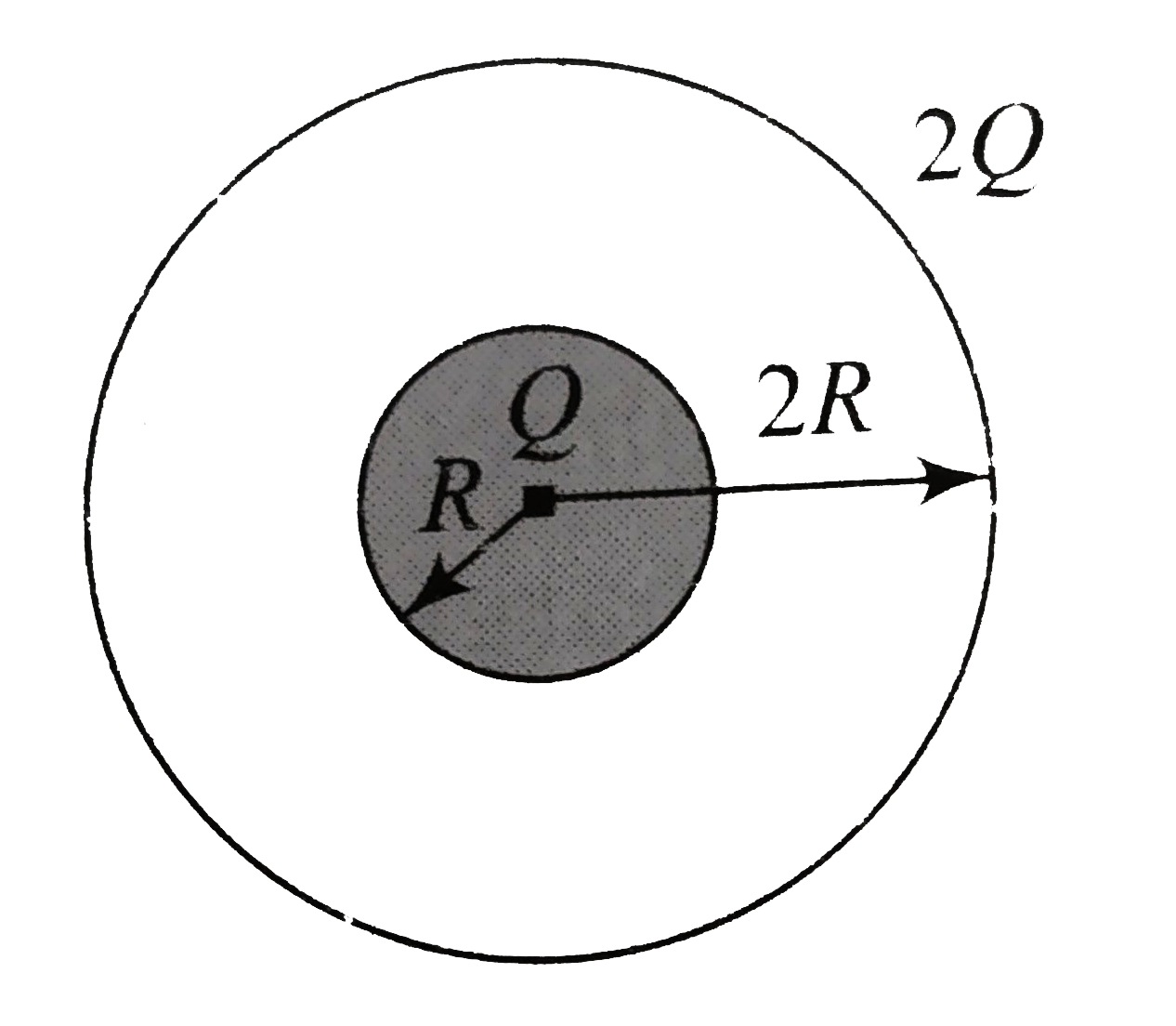 View Solution
View Solution
