A conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as




The correct Answer is:A
To solve the problem, we need to analyze the electric field E at different regions in relation to the conducting shell and the point charge. We will use Gauss's law to determine how the electric field varies with distance r from the center of the shell.
1. Identify the System:
- We have a conducting shell of radius R with a charge of −Q.
- A point charge +Q is placed at the center of the shell.
2. Determine the Electric Field Inside the Shell:
- For r<R (inside the conducting shell), we consider a Gaussian surface that is a sphere of radius r (where r<R).
- The only charge enclosed by this Gaussian surface is the point charge +Q.
- According to Gauss's law:
Φ=Qencϵ0
- Here, Qenc=+Q, so:
Φ=Qϵ0
- The electric flux Φ can also be expressed as:
Φ=E⋅A=E⋅4πr2
- Setting these equal gives:
E⋅4πr2=Qϵ0
- Solving for E:
E=Q4πϵ0r2
- Thus, the electric field inside the shell (for r<R) varies as:
E∝1r2
3. Determine the Electric Field on the Surface of the Shell:
- At r=R, we can use the same formula:
E=Q4πϵ0R2
4. Determine the Electric Field Outside the Shell:
- For r>R, we consider a Gaussian surface outside the shell.
- The total charge enclosed by this Gaussian surface is +Q (from the point charge) and −Q (from the shell), resulting in a net charge of 0.
- Therefore, according to Gauss's law:
Φ=Qencϵ0=0
- This implies:
E⋅4πr2=0⟹E=0
- Thus, for r>R, the electric field is:
E=0
5. Summarize the Results:
- For r<R: E∝1r2
- For r=R: E=Q4πϵ0R2
- For r>R: E=0
Conclusion:
The electric field E varies with distance r as follows:
- It decreases with 1r2 for r<R.
- It is constant at Q4πϵ0R2 at r=R.
- It becomes zero for r>R.
- We have a conducting shell of radius R with a charge of −Q.
- A point charge +Q is placed at the center of the shell.
- For r<R (inside the conducting shell), we consider a Gaussian surface that is a sphere of radius r (where r<R).
- The only charge enclosed by this Gaussian surface is the point charge +Q.
- According to Gauss's law:
Φ=Qencϵ0
- Here, Qenc=+Q, so:
Φ=Qϵ0
- The electric flux Φ can also be expressed as:
Φ=E⋅A=E⋅4πr2
- Setting these equal gives:
E⋅4πr2=Qϵ0
- Solving for E:
E=Q4πϵ0r2
- Thus, the electric field inside the shell (for r<R) varies as:
E∝1r2
- At r=R, we can use the same formula:
E=Q4πϵ0R2
- For r>R, we consider a Gaussian surface outside the shell.
- The total charge enclosed by this Gaussian surface is +Q (from the point charge) and −Q (from the shell), resulting in a net charge of 0.
- Therefore, according to Gauss's law:
Φ=Qencϵ0=0
- This implies:
E⋅4πr2=0⟹E=0
- Thus, for r>R, the electric field is:
E=0
- For r<R: E∝1r2
- For r=R: E=Q4πϵ0R2
- For r>R: E=0
The electric field E varies with distance r as follows:
- It decreases with 1r2 for r<R.
- It is constant at Q4πϵ0R2 at r=R.
- It becomes zero for r>R.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching
2 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA conducting spherical shell having inner radius a and outer radius b carries a net charge Q. If a point charge q is placed at the centre of this shell, then the surface charge density on the outer surface of the shell is given as:
View Solution
Knowledge Check
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
A(a) 2Q4πε0RB(b) 2Q4πε0R−2q4πε0RC(c) 2Q4πε0R+q4πε0RD(d) (q+Q)24πε0RA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
A2Q4πε0R−2q4πε0RB2Q4πε0R+q4πε0RC(q+Q)4πε02RD2Q4πε0RConsider a thin conducting shell of radius R carrying total charge Q. Two point charges Q and 2Q are placed on points A and B, which are at a distances of R2 and 2R from the center of the cell respectively as shown in the figure. If the cell is earthed how much charge will flow to the eart?
 A3QBQC2QDQ2
A3QBQC2QDQ2
A spherical conducting shell of inner radius r1 and outer radius r2 has a charges 'Q' A charges 'q' is placed at the centre of the shell.
What is the surface charges density on the (i) inner surface (ii) outer surface of the shell?
(b) A spherical conducting shell of inner radius r1 and outer radius r2 has a charges 'Q' A charges 'q' is placed at the centre of the shell.
Write the expression for the electric field at a point x>r2 from the centre of the shell.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
A charge q is placed at the centre of the shell. Find out the surface charge density on the inner and outer surface of the shell.
Is the electric field inside a cavity (with no charge ) zero. Independent of the fact wheather the shell is spherical or not ? Explain.
View SolutionA conducting shell has inner radius R and outer radius 2R. A charge + q is given to the spherical shell. (a) Find the electric field at a point which is at a distance x from the centre of the shell. Give your answer for three cases (i) x lt R (ii) R lt x lt 2R (iii) x gt 2R (b) Find the electric potential in all the three cases mentioned in (a) (c) Find field and potential in all the three cases mentioned in (a) after a point charge – q is introduced at the centre of the shell. (d) Write the electrical potential energy of the system consisting of the shell and the point charge at its centre. (e) Find the electrostatic force that the shell exerts on the point charge. (f) Now, another point charge + q is placed at a distance 4R from the centre of the shell. Find electric field and potential in following cases. (i) x lt R (ii) R lt x lt 2R
View SolutionConsider an initially neutral hollow conducting spherical shell with inner radius r and outer radius 2r. A point charge +Q is now placed inside the shell at a distance r/2 from the centre. The shell is then grounded by connecting the outer surface to the earth. P is an external point at a distance 2r from the point charge +Q on the line passing through the centre and the point charge +Q as shown in the figure.
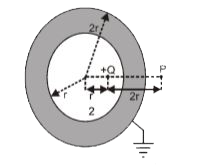
The magnitude of the force on a test charge +q placed at P will be
View Solution
