A small ball thrown at an initial velocity v0 at an angle α to the horizontal strikes elastically with a smooth vertical wall moving towards it at a horizontal velocity v and returns to the point from which it was thrown. Determine the time t from the beginning of motions to the moment of impact with vertical wall. Neglect friction losses.
t=v0sinα(v0cosα+2v)g(v0cosα+v)
t=v0sinα(v0cosα−2v)g(v0cosα+v)
t=v0sinα(v0cosα+2v)g(v0cosα−v)
t=v0cosα(v0sinα+2v)g(v0sinα+v)
The correct Answer is:A
Since the wall is smooth, the impact against the wall does not alter the vertical component of the ball velocity. Therefore the total time t1 of motion of the ball is the total time of the ascent and descent of the body thrown upwards at a velocity v0sinα in the gravitational field. Consequently t1=2v0sin(α)g. The motion of the ball along the horizontal is the sum of two motions Before the collision with the wall it moves at a velocity v0cosα+v. Since the impact is perfectly elastic, the ball moves away from the wall after the collision at a velocity v0cosα+v. Therefore the ball has the following horizontal velocity relative tot he ground
(v0cosα+v)+v=v0cosα+2v.
If the time of motion before the impact is t. By equating the distance covered by the ball before ad after te collision, we obtain the following equation:
v0cosαα.t=(t1−t)(v0cosα+2v)
since the total time of motion of the ball is t1=2v0sin(α)g. we find the thhat
t=v0sinα(v0cosα+2v)g(v+(0)cosα+v)
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A ball is projected with velocity v0 at an angle α to the horizonal, towards a smooth wall which appraches the ball. With velocity u. After collision the ball retraces its path to the point of projection . What is the time t taken by the ball form the instant of projection to point of impact ?

View SolutionA particle of mass m and charge q is thrown with initial velocity v0 at an angle with the horizontal. In space there exist an electric field of strength E at angle β with the downward vertical away from the point of projection. Find the time of flight and range of projectile on horizontal ground
View Solution
Knowledge Check
A projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
Av0sinα vertically downwardB2v0sinα vertically downwardC2v0sinα vertically upwardDzeroA projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
Av0Bv0sinαCv0cosαD√gR2A girl throws a ball with an initial velocity v at an angle 45∘. The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebound returns to her hands. What is the coefficient of restitution between wall and ball ? (v2>dg)
Av2−gdgdBgdv2−gdCgdv2Dv2gd
A particle is thrown vertically upwards with a velocity v. It returns to the ground in time T. which of the following graphs correctly represents the motion ?
View SolutionA ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collision with a vertical wall and returns to ground. The total time of flight of the ball is
View SolutionA ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collison with a vertical wall and returns to ground. The total time of flight of the ball is
View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
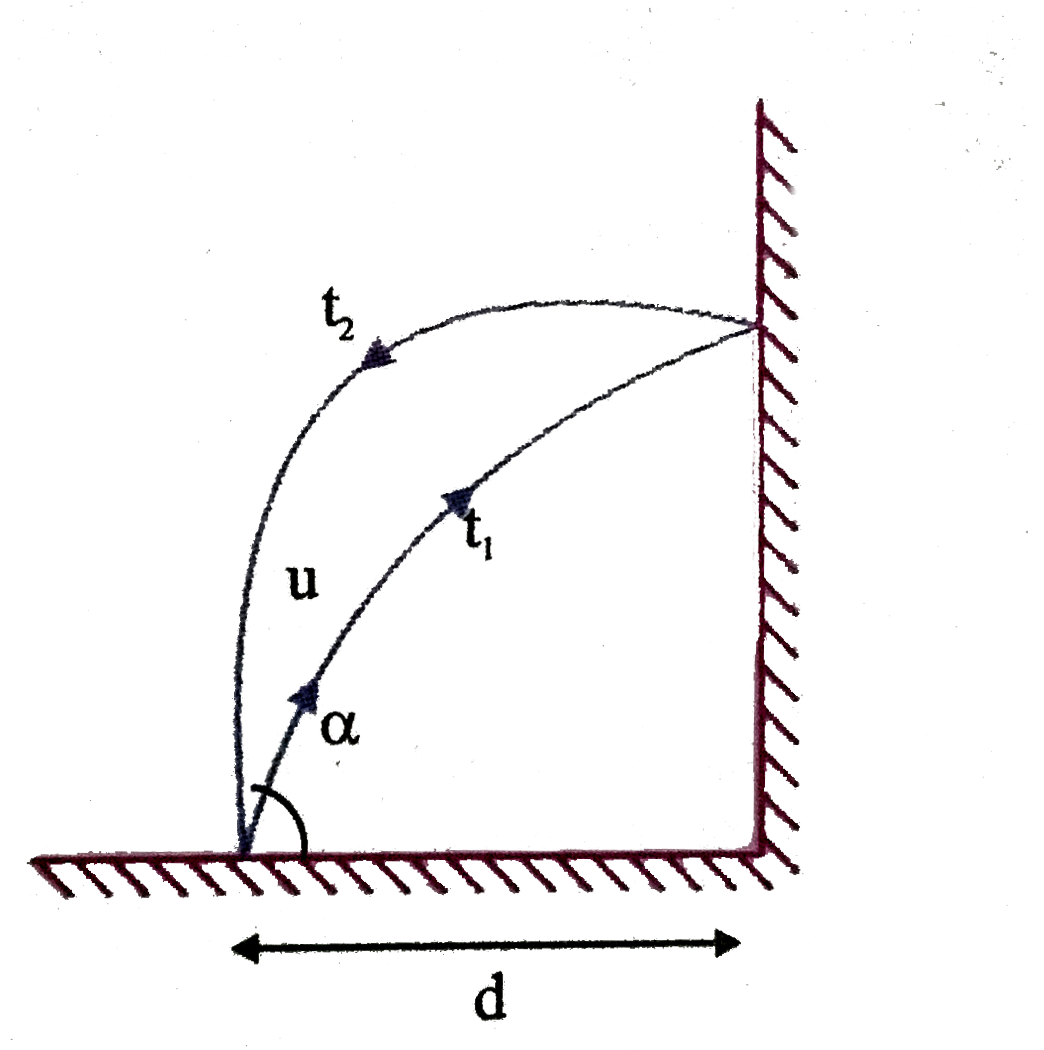
If the line joining the point of projection and the point of impact makes an angle 'θ' with the horizontal, then tanθ is
View Solution
