Tension in a uniform string of length L varies with length uniformly. At one end A tension is T0 and at other end B it is 16T0. If mass per unit length of string is μ. Choose the correct options (s)
Time taken by a pulse to move from end A and B is 25L√μT0
Time taken by a pulse to move from end A to end B is 215√μLT0(√15−1)
Tension in the string as function of distance x from end A is T=T0+15T0Lx
Tension in the string as function of distance x from end A is T=T0+15T0Lx
The correct Answer is:A, C
V=dxdt
⇒dt=dxV=∫L0dx√T0+15T0L.xμ
t=25√μL2T0
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Pt-02
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 107 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
The mass of an uniform ladder of length l increases uniformly from one end A to the other end B,
find the position of the centre of mass from end A.
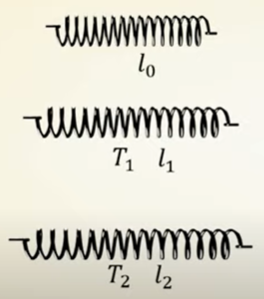
View SolutionA spring with natural length l0 has a tension T1 when its length is l1 and the tension is T2 when its length is l2.The natural length of spring will be:
View Solution
Knowledge Check
A perfectly straight portion of a uniform rope has mass M and length L. At end A of the segment, the tension in the rope is TA and at end B it is TB(TB>TA). Neglect effect of gravity and no contact force acts on the rope in between points A and B. The tension in the rope at a distance L/5 from end A is:-
ATB−TAB(TA+TB)/5C(4TA+TB)/5D(T1−TB)/5The stirng stretched by tension T and length L vibrates in resonance with a tuning fork of frequency n. the tension in the stretched string is increased by 69% and length of string reduced by 35%. Then, the frequency of vibrating string is
AnB1.5nC2nDn2A perfectly straight portion of a uniform rope has mass M and length L . At end A of the segment, the tension in the rope is TA and at end B it is TB(TB>TA . Neglect effect of gravity and no contact force acts on the rope in between points A and B . The tension in the rope at a distance L/5 from end A is.
ATB−TAB(TA+TB)/5C(4TA+TB)/5D(TA−TB)/5
A light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are μ and 9μ and the tension is T. Find the possible values of frequencies such that junction of two wire point A is a node.

View SolutionThe frequency f of vibration of a string between two fixed ends is proportional to LaTbμc, where L is the length of string, T is tension in the string and mu is the linear mass density (or mass per unit length) of string. Find the value of a,b and c.
View SolutionDerive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
View SolutionThe frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionOne end of a string of length L is tied to the ceiling of a lift acceleration upwards with an acceleration 2g. The other end of the string is free. The linear mass density of the string varies linearly from 0→λ from bottom to top. Choose the correct option(s)
View Solution

