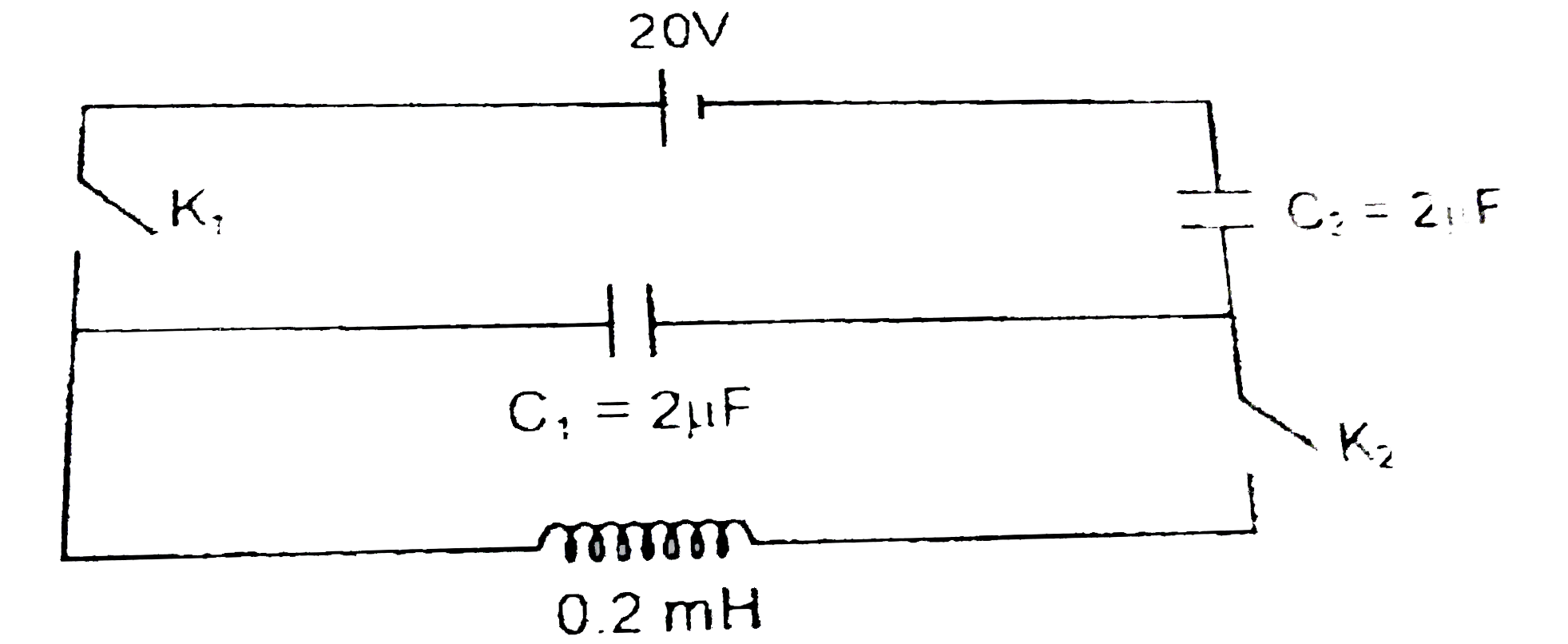
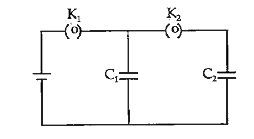
A circuit containing two capacitor C1 and C2 shown in figure is in steady state with switch K1 closed and K2 open. At the instant t=0,K1 is opened and K2 is closed. The correct statements are.
Angular frequency of oscillation of LC circuit is 5×104radsec
charge on capacitor C1 at t=0 is 40μC
Maximum current in iductor is 1A
Charge on capacitor C1 is 10√3μC when energy in the inductor becomes one third of the energy in capacitor.
The correct Answer is:A, C, D
ω=1√LC=5×104radsec
q=CeqV=1×10−6×20=20μC
Imax=ωqmax=5×10−4×20×10−6=1A
UC+UL=Utotal
UC+UC3Utotal
UC=34UTotal
q22C=34(qmax)22C
q=√32×20μC=10√3μC
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
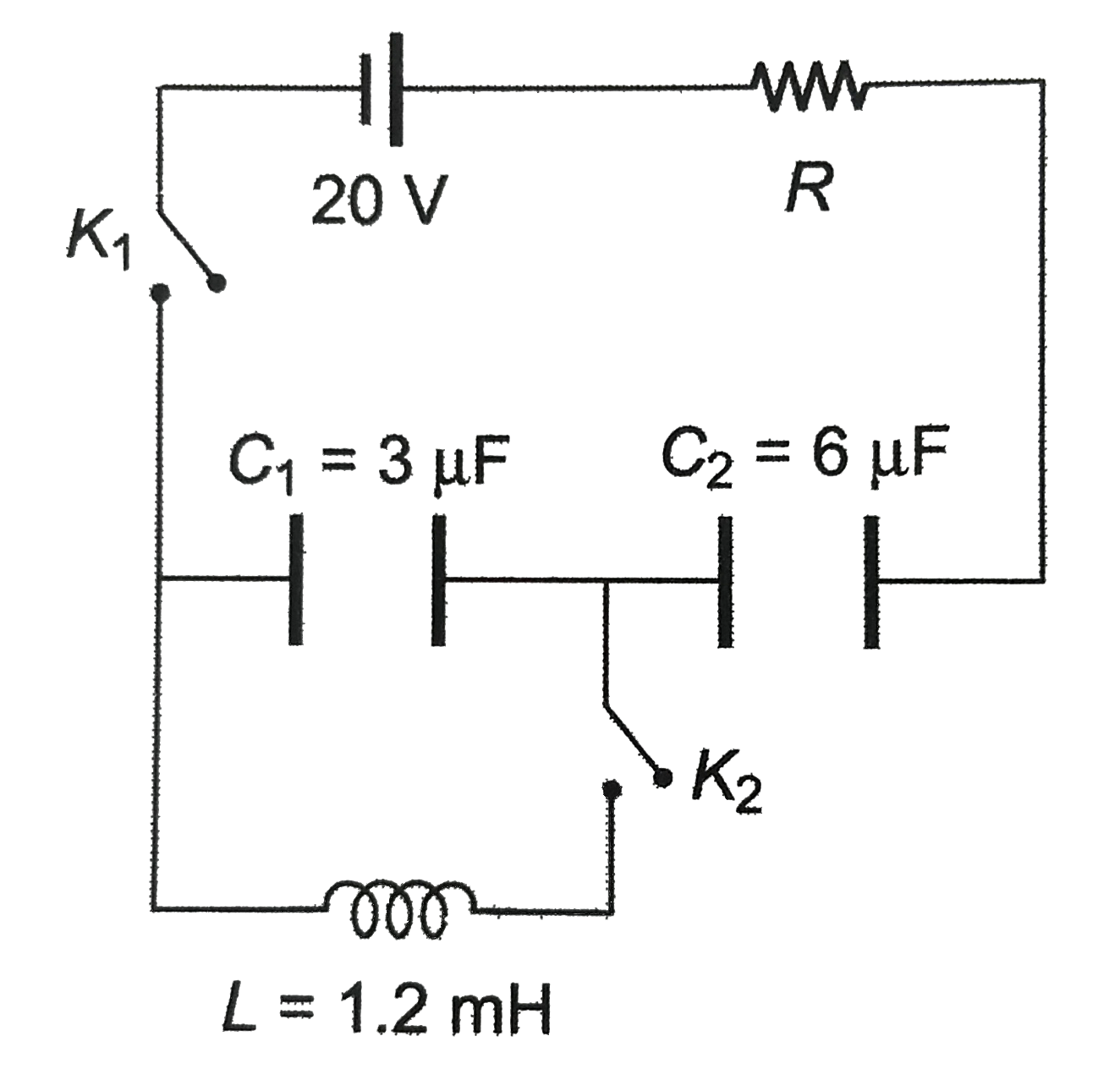
A circuit containing capacitors C1 and C2 shown in the figure is in the steady state with key K1 cloesed. At the instant t=0 , K1 is opened and K2 is closed.
(a) Find the angular frequency of oscillation of the LC circuit.
(b) Determine the first instant t , when enregy in the indctor becomes one third of that in the capacitor.
(c) Calculate the change on the plates of the capacitor at that instant.
View SolutionA circuit containing capacitors C1 and C2, shown in the figure is in the steady state with key K1 and K2 opened. At the instant t=0, K1 is opened and K2 is closed.
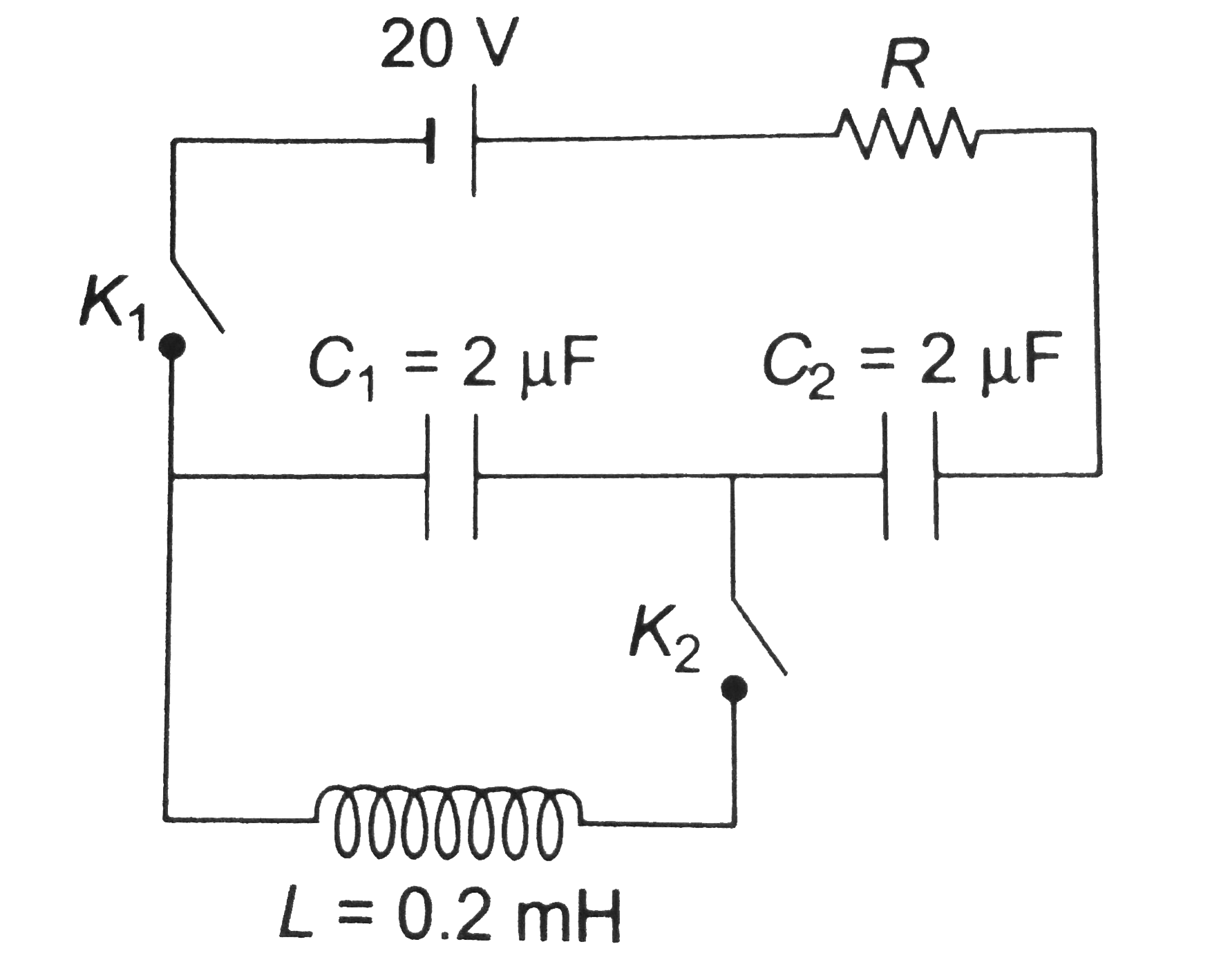
(a) Find the angular frequency of oscillations of L−C circuit.
(b) Determine the first instant t, when energy in the inductor becomes one third of that in the capacitor.
(c) Calculate the charge on the plates of the capacitor at that instant.
View Solution
Knowledge Check
A circuit containing capacitors C1andC2 shown in Fig. is in the steady state with key K1 closed. At the instant t = 0, K1 is opened and K2 is closed. The angular frequency of oscillation of the circuit and charge across C1att=125(μ)s are respectively
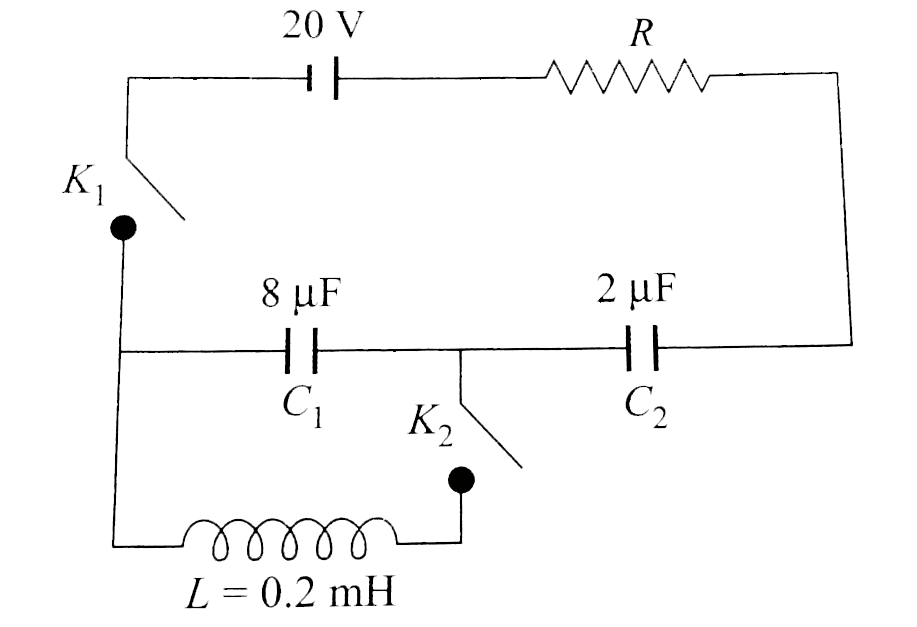 A25×103rads−1,32(μ)CB5×104rads−1,16(μ)CC5×104rads−1,−16(μ)CD25×103rads−1,−32(μ)C
A25×103rads−1,32(μ)CB5×104rads−1,16(μ)CC5×104rads−1,−16(μ)CD25×103rads−1,−32(μ)CIn the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are
 Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2In the circuit as shown in figure the switch is closed at t=0.

At the instant of closing the switchAthe battery delivers maximum currentBno current flows through CCvoltage drop across R2 is zeroDthe current through the battery decreases with time finally becomes zero
In the circuit shown in Figure, initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed. Then
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed. At t=0, S1 is opened and switch S2 is closed.
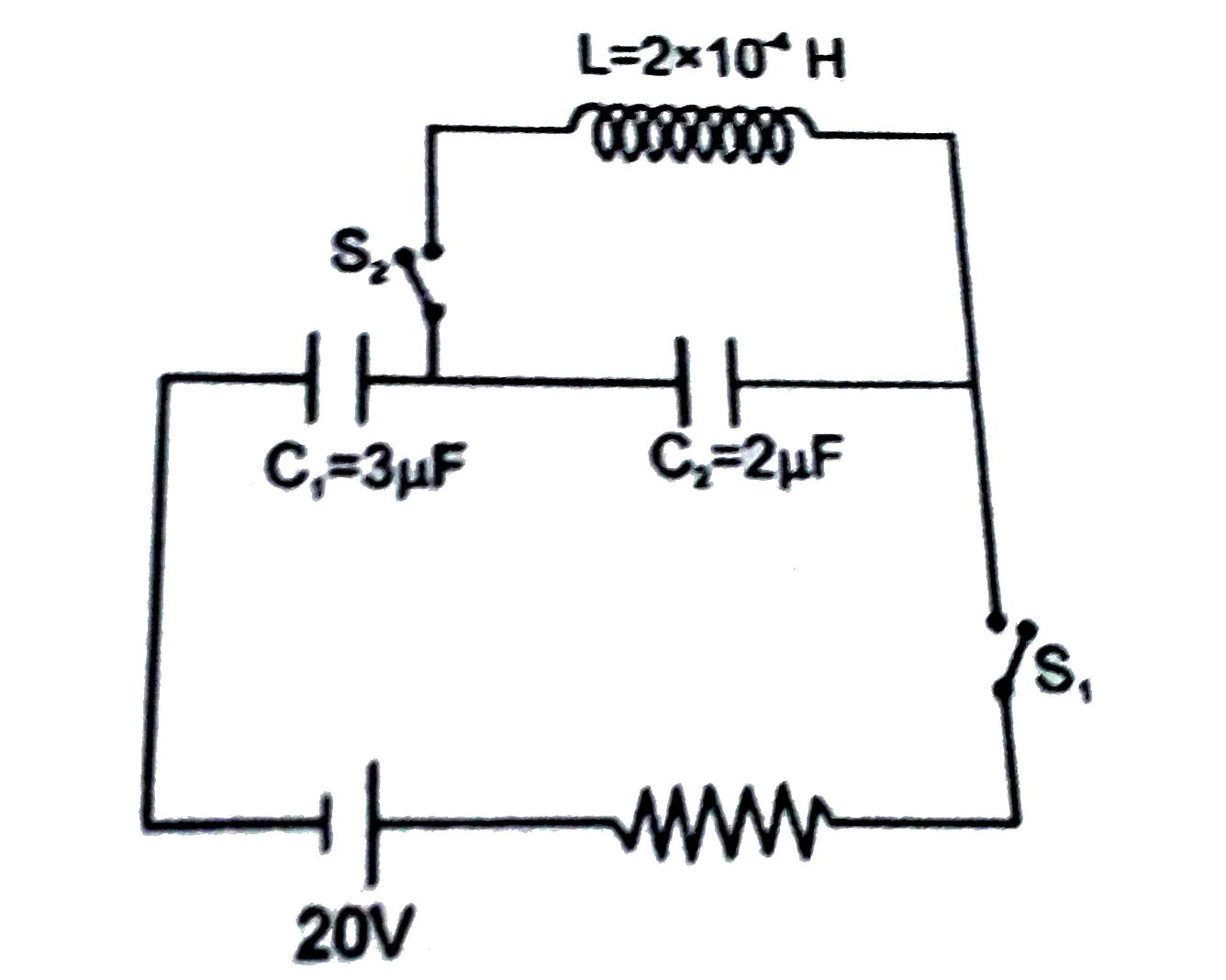
Find the first instant t, when energy in inductor becomes one third of that in capacitor
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed.At t=0,S1 is opened and switch S2 is closed. The first instant t when energy in inductor becomes one third of that in capacitor is equal to π×10−5xsec. Then finout value of x.
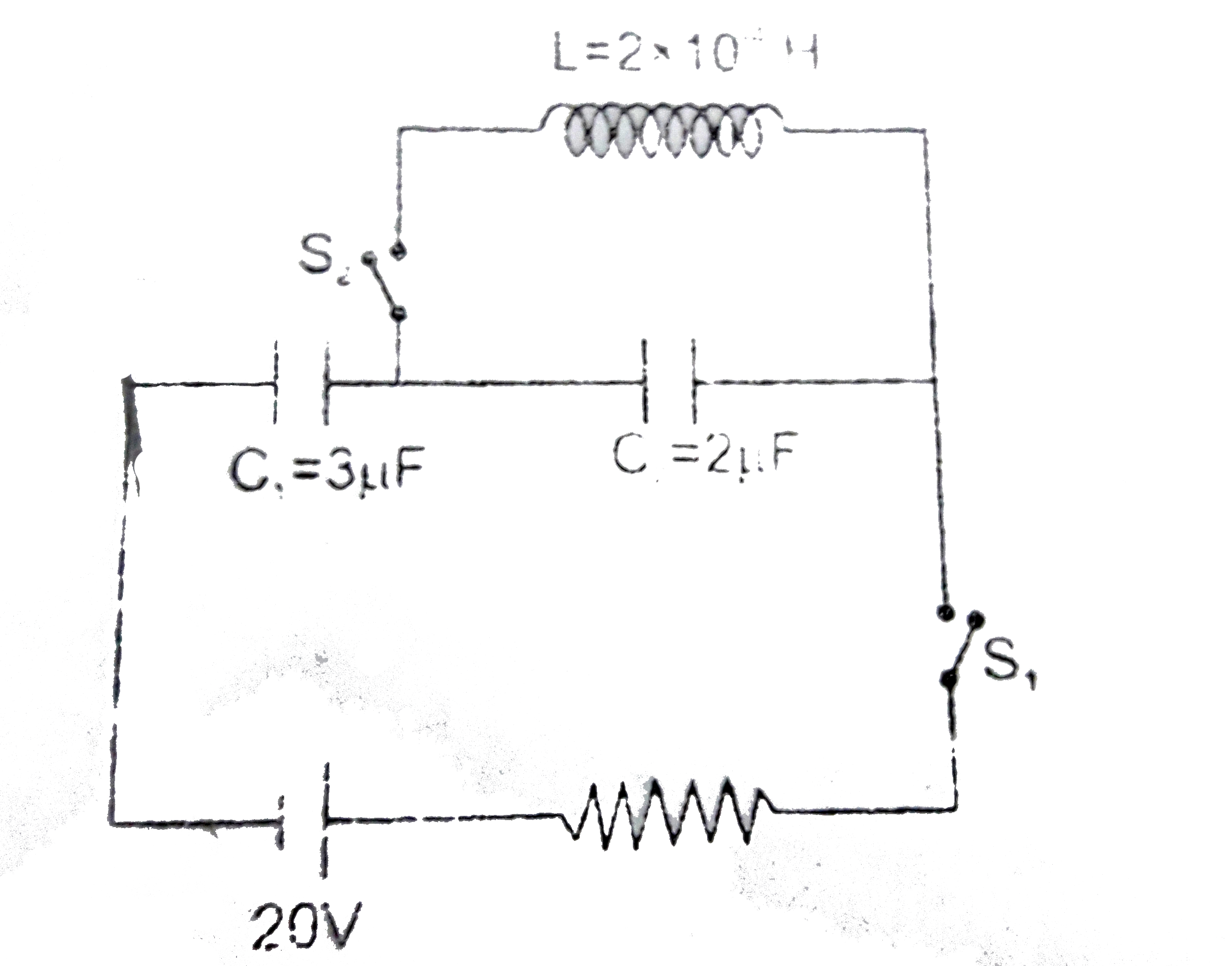
View SolutionThe circuit shows in Fig. is in the steady state with switch S1 closed. At t=0,S1 is opened and switch S2 is closed.
a. Derive expression for the charge on capacitor C2 as a function of time.
b. Determine the first instant t, when the energy in the inductor becomes one-third of that in the capacitor.

View SolutionThe circuit consists of two resistors (of resistance R1=20Ω and R2=10Ω), a capacitor (of capacitance C=10μF) and two ideal cells. In the circuit shown the capacitor is in steady state and the switch S is open
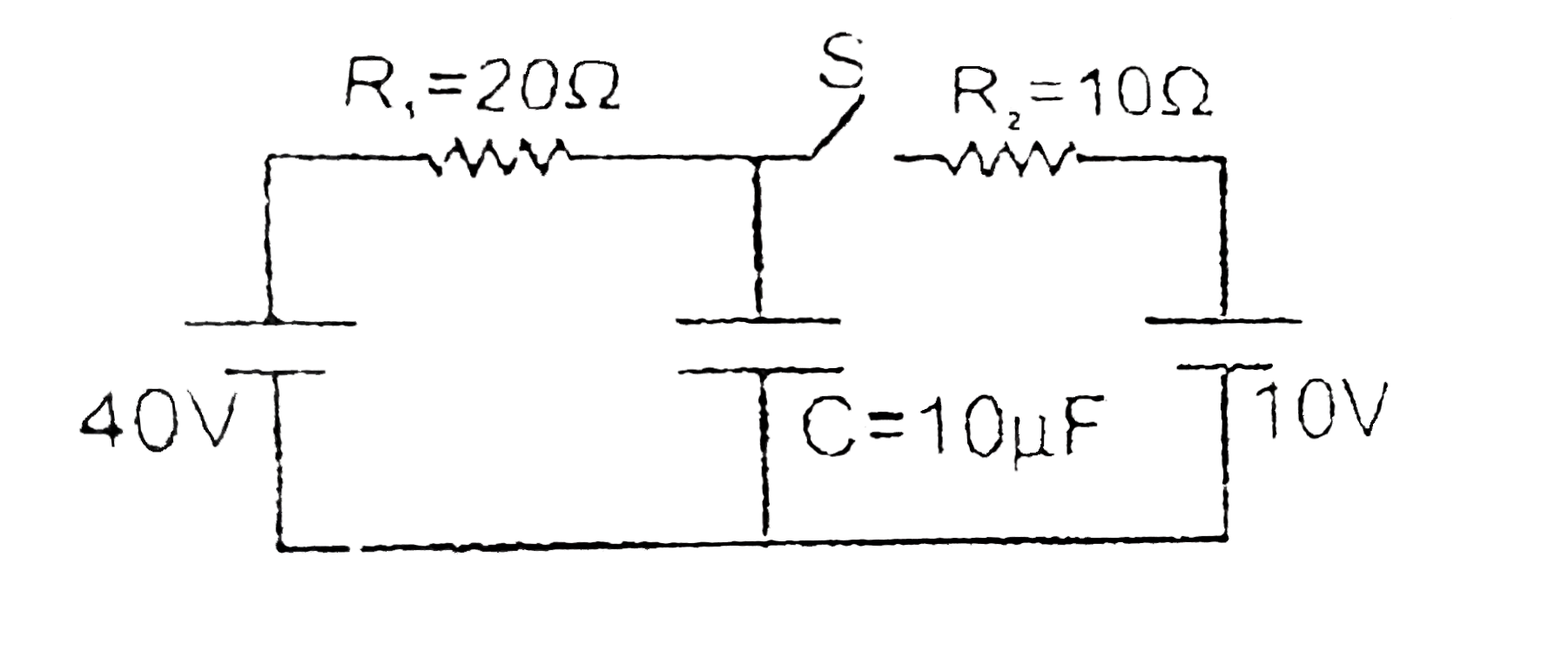
the circuit is in steady state with switch S closed. Now the switch S is opened. Just after the switch S is opened. the current through resistance R1 is
View Solution
