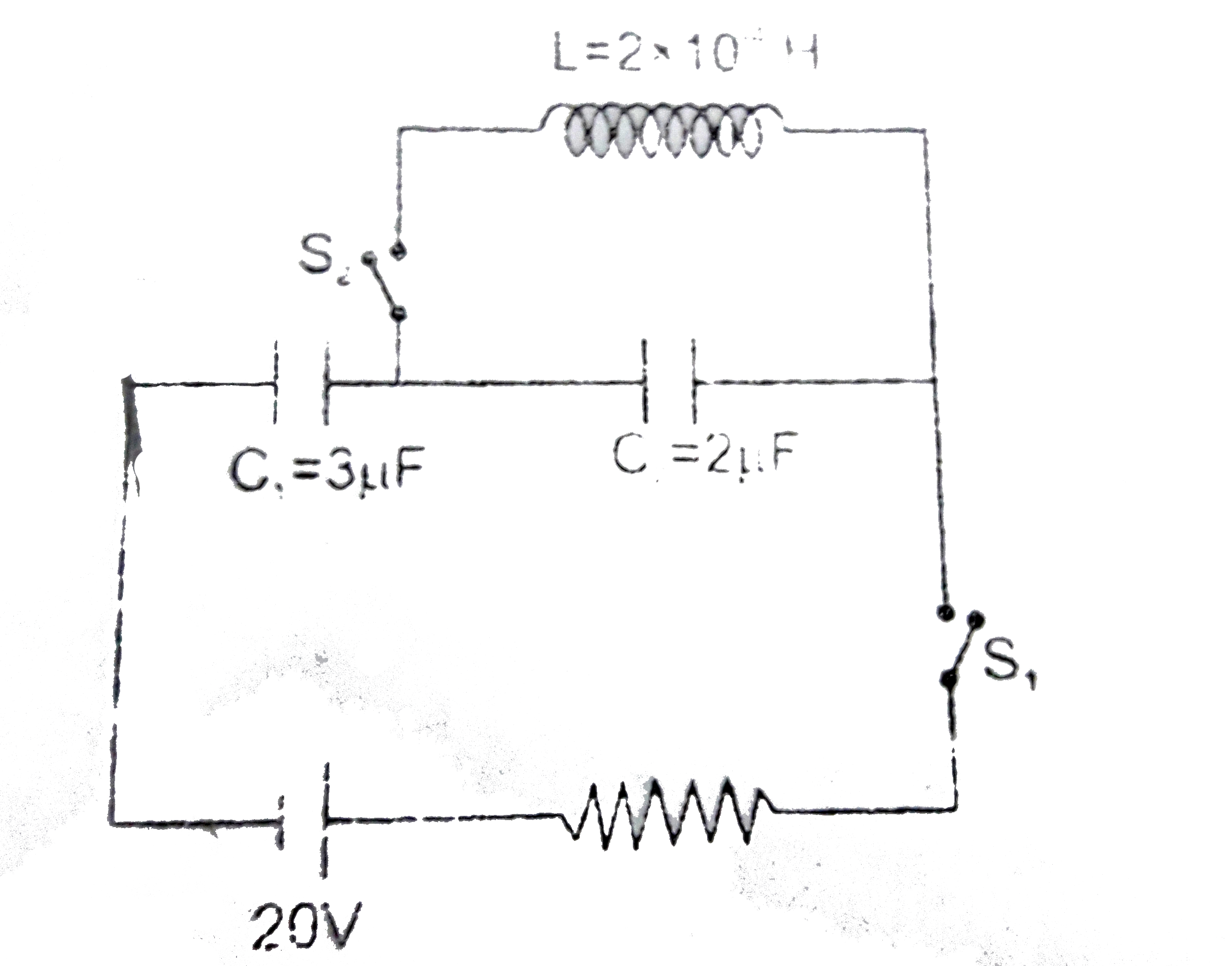
A circuit containing capacitors C1 and C2, shown in the figure is in the steady state with key K1 and K2 opened. At the instant t=0, K1 is opened and K2 is closed.
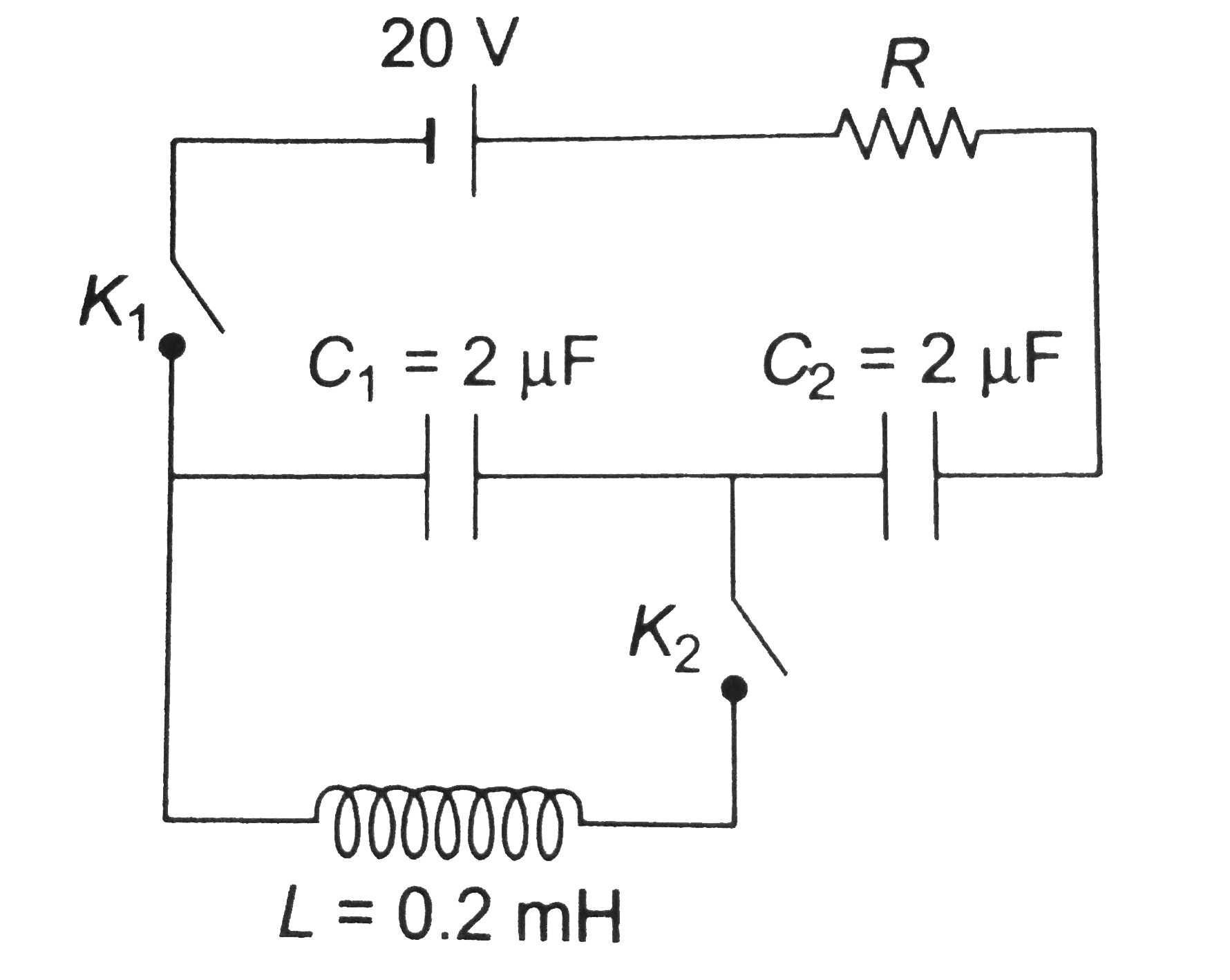
(a) Find the angular frequency of oscillations of L−C circuit.
(b) Determine the first instant t, when energy in the inductor becomes one third of that in the capacitor.
(c) Calculate the charge on the plates of the capacitor at that instant.
The correct Answer is:A, C
With key K1 closed C1 and C2 are in series with the battery in steady state.
∴Cnet=1μF or q0=CnetV=20μC
a. With K1 opened and K2 closed, charge on C2 will remain as it is while charge on C1 will oscillate in L−C1 circuit.
ω=1√LC1
=1√0.2×10−3×2×10−6
=5×104rad/s
b. Since at t=0, charge is maximum (=q0)
Therefore, current will be zero.
12Li2=13(12q2C)
or i=q√3CL=qω√3
From the expression
i=ω√q20−q2
We have qω√3=ω√q20−q2
or q=√32q0
Since at t=0 charge is maximum or q0, so we can write
q=q0cosωt or √3q02=q0cosωt
or ωt=π6 or t=π6ω=π6×5×104
=1.05×10−5s
c. q=√32q0=√32=×20=10√3μC
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
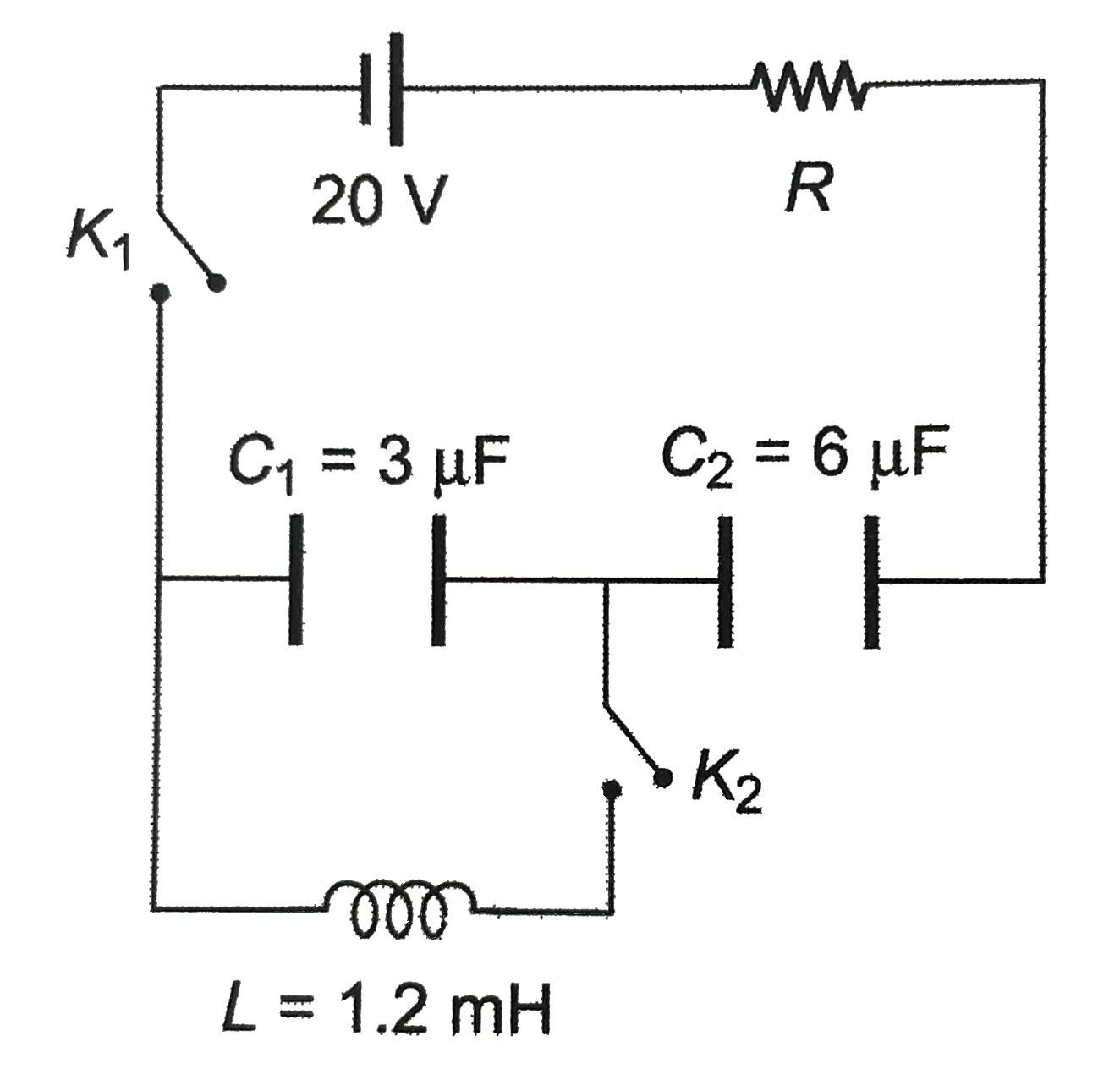
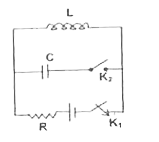
A circuit containing capacitors C1 and C2 shown in the figure is in the steady state with key K1 cloesed. At the instant t=0 , K1 is opened and K2 is closed.
(a) Find the angular frequency of oscillation of the LC circuit.
(b) Determine the first instant t , when enregy in the indctor becomes one third of that in the capacitor.
(c) Calculate the change on the plates of the capacitor at that instant.
View SolutionThe circuit shows in Fig. is in the steady state with switch S1 closed. At t=0,S1 is opened and switch S2 is closed.
a. Derive expression for the charge on capacitor C2 as a function of time.
b. Determine the first instant t, when the energy in the inductor becomes one-third of that in the capacitor.

View Solution
Knowledge Check

A circuit containing two capacitor C1 and C2 shown in figure is in steady state with switch K1 closed and K2 open. At the instant t=0,K1 is opened and K2 is closed. The correct statements are.AAngular frequency of oscillation of LC circuit is 5×104radsecBcharge on capacitor C1 at t=0 is 40μCCMaximum current in iductor is 1ADCharge on capacitor C1 is 10√3μC when energy in the inductor becomes one third of the energy in capacitor.A circuit containing capacitors C1andC2 shown in Fig. is in the steady state with key K1 closed. At the instant t = 0, K1 is opened and K2 is closed. The angular frequency of oscillation of the circuit and charge across C1att=125(μ)s are respectively
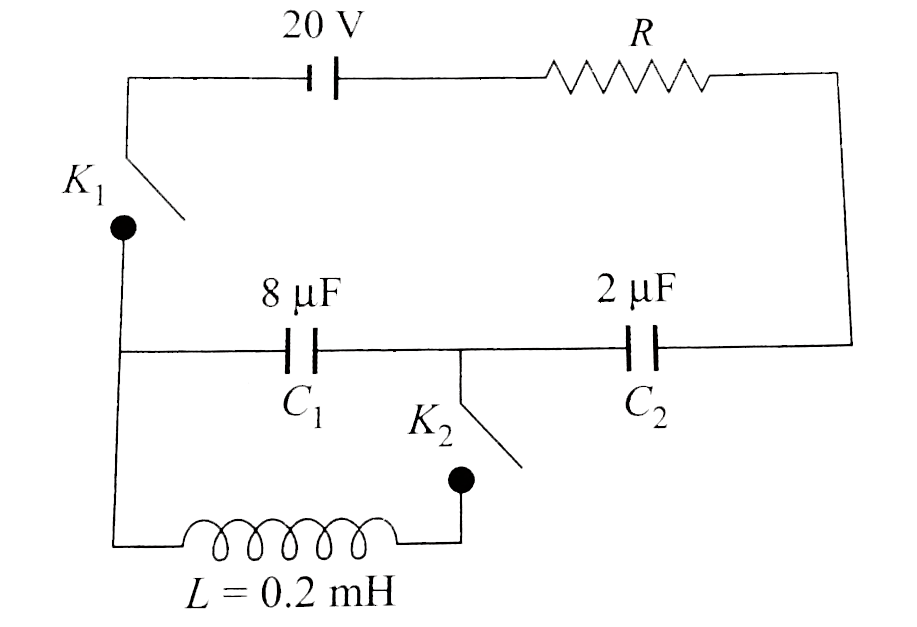 A25×103rads−1,32(μ)CB5×104rads−1,16(μ)CC5×104rads−1,−16(μ)CD25×103rads−1,−32(μ)C
A25×103rads−1,32(μ)CB5×104rads−1,16(μ)CC5×104rads−1,−16(μ)CD25×103rads−1,−32(μ)CShown in the figure is an R−L circuit. Just after the key (K) is closed
 Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
The circuit shown in figure is in the steady state with switch S1 closed. At t=0, S1 is opened and switch S2 is closed.

Find the first instant t, when energy in inductor becomes one third of that in capacitor
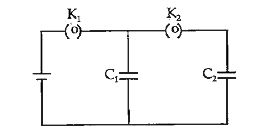
View SolutionIn the circuit shown in Figure, initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed. Then
View SolutionFigure-5.150 shows LC circuit with initial charge on capacitor 200μC. If at t=0 switch is closed, find the first instant when energy stored in inductor becomes one third that of capacitor.

View SolutionThe circuit shown in figure is in the steady state with switch S1 closed.At t=0,S1 is opened and switch S2 is closed. The first instant t when energy in inductor becomes one third of that in capacitor is equal to π×10−5xsec. Then finout value of x.
View SolutionShown in the figure is a parallel R , L,C circuit with key K1 closed and K2 opened . When K1 is opened and K2 is closed simultaneously find the maximum potential difference across the capacitor and maximum charge stored in it .
View Solution
