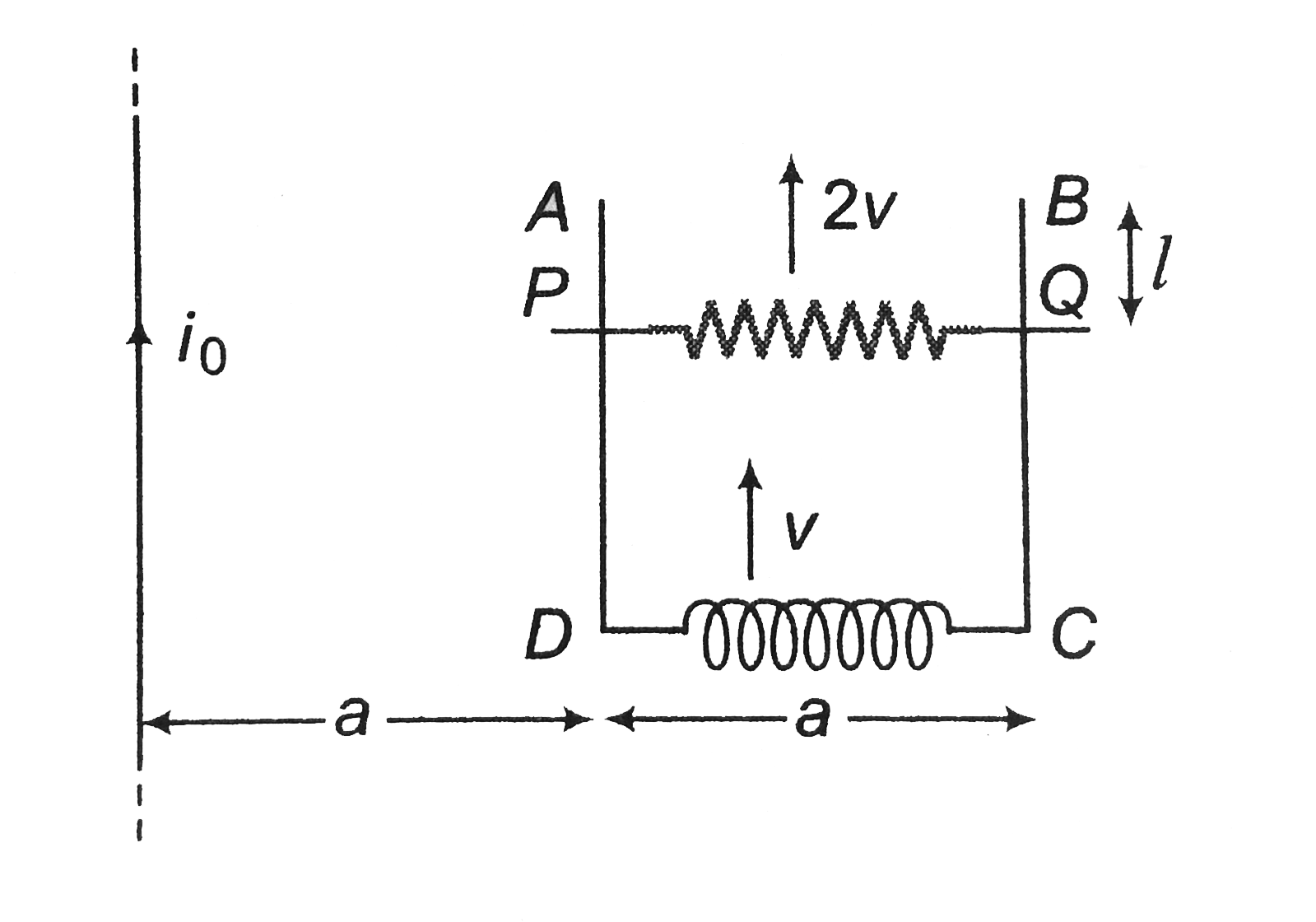
U-frame ABCD and a sliding rod PQ of resistance R, start moving with velocities v and 2v respectively, parallel to a long wire carrying current i0. When the distance AP=1 at t=0, determine the current through the inductor of inductance L just before connecting rod PQ loses contact with the U-frame.
The correct Answer is:B
Since PQ and DC both cut the lines of field.
∴ motional emf will be indued across both of them.
Integrating, potential difference across
dx⇒∫de=∫2vavμ0i02πxdx
eDc=vμ0i02π ln 2 with D at higher potential
ePQ=2vμ0i02π ln 2 with P at higher potential
The relative velocity of the rod PQ w.r.t U frame
Now relative velocity of the rod PQ w.r.t U frame
vnet=2v−v=v
Now, time taken by its to loose the contact t=lv

From equivalent electrical network
Net emf in the closed loop QPDC.
e=ePQ=eDC=vμ0i02πln2
Growth of current in the L−R circuit is given by
i=i0(1−e−tL)=(eR)(1−e−tRL)
At time t=lv
⇒i=(eR)(1−e−RlvL)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Video
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View Solution
Knowledge Check
A frame a bed and a sliding rod PQ of resistance R, start moving with the velocities v and 2v respectively parallel to a long wire carrying steady current I, as shown in the figure.
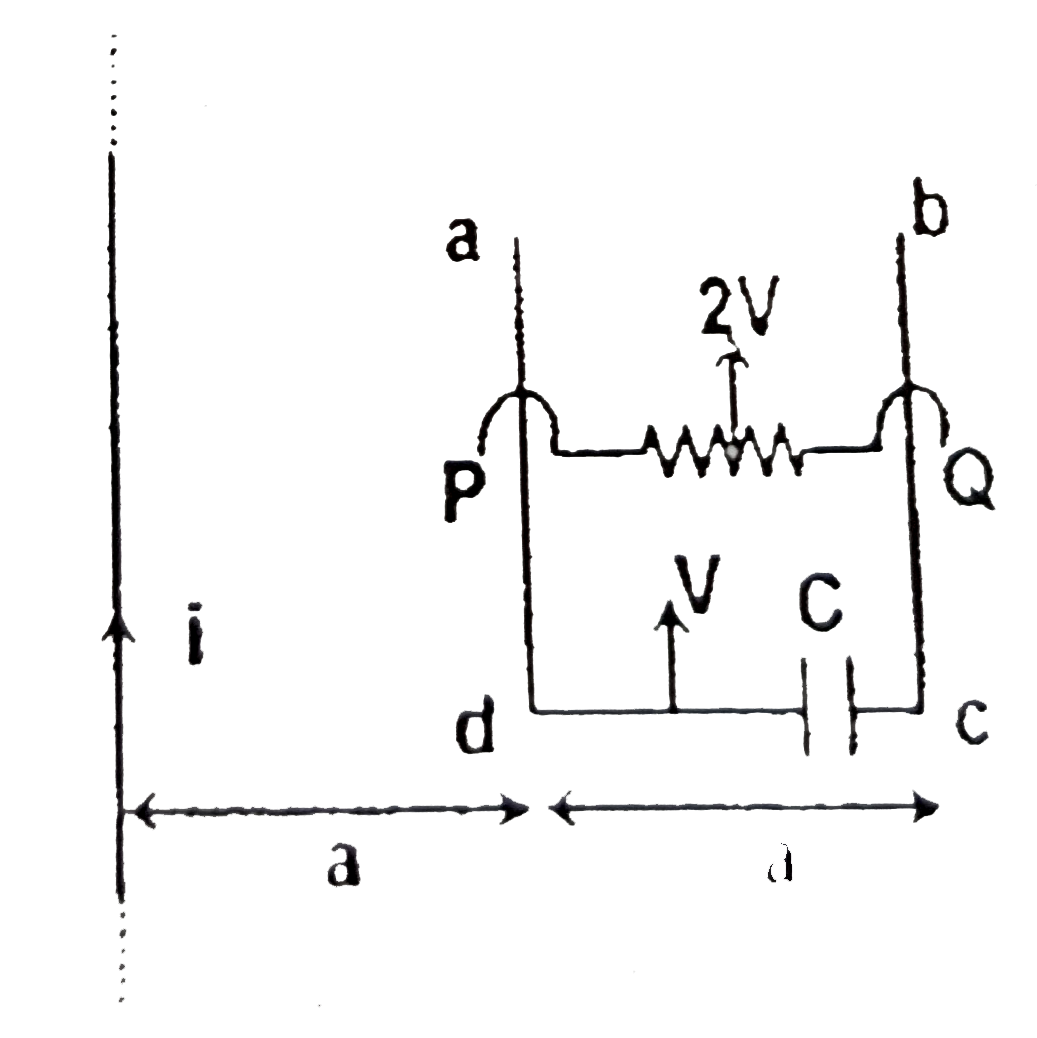 Acharge on the capacitor at time t is q=Cμ0ivln22π[1−e−t/RC]Bcharge on the capacitor at time t is q=Cμ0ivln2π[1−e−t/RC]Ccurrent passing through the resistor at time t is i=μ0ivln22πR[e−t/RC]Dcurrent passing through the capcitor at time t is i=μ0ivln2πR[e−t/RC]
Acharge on the capacitor at time t is q=Cμ0ivln22π[1−e−t/RC]Bcharge on the capacitor at time t is q=Cμ0ivln2π[1−e−t/RC]Ccurrent passing through the resistor at time t is i=μ0ivln22πR[e−t/RC]Dcurrent passing through the capcitor at time t is i=μ0ivln2πR[e−t/RC]The magnetic field at a distance r from a long wire carrying current i is 0.4 T. The magnetic field at a distance 2r is
A0.2 TB0.8TC0.1 TD1.6 TShows a copper rod moving with velocity v parallel to a long straight wire carrying current =100A. Calculate the induced emf in the rod, where v=5mS−1, a=1cm , b=100cm.
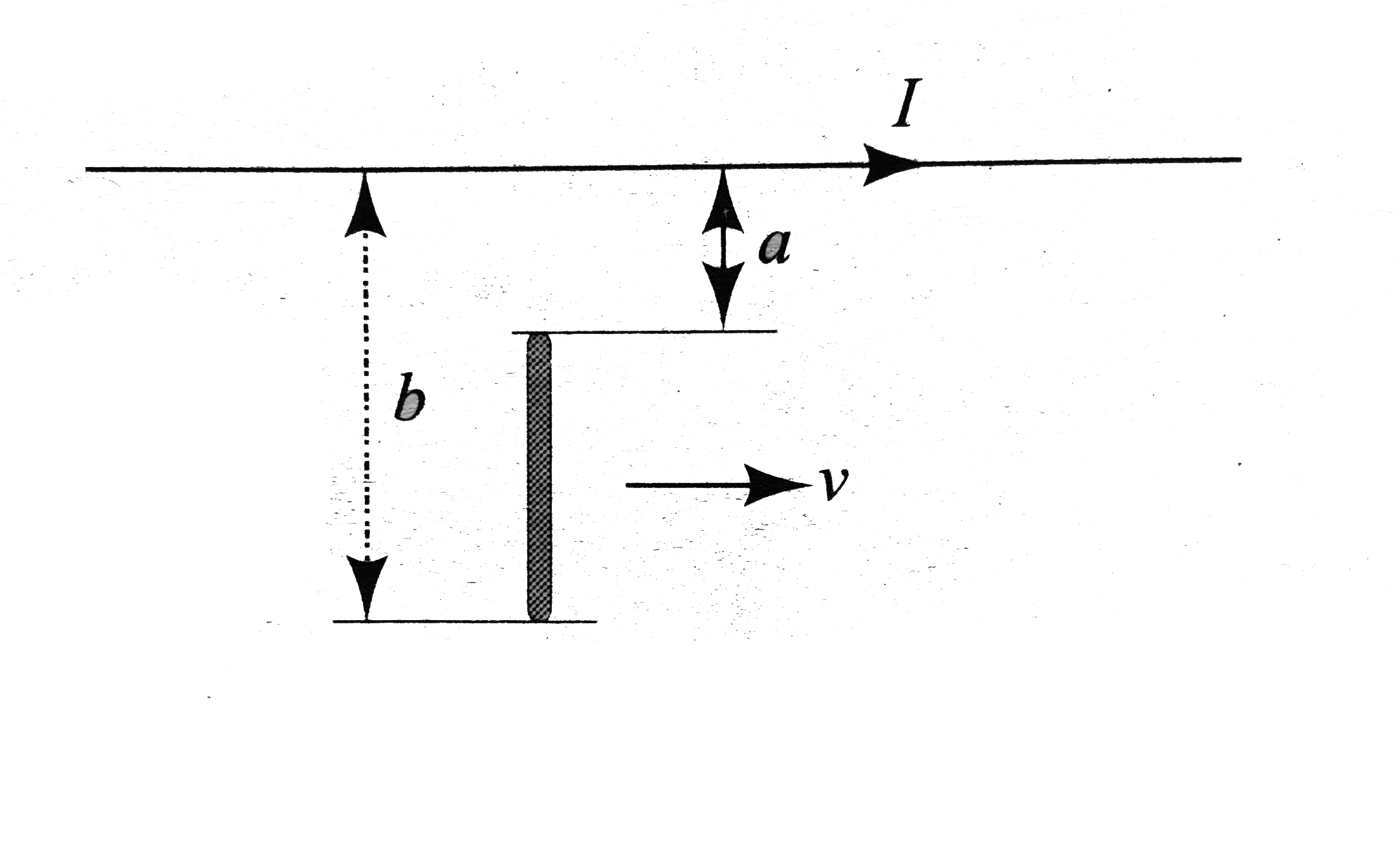 A(a) 0.23mVB(b) 0.46mVC( c) 0.16mVD(d) 0.32mV
A(a) 0.23mVB(b) 0.46mVC( c) 0.16mVD(d) 0.32mV
A rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA copper rod of length 0.19m is moving with uniform velocity 10ms−1 parallel to a long straight wire carrying a current of 5.0A. The rod is perpendicular to the wire with its ends at distances 0.01 and 0.2m from it. Calculate the emf induced in the rod.
View SolutionIn the figure shown AB is a plastic rod moving with a constant velocity v, W is an infinite long wire carrying current I. The end of the rod which is at higher potential is

View SolutionA uniform metal rod is moving with a uniform velocity v parallel to a long straight wire carrying a current I. The rod is perpendicular to the wire with its ends at distance r1andr2 (with r2>r1) form it. The E.M.F. induced in the rod at that instant is
View Solution