A uniform metal rod is moving with a uniform velocity v parallel to a long straight wire carrying a current I. The rod is perpendicular to the wire with its ends at distance r1andr2 (with r2>r1) form it. The E.M.F. induced in the rod at that instant is
zero
μ0Iv2πln(r2r1)
μ0Iv2πln(r1r2)
μ0Iv4π(1−r1r2)
The correct Answer is:B
To find the E.M.F. induced in a uniform metal rod moving parallel to a long straight wire carrying a current, we can follow these steps:
Step 1: Understand the setup
We have a uniform metal rod of length L moving with a uniform velocity v parallel to a long straight wire carrying a current I. The rod is perpendicular to the wire, with its ends at distances r1 and r2 from the wire, where r2>r1.
Step 2: Determine the magnetic field due to the wire
The magnetic field B at a distance r from a long straight wire carrying a current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 3: Calculate the change in magnetic flux
As the rod moves, the magnetic flux Φ through the rod changes. The magnetic flux through the rod can be expressed as:
Φ=B⋅A
where A is the area swept by the rod as it moves. The area A can be expressed as:
A=L⋅d
where d is the distance the rod moves in time dt, which is v⋅dt.
Step 4: Express the change in flux
The change in flux dΦ can be expressed as:
dΦ=B⋅dA=B⋅(L⋅v⋅dt)
Substituting for B:
dΦ=μ0I2πr⋅(L⋅v⋅dt)
Step 5: Integrate to find the total change in flux
To find the total change in flux as the rod moves from r1 to r2, we integrate:
Φ=∫r2r1μ0I2πrL⋅vdr
This gives:
Φ=μ0ILv2π∫r2r11rdr=μ0ILv2π(lnr)r2r1
Φ=μ0ILv2π(lnr2−lnr1)=μ0ILv2πln(r2r1)
Step 6: Find the induced E.M.F.
The induced E.M.F. ϵ in the rod is given by Faraday's law of electromagnetic induction:
ϵ=−dΦdt
Since Φ depends on t through the motion of the rod, we differentiate:
ϵ=−ddt(μ0ILv2πln(r2r1))
Since μ0,I,L,v are constants, we have:
ϵ=μ0ILv2π⋅1r2⋅dr2dt−1r1⋅dr1dt
However, since r1 and r2 are fixed distances, we can simplify this to:
ϵ=μ0Iv2πln(r2r1)
Final Result
Thus, the induced E.M.F. in the rod is:
ϵ=μ0Iv2πln(r2r1)
We have a uniform metal rod of length L moving with a uniform velocity v parallel to a long straight wire carrying a current I. The rod is perpendicular to the wire, with its ends at distances r1 and r2 from the wire, where r2>r1.
The magnetic field B at a distance r from a long straight wire carrying a current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
As the rod moves, the magnetic flux Φ through the rod changes. The magnetic flux through the rod can be expressed as:
Φ=B⋅A
where A is the area swept by the rod as it moves. The area A can be expressed as:
A=L⋅d
where d is the distance the rod moves in time dt, which is v⋅dt.
The change in flux dΦ can be expressed as:
dΦ=B⋅dA=B⋅(L⋅v⋅dt)
Substituting for B:
dΦ=μ0I2πr⋅(L⋅v⋅dt)
To find the total change in flux as the rod moves from r1 to r2, we integrate:
Φ=∫r2r1μ0I2πrL⋅vdr
This gives:
Φ=μ0ILv2π∫r2r11rdr=μ0ILv2π(lnr)r2r1
Φ=μ0ILv2π(lnr2−lnr1)=μ0ILv2πln(r2r1)
The induced E.M.F. ϵ in the rod is given by Faraday's law of electromagnetic induction:
ϵ=−dΦdt
Since Φ depends on t through the motion of the rod, we differentiate:
ϵ=−ddt(μ0ILv2πln(r2r1))
Since μ0,I,L,v are constants, we have:
ϵ=μ0ILv2π⋅1r2⋅dr2dt−1r1⋅dr1dt
However, since r1 and r2 are fixed distances, we can simplify this to:
ϵ=μ0Iv2πln(r2r1)
Thus, the induced E.M.F. in the rod is:
ϵ=μ0Iv2πln(r2r1)
Topper's Solved these Questions
Similar Questions
A copper rod of length 0.19m is moving with uniform velocity 10ms−1 parallel to a long straight wire carrying a current of 5.0A. The rod is perpendicular to the wire with its ends at distances 0.01 and 0.2m from it. Calculate the emf induced in the rod.
View SolutionA copper rod of length L is moving at a uniform speed v parallel to along straight wire carrying a current of I as shown in figure-5.25. The rod is perpendicular to the wire with its ends at distance a and b from if . Calculate the motional EMF induced in the rod.
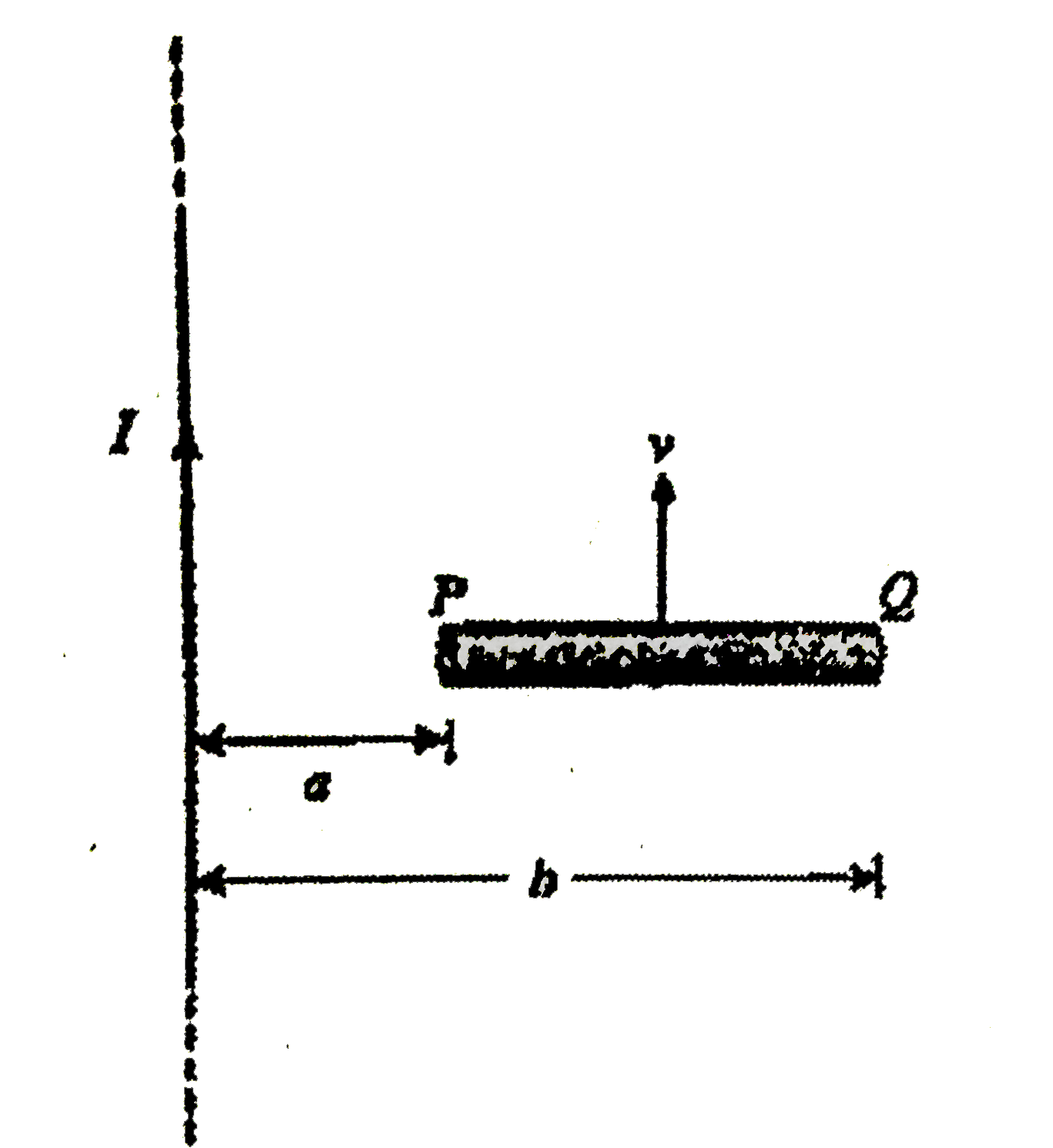
View Solution
Knowledge Check
A copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
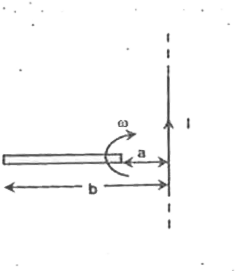 Aμ0i(wa)2πIn(ba)Bμ0i(wb)2πIn(ba)CzeroDμ0iw(a+b)4πIn(ba)
Aμ0i(wa)2πIn(ba)Bμ0i(wb)2πIn(ba)CzeroDμ0iw(a+b)4πIn(ba)Shows a copper rod moving with velocity v parallel to a long straight wire carrying current =100A. Calculate the induced emf in the rod, where v=5mS−1, a=1cm , b=100cm.
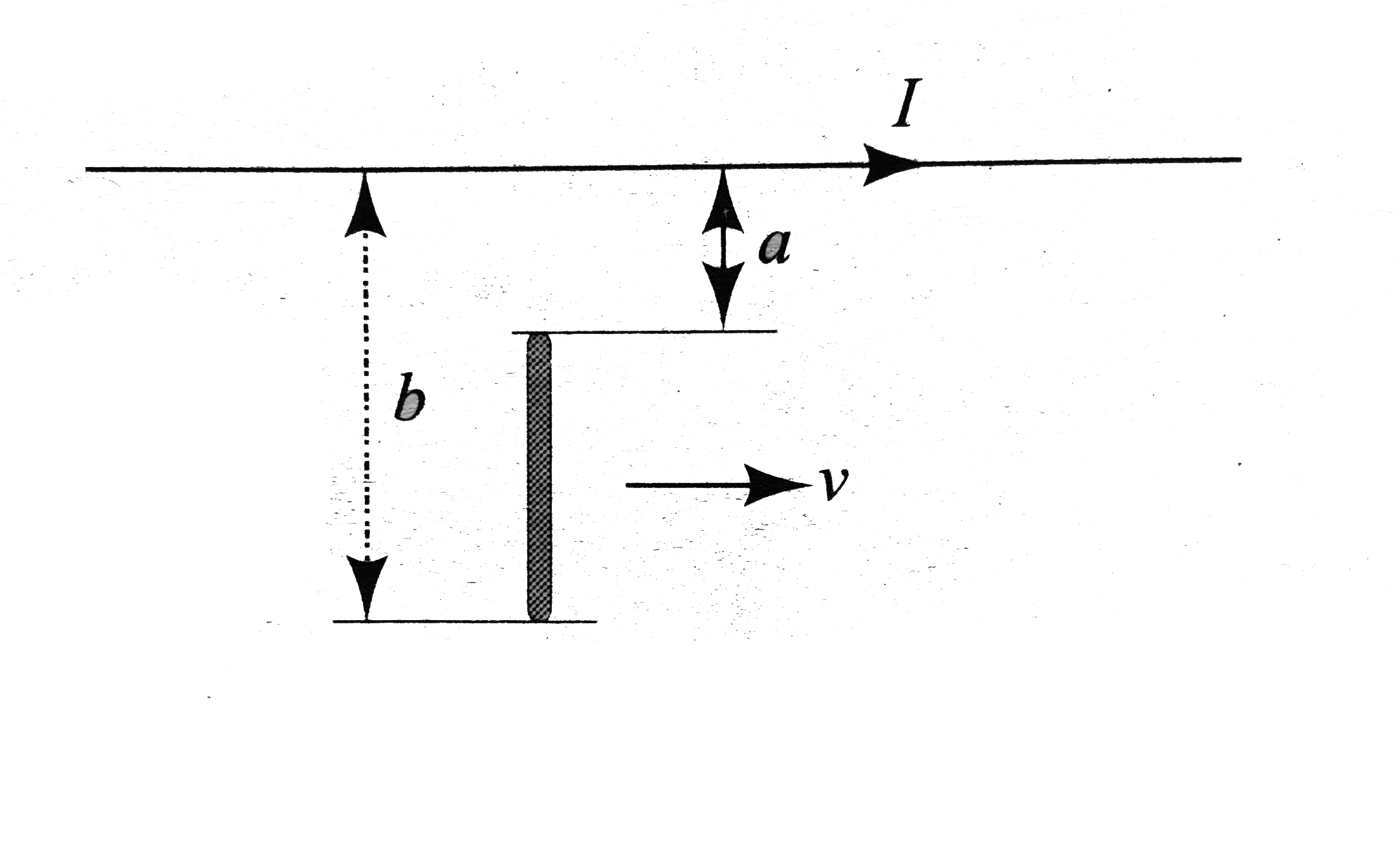 A(a) 0.23mVB(b) 0.46mVC( c) 0.16mVD(d) 0.32mV
A(a) 0.23mVB(b) 0.46mVC( c) 0.16mVD(d) 0.32mVA cionducing rod moves with constant velocity v perpendicular to the straight wire carrying a current I as shown compute that the emf generated between the ends of the rod
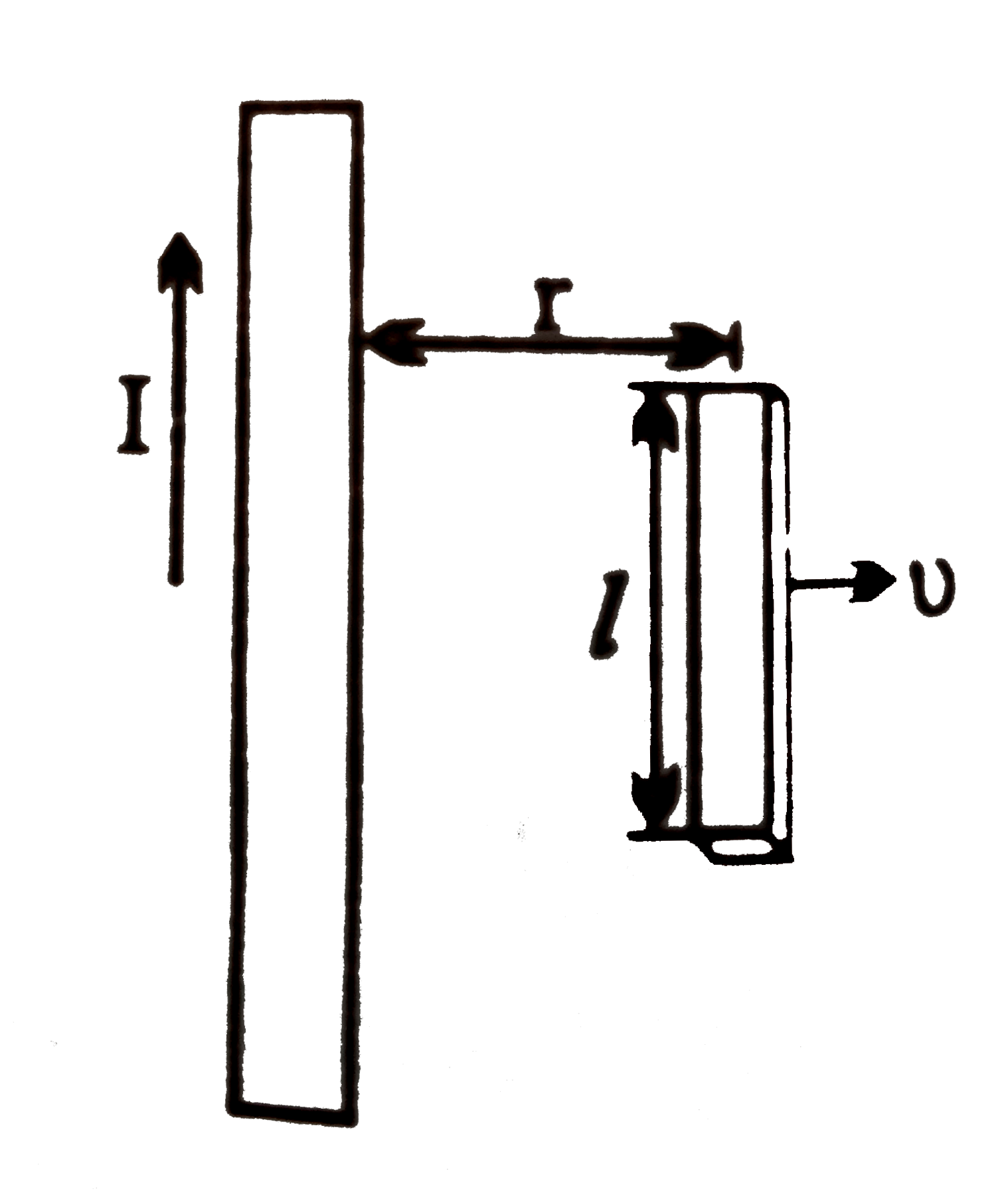 Aμ0vIlπrBμ0vIl2πrC2μ0vIlπrDμ0vIl4πr
Aμ0vIlπrBμ0vIl2πrC2μ0vIlπrDμ0vIl4πr
A conducting rod length 1m moves with a speed of 2m/s parallel to a straight long wire carrying 4A current. Axis of rod is kept perpendicular to the wire with its near end at a distance of 1m from the wire. Magnitude of induced emf in rod is N×10−7log16volt. Find the value of N.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
View SolutionIn the figure shown AB is a plastic rod moving with a constant velocity v, W is an infinite long wire carrying current I. The end of the rod which is at higher potential is

View SolutionThe magnetic flux denisty B at a distance r from a long stright rod carrying a steady current varies with r as show in the
View Solution