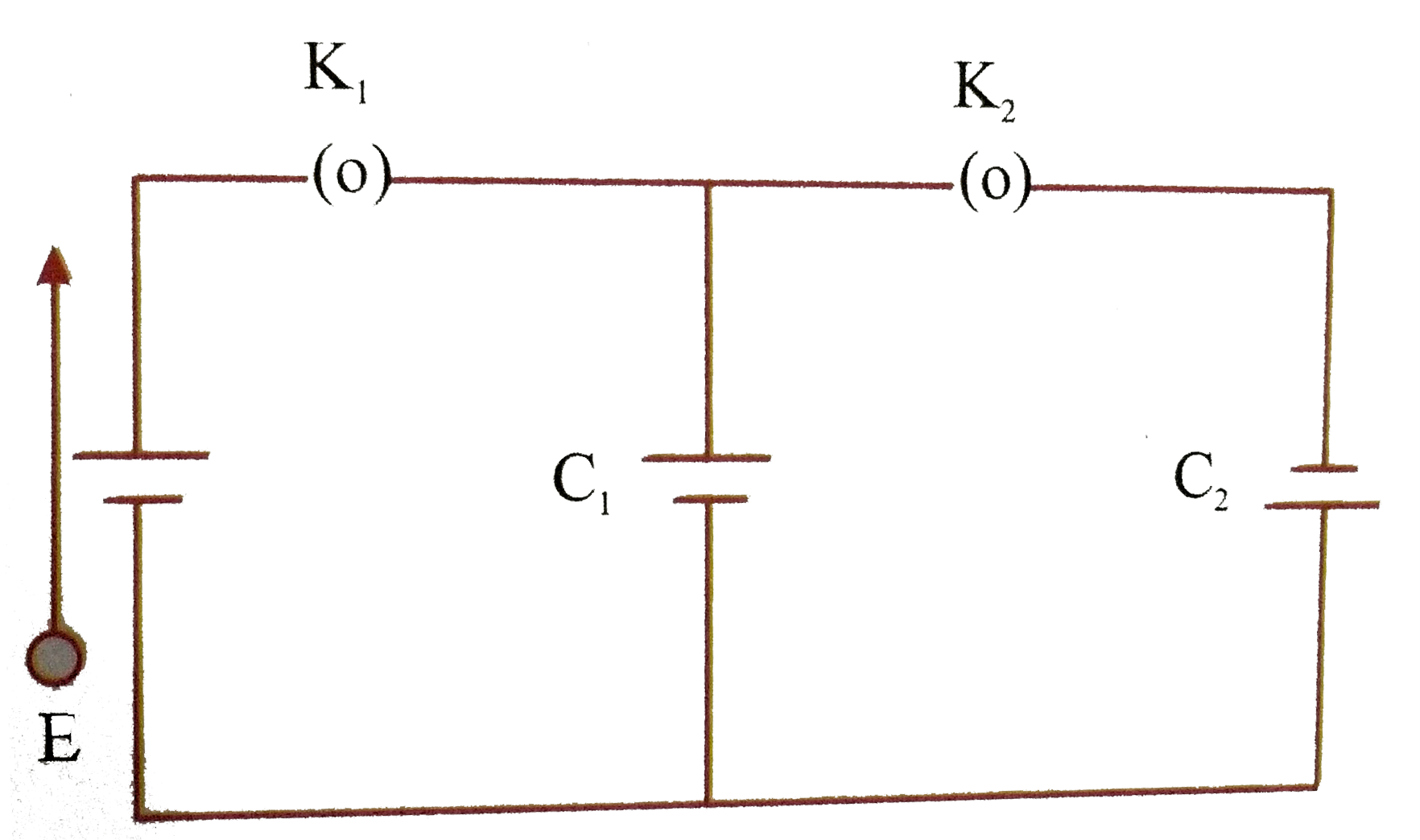
Shown in the figure is a parallel R , L,C circuit with key K1 closed and K2 opened . When K1 is opened and K2 is closed simultaneously find the maximum potential difference across the capacitor and maximum charge stored in it .
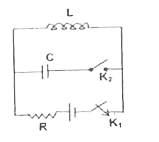
The current flowing through the inductor L in steady state before closing the switch K2 is given as
i=ER(∵ the inductor offers no resistance at steady state ).
The maximum energy stored in the inductor
UL=12Li2=L2(E2)2=LE22R2
Since the maximum energy Uc stored in the capacitor after closing the switch K2 is equal to UL according to conservation of total energy.
Uc=12CV2=UL
⇒12CV2=LE22R2
⇒V=ER√LC ,where V = maximum potential difference across the capacitor
(Maximum charged stored in the capacitor )
qmax=CV=E√LCR
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:SOLVED PROBLEMS ( OBJECTIVE)
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:Comprehension Based Type Comprehension -I
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 9 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTION AND AC CURRENTExercise:Example
Explore 15 Videos
Similar Questions
In the circuit shown in Figure, initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed. Then
View SolutionA circuit containing capacitors C1 and C2 shown in the figure is in the steady state with key K1 cloesed. At the instant t=0 , K1 is opened and K2 is closed.
(a) Find the angular frequency of oscillation of the LC circuit.
(b) Determine the first instant t , when enregy in the indctor becomes one third of that in the capacitor.
(c) Calculate the change on the plates of the capacitor at that instant.
View Solution
Knowledge Check
Shown in the figure is an R−L circuit. Just after the key (K) is closed
 Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuitIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
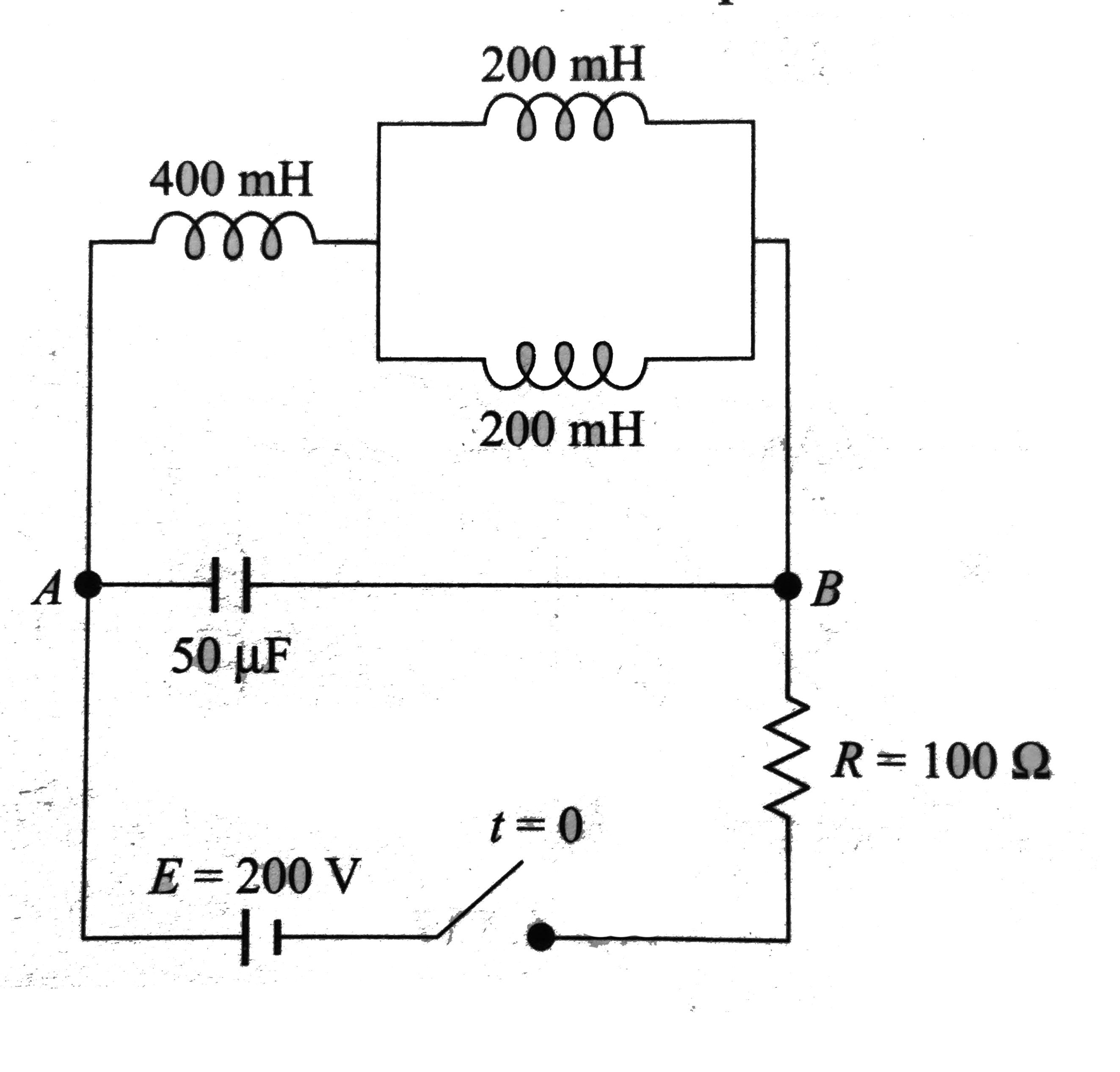
Find the maximum potentail difference across the plates of the capacitor after the switch is opened.A100VB200VC300VD400VIn the circuit shown in fig, switch S was closed for long time. At time t-0, teh switch is opened again. The maximum potential difference across teh plates of the capacitor after the switch is opened is
 A10VB100VC20VD200V
A10VB100VC20VD200V
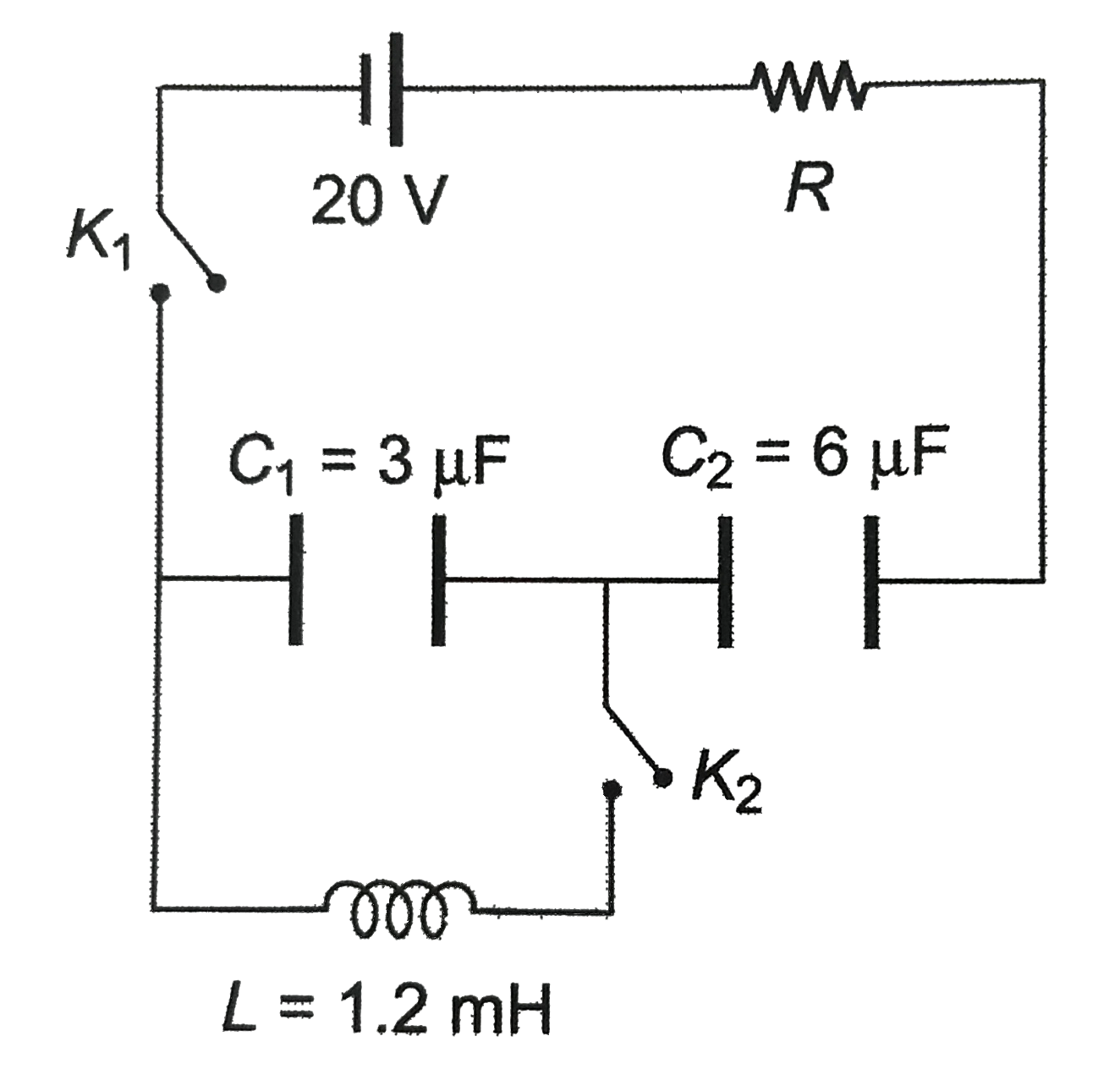
A circuit containing capacitors C1 and C2, shown in the figure is in the steady state with key K1 and K2 opened. At the instant t=0, K1 is opened and K2 is closed.
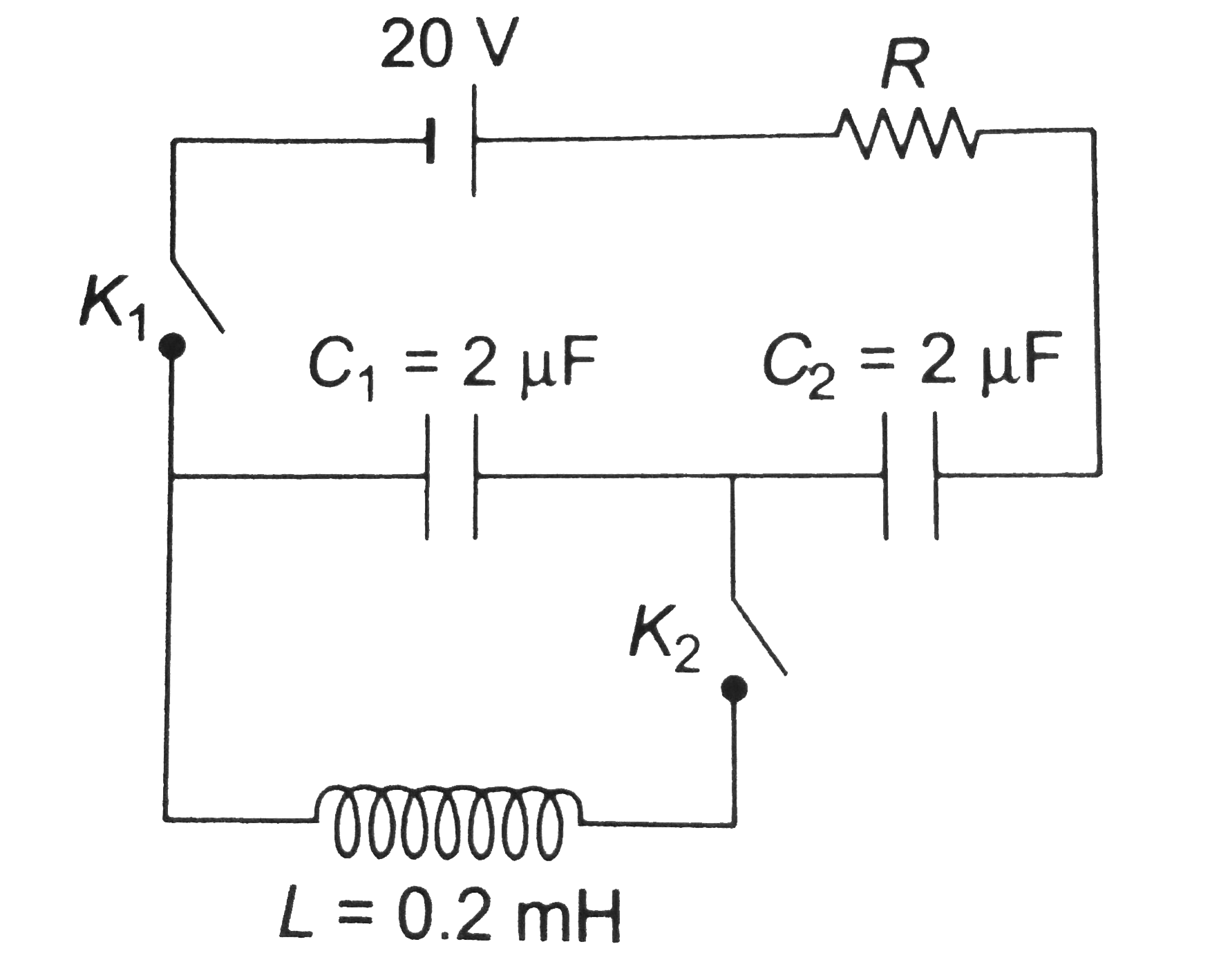
(a) Find the angular frequency of oscillations of L−C circuit.
(b) Determine the first instant t, when energy in the inductor becomes one third of that in the capacitor.
(c) Calculate the charge on the plates of the capacitor at that instant.
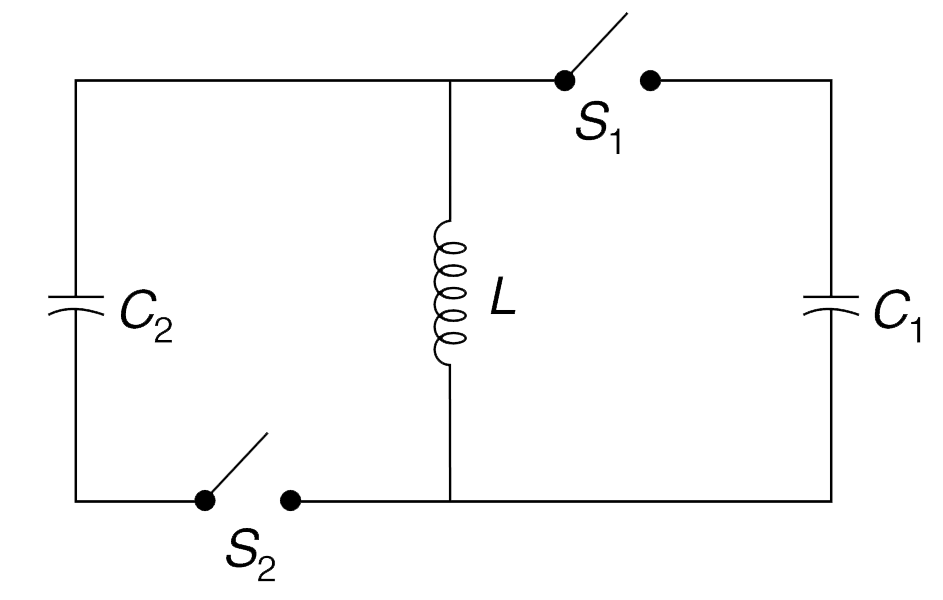
View SolutionThe circuit shown in the figure is used to transfer energy from one capacitor to another. Initially capacitor of capacitance C1=C0 is charged to a potential difference of V0. Switch S1 is closed at time t = 0. After some time S1 is opened and S2 is closed simultaneously. At time t=T,S2 was opened and it was found that the potential difference across capacitor of capacitance C2=C09 was 3V0. Find the smallest possible value of time T. The coil has inductance L. Assume no resistance.
View SolutionIn the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.

View SolutionThe reading of an ammeter in the circuit
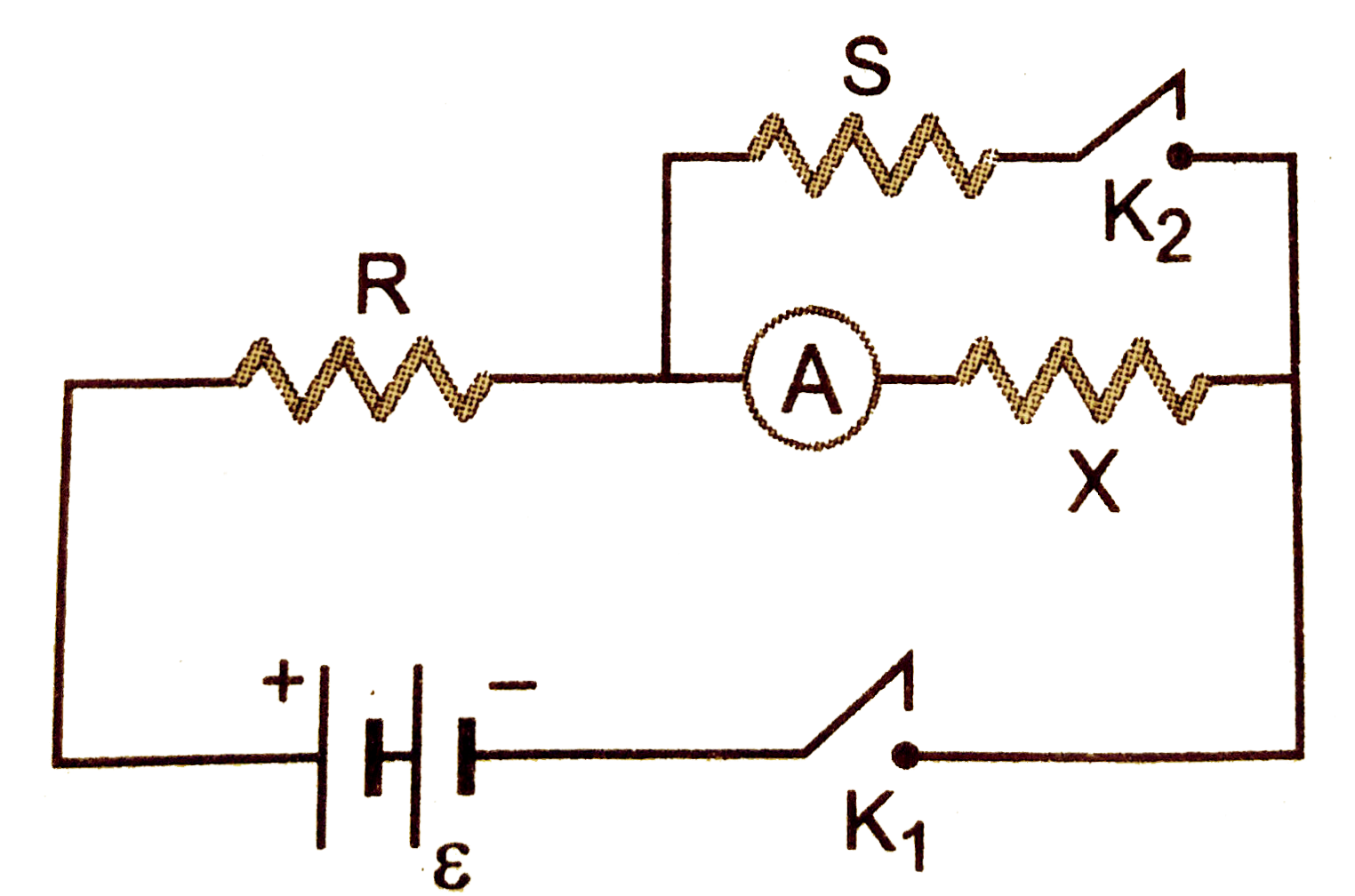
(i) I when key K1 closed key K2 is open
(ii) I/2 when both keys K1andK2 are closed Find the expression for the resistance of X in terms of the resistances of R and S
View SolutionIn the circuit shown in figure , initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q′1 and Q′2 as charges on C1 and C2 and V1 and V2 as voltage respectively].
Then
View Solution

