Two infinite parallel wire, having the cross sectional area 'a' and resistivity 'k' are connected at a junction point 'p' (as shown in the figure). A slide wire of negligible resistance and having mass 'm' and length 'l' can slide between the parallel wires, without any frictional resistance. If the system of wires is introduced to a magnetic field of intensity 'B' (into the plane of paper) and the slide wire is pulled with a force which varies with the velocity of the slide wire as F=F0v, then find the velocity of the slide wire as a function of the distance travelled.
(The slide wire is initially at origin and has a velocity v0)

At any given instance of time the slide wire is at distance x from origin then the resistance of the circuit is R =k(2x+l)a
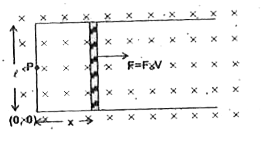
If the velocity of slide wire is V then the emf generated is BlV so we have
BlV−ka(2x+l)l=0
Or, I=Blak(V2x+l)
This current exerts magnetic force in the wire given by F
So F = IlB=Blak(V2x+l)lB=B2l2ak(V2x+l)
Since F−F=mdVdt
So F0V−B2l2ak(V2x+l)=mVdVdx
F0m−B2l2akm(12x+l)=dVdx
∫x0[F0m−B2l2akm(12x+l)]dx=∫vv0dV
F0mx−B2l2a2km{In2x+ll}+v0=V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:SOLVED PROBLEMS ( OBJECTIVE)
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:Comprehension Based Type Comprehension -I
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 9 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTION AND AC CURRENTExercise:Example
Explore 15 Videos
Similar Questions
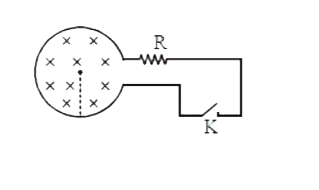
Shown in the figure is a circular loop of radius r and resistance R. A variable magnetic field of induction B=B0e−t is established inside the coil. If the key (K) is closed, the electric power developed right after closing the switch is equal to:-
View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
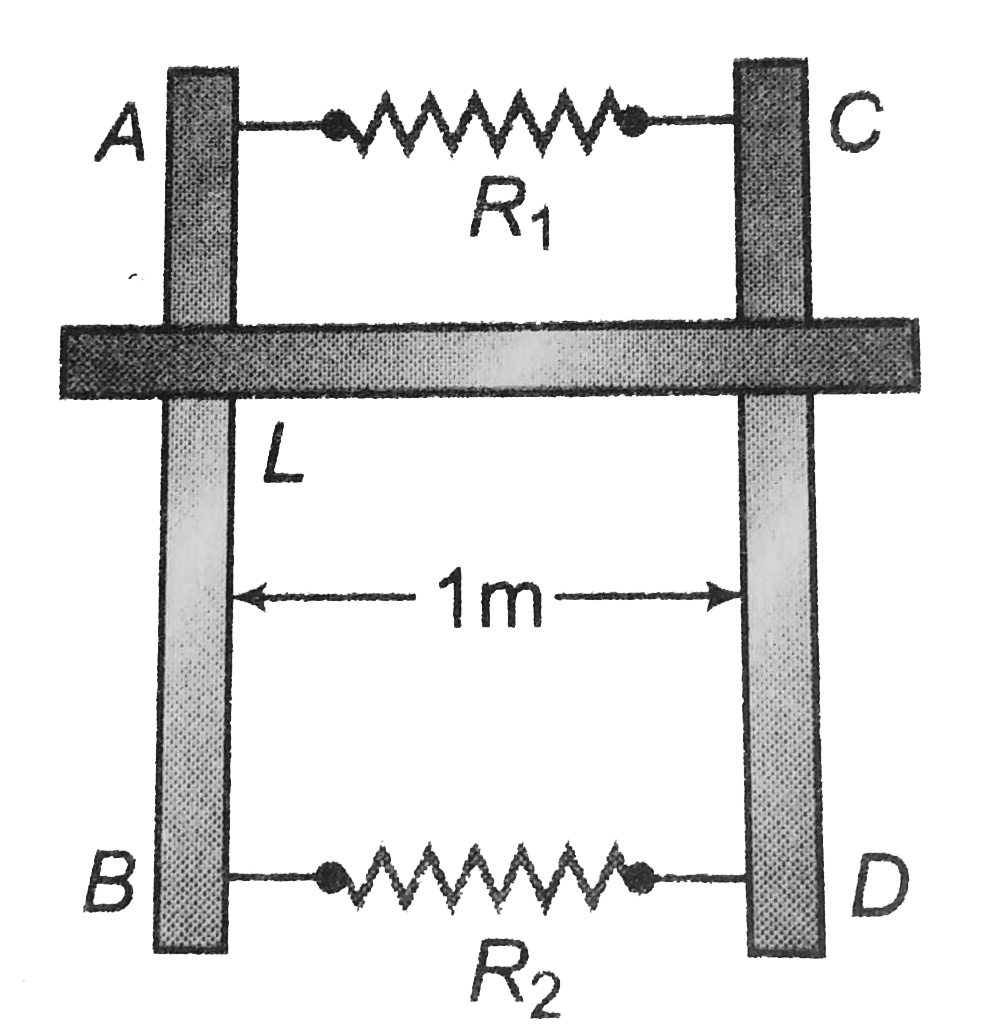
The terminal velocity fo the bar L will be
View SolutionReferring to the previous illustration what will be the induced e.m.f at any instant if the loop is rotated an axis passing through the centre and parallel to the length ?
View SolutionWhen does an elastic metal rod change its length?
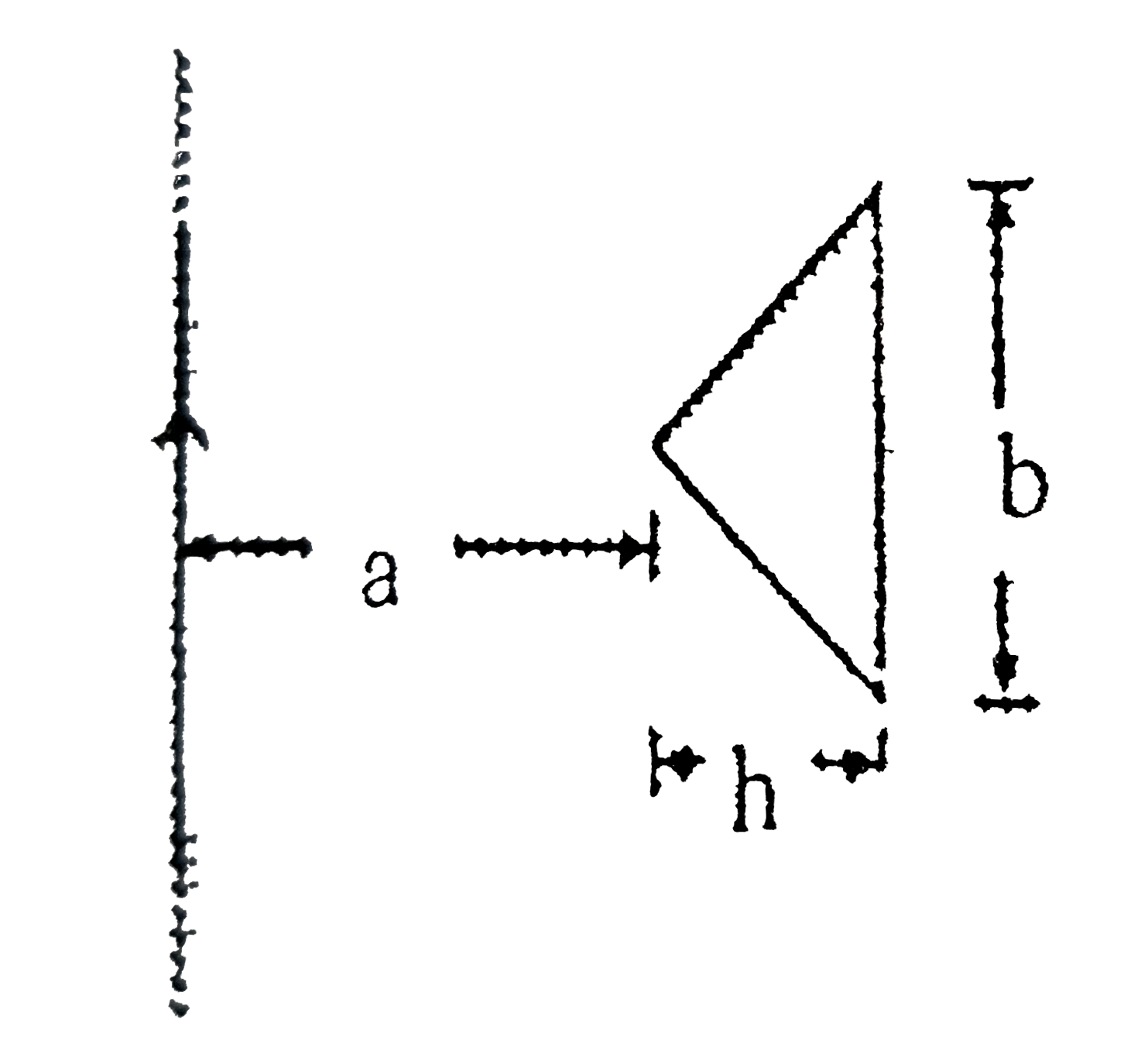
View SolutionA very long staright conductor and an isoceles triangular conductor lie in a plane and separated from each other as shown in the figure.
Given a=10cm, b=20cm and h=10cm
(a) Find their coefficeint of mutual induction.
(b) If current in the staright wire is increasing at a rate of 2A/s , find the direction and magnitude of current in the triangular wire. [Diameter of the wire crosss-section d=1mm, resistivity of the wire, ρ=1.8×10−8Ω−m]
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C . The whole system lies in amagnetic field B and a constant force F is applied to the rod . Then
View SolutionTwo infinite parallel wire, having the cross sectional area 'a' and resistivity 'k' are connected at a junction point 'p' (as shown in the figure). A slide wire of negligible resistance and having mass 'm' and length 'l' can slide between the parallel wires, without any frictional resistance. If the system of wires is introduced to a magnetic field of intensity 'B' (into the plane of paper) and the slide wire is pulled with a force which varies with the velocity of the slide wire as F=F_(0)v , then find the velocity of the slide wire as a function of the distance travelled. (The slide wire is initially at origin and has a velocity v_(0) )
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C . Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View SolutionTwo metallic wires A and B are connected in parallel. Wire A has length l and radius r, wire B has a length 2 l and radius 2r. Compute the ratio of the total resistance of parallel combination and the resistance of wire A.
View SolutionA long straight wire carries a current I0, at distance a and b=3a from it there are two other wires, parallel to the former one, which are interconnected by a resistance R(figure).A connector slides without friction along the wires with a constant velocity v.Assuming the resistance of the wires,the connector, the sliding contacts and the self-inductance of the frame to be negligible. The point of application (distance from the long wire) of magnetic force on sliding wire due to the long wire is 2alnx from long wire.Then find out value of x.

View SolutionA long straight wire carries a current I0. At distance a and b =3a from it there are two other wires, parallel to the former one, which are interconnected by a resistance R ( figure ). A connector slides without friction along the wire with a constant velocity v. Assuming the resistance of the wire, the connector, the sliding contact, and the self-inductance of the frame to be negligible ,
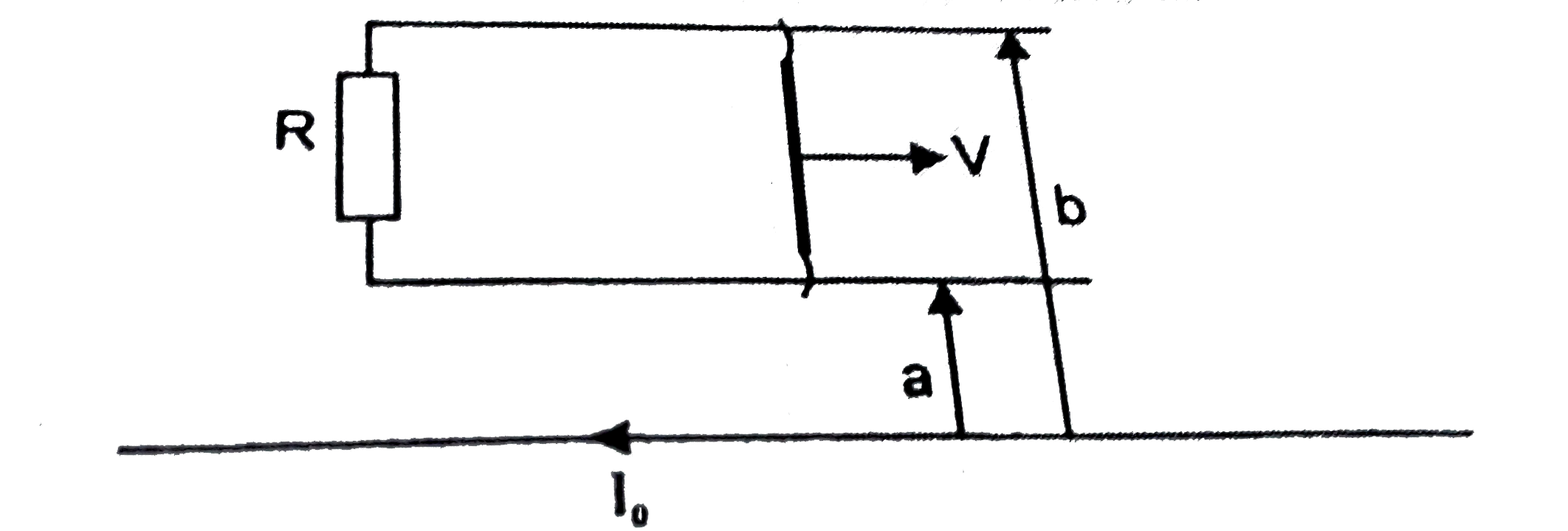
The point of application (distance from the long wire ) of magnetic force on sliding wire due to the long wire is 2alnx from long wire. Then findout value of x.
View SolutionTwo copper wires A and B of length l and 2l respectively, have the same area of cross-section. The ratio of the resistivity of wire A to the resistivity of wire B is
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionA battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
View Solution

