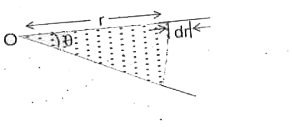
A metallic rod of mass m length R is pivoted at O. It is free to rotate about a horizontal axis passing through O . An inward magnetic field is applied as shown in the figure. Find the ratio of maximum electric field inside the metallic rod to the applied magnetic field induction .

The induced emf between O and P
ε=−dϕdt=−d(BA)dt=−BdAdt
ε=−Bddt[r22θ]=−Br2ω2(∵ω=dθdt)
The potential gradient dεdr=(−Br2ω2)ddr(r2)=−Bωr
⇒ The corresponding electric field E = Bωr
⇒Emax=Bω R where ω = maximum angular speed of the rod that is possible when it becomes vertical . Conservation of meachanical energy between horizontal and vertical yield ,
ΔPEgr+ΔKEr=0
−mgR2+12I0ω2=0
⇒ω=√3gRR
⇒EmaxB=√3gR
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SOLVED PROBLEMS ( OBJECTIVE)
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Comprehension Based Type Comprehension -I
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II
15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTION AND AC CURRENTEXERCISE - Example
15 Videos
Similar Questions
Knowledge Check
A metal rod of length l pivoted at is upper end. It is released from a horizontal position. There is a uniform magnetic field ⊥ to its plane of rotation. When it becomes vertical, the p.d. across its ends is proportional to
Al1/2BlCl3/2Dl2A straight rod of length l si rotating about axis passing through O is shown. A uniform magnetic field B exists parallel to the axis of rotation. E.m.f induced between P and Q is:
 A825Bωl2B310Bωl2C725BωlDzero
A825Bωl2B310Bωl2C725BωlDzero
Find the magnetic field at the centre O of the loop shown in the figure
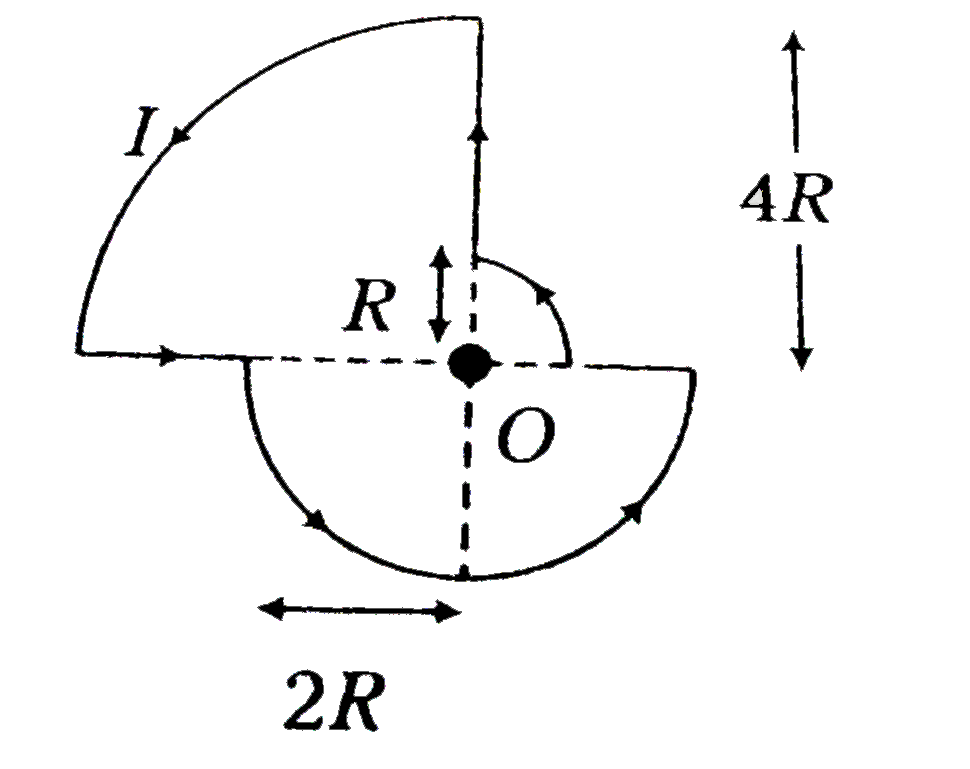
View SolutionA thin ring of mass 0.1kg and diameter 0.5m carrying charge q is free to rotate about an axis as shown in the figure.At t=0, time dependent magnetic field of 8t Tesla is applied vertically down on the ring.If the ring is at rest before applying magnetic field and induced magnetic effects due to rotation of the ring are neglected,the power developed by the force acting on the ring after 10sec is found to be 6.4mw .Find the charge q that the ring is carrying?
View SolutionA rod of length 1m rotates about one of its end points with an angular velocity 2rad/sec in a plane perpendicular to the magnetic field B=2T as shown in the figure. Then find magnitude of electric field (in SI unit) at the mid point of the rod.

View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View Solution


