A ball is projected with velocity v0 at an angle α to the horizonal, towards a smooth wall which appraches the ball. With velocity u. After collision the ball retraces its path to the point of projection . What is the time t taken by the ball form the instant of projection to point of impact ?

Step by step video & image solution for A ball is projected with velocity v_(0) at an angle alpha to the horizonal, towards a smooth wall which appraches the ball. With velocity u. After collision the ball retraces its path to the point of projection . What is the time t taken by the ball form the instant of projection to point of impact ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:Level 1
Explore 110 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:L-2
Explore 21 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- RIGID BODY MOTIONBook:ANURAG MISHRAChapter:RIGID BODY MOTIONExercise:MATCH THE COLUMN
Explore 12 Videos
Similar Questions
A ball is projected with velocity (u) at an anle α with horizontal plane. What is its speed when it makes an angle θ whith the horizontal plane ?
View SolutionA small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
View Solution
Knowledge Check
An inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
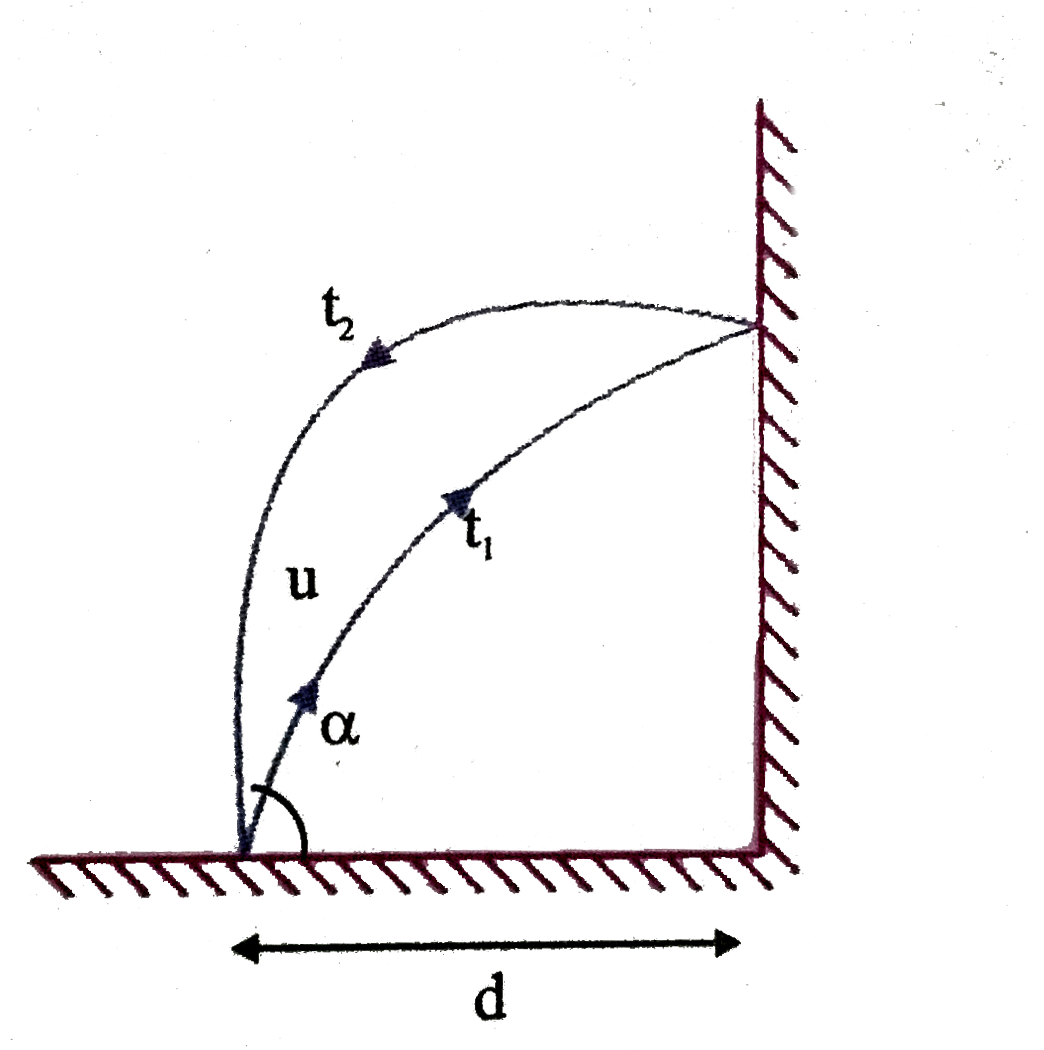
If the line joining the point of projection and the point of impact makes an angle 'θ' with the horizontal, then tanθ isAetanαB(1+e)tanαC(1+e)tanαDtanα(1+e)An inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
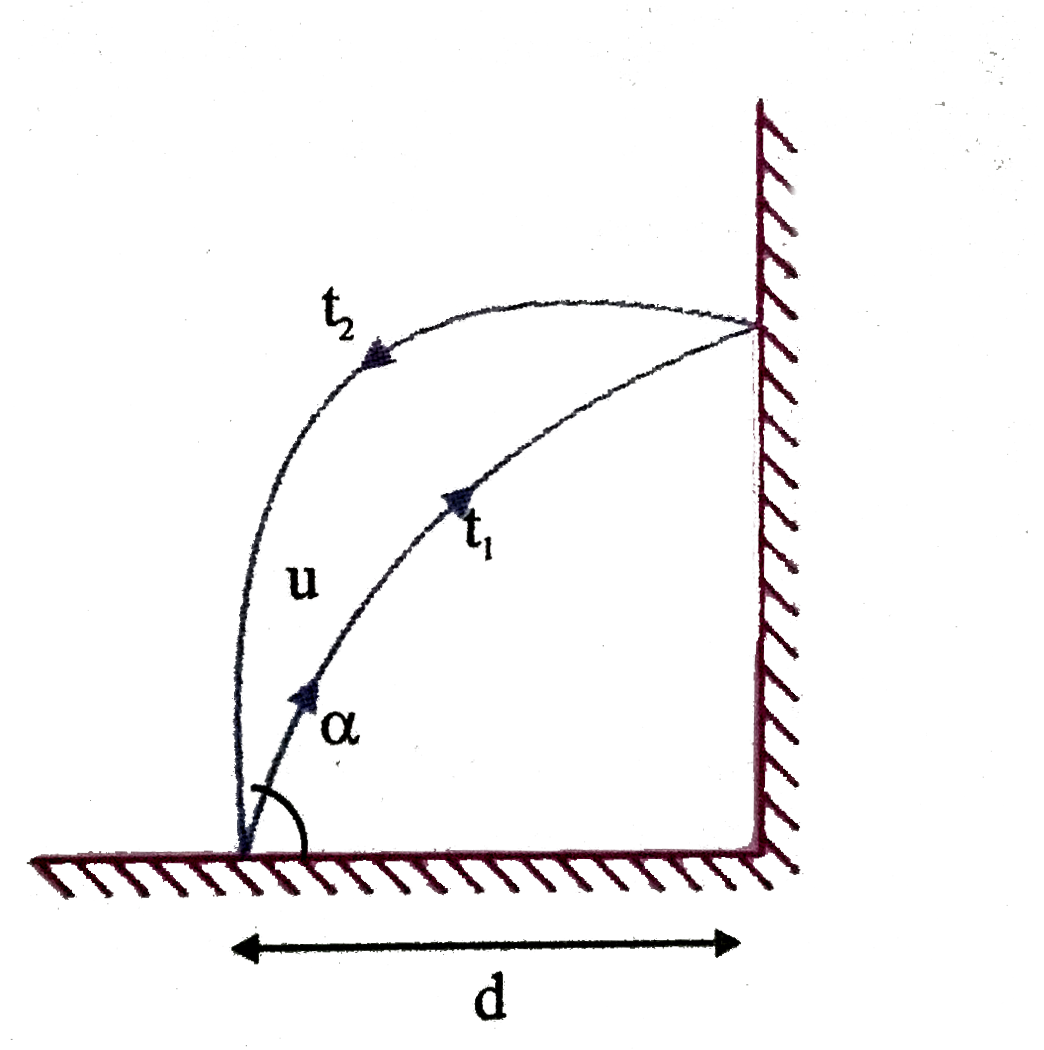
The total time of journey of the ball isAusinαgB2usinαgC2ucosαgDutanα2gAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
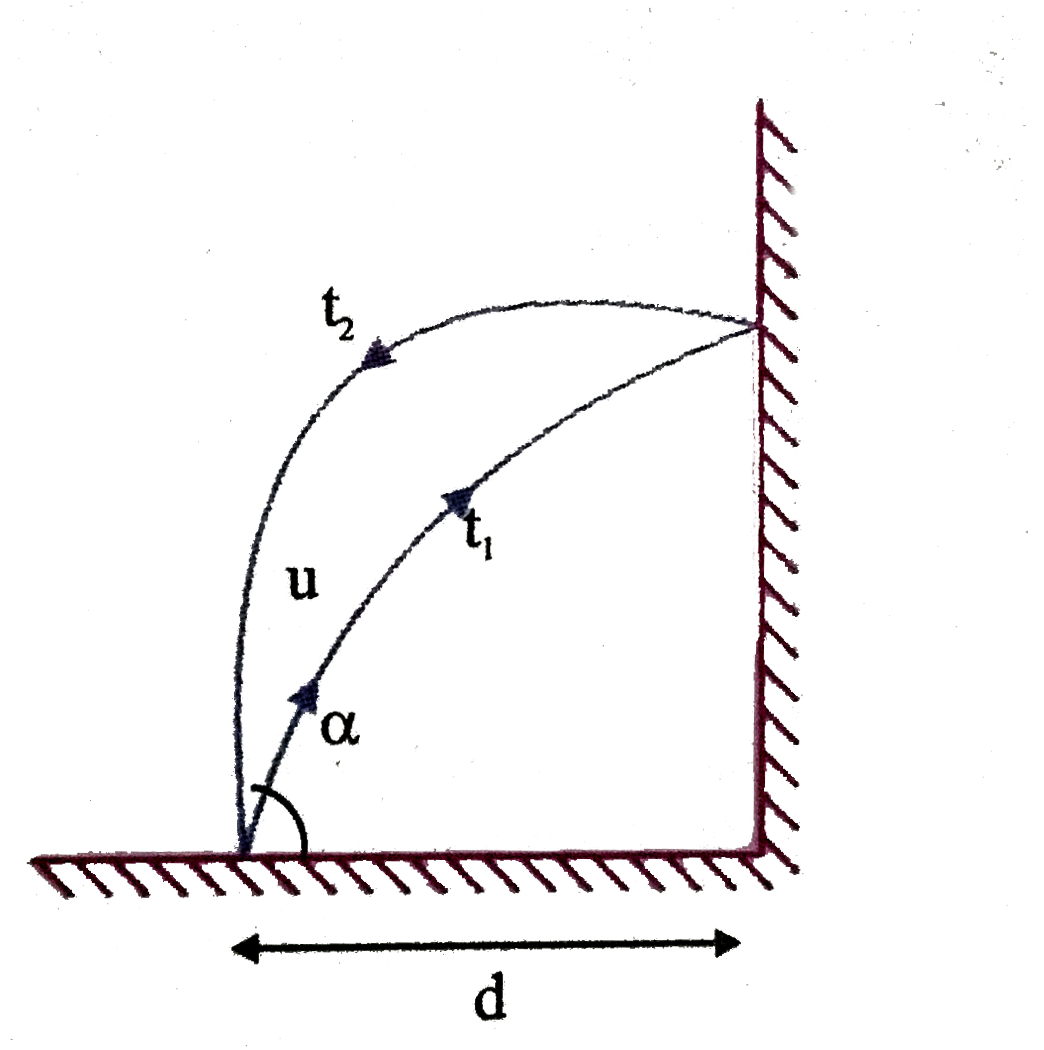
The horizontal distance 'd' from the wall isAu2sin2αg(e1+e)Bu2sinαg(e1+e)Cu2cos2αg(e1+e)Du2sin2α2g(e1+e)
A ball is projected with an velocityV0 at an angle of elevation 30∘. Mark of the correct statement.
View SolutionA small ball thrown at an initial velocity v0 at an angle α to the horizontal strikes elastically with a smooth vertical wall moving towards it at a horizontal velocity v and returns to the point from which it was thrown. Determine the time t from the beginning of motions to the moment of impact with vertical wall. Neglect friction losses.
View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
View SolutionA ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collision with a vertical wall and returns to ground. The total time of flight of the ball is
View SolutionA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :

View Solution

