A small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
To solve the problem of finding the maximum distance d for which a ball projected at an angle returns to the point of projection after rebounding from a smooth vertical wall, we can follow these steps:
Step 1: Understand the motion of the ball
The ball is projected with an initial velocity u at an angle θ to the horizontal. It will travel towards the wall and rebound off it. The motion can be analyzed in two components: horizontal and vertical.
Step 2: Calculate the time to reach the wall
The horizontal component of the velocity is given by:
ux=ucosθ
The time taken to reach the wall, which is at a distance d, is:
t1=ducosθ
Step 3: Calculate the vertical motion
The vertical component of the velocity is:
uy=usinθ
Using the equation of motion in the vertical direction, we can find the vertical displacement when the ball reaches the wall:
y=uyt1−12gt21
Substituting t1:
y=usinθ(ducosθ)−12g(ducosθ)2
Simplifying this gives:
y=dtanθ−gd22u2cos2θ
Step 4: Analyze the rebound
Upon rebounding from the wall, the ball will have a new horizontal velocity component, which is affected by the coefficient of restitution e:
vx=eucosθ
The time taken to return to the original position after rebounding is:
t2=dvx=deucosθ
Step 5: Total time of flight
The total time of flight T is the sum of the time to reach the wall and the time to return:
T=t1+t2=ducosθ+deucosθ
Factoring out ducosθ:
T=ducosθ(1+1e)
Step 6: Relate total time to vertical motion
The total time of flight can also be expressed in terms of the vertical motion:
T=2usinθg
Step 7: Equate the two expressions for total time
Setting the two expressions for T equal gives:
ducosθ(1+1e)=2usinθg
Step 8: Solve for d
Rearranging this equation to solve for d:
d=2u2sinθcosθg(1+1e)
Using the identity sin2θ=2sinθcosθ:
d=u2sin2θg(1+1e)
Step 9: Find maximum d
To find the maximum distance d, we need to maximize sin2θ, which has a maximum value of 1. Thus, the maximum distance dmax is:
dmax=u2g(1+1e)
Final Result
The maximum distance d for which the ball may return to the point of projection after rebounding from the wall is:
dmax=eu2g(e+1)
The ball is projected with an initial velocity u at an angle θ to the horizontal. It will travel towards the wall and rebound off it. The motion can be analyzed in two components: horizontal and vertical.
The horizontal component of the velocity is given by:
ux=ucosθ
The time taken to reach the wall, which is at a distance d, is:
t1=ducosθ
The vertical component of the velocity is:
uy=usinθ
Using the equation of motion in the vertical direction, we can find the vertical displacement when the ball reaches the wall:
y=uyt1−12gt21
Substituting t1:
y=usinθ(ducosθ)−12g(ducosθ)2
Simplifying this gives:
y=dtanθ−gd22u2cos2θ
Upon rebounding from the wall, the ball will have a new horizontal velocity component, which is affected by the coefficient of restitution e:
vx=eucosθ
The time taken to return to the original position after rebounding is:
t2=dvx=deucosθ
The total time of flight T is the sum of the time to reach the wall and the time to return:
T=t1+t2=ducosθ+deucosθ
Factoring out ducosθ:
T=ducosθ(1+1e)
The total time of flight can also be expressed in terms of the vertical motion:
T=2usinθg
Setting the two expressions for T equal gives:
ducosθ(1+1e)=2usinθg
Rearranging this equation to solve for d:
d=2u2sinθcosθg(1+1e)
Using the identity sin2θ=2sinθcosθ:
d=u2sin2θg(1+1e)
To find the maximum distance d, we need to maximize sin2θ, which has a maximum value of 1. Thus, the maximum distance dmax is:
dmax=u2g(1+1e)
The maximum distance d for which the ball may return to the point of projection after rebounding from the wall is:
dmax=eu2g(e+1)
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Textbook Exercise)
Explore 23 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Additional Exercise)
Explore 7 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Conceptual Questions
Explore 20 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball projected from the ground with speed 10m/s at an angle of 45∘ with horizontal. It collides with a wall at a distance 2 m from the point of projection and returns to its original position. If the coefficient of restitution between the ball and wall is 1/x, find x.
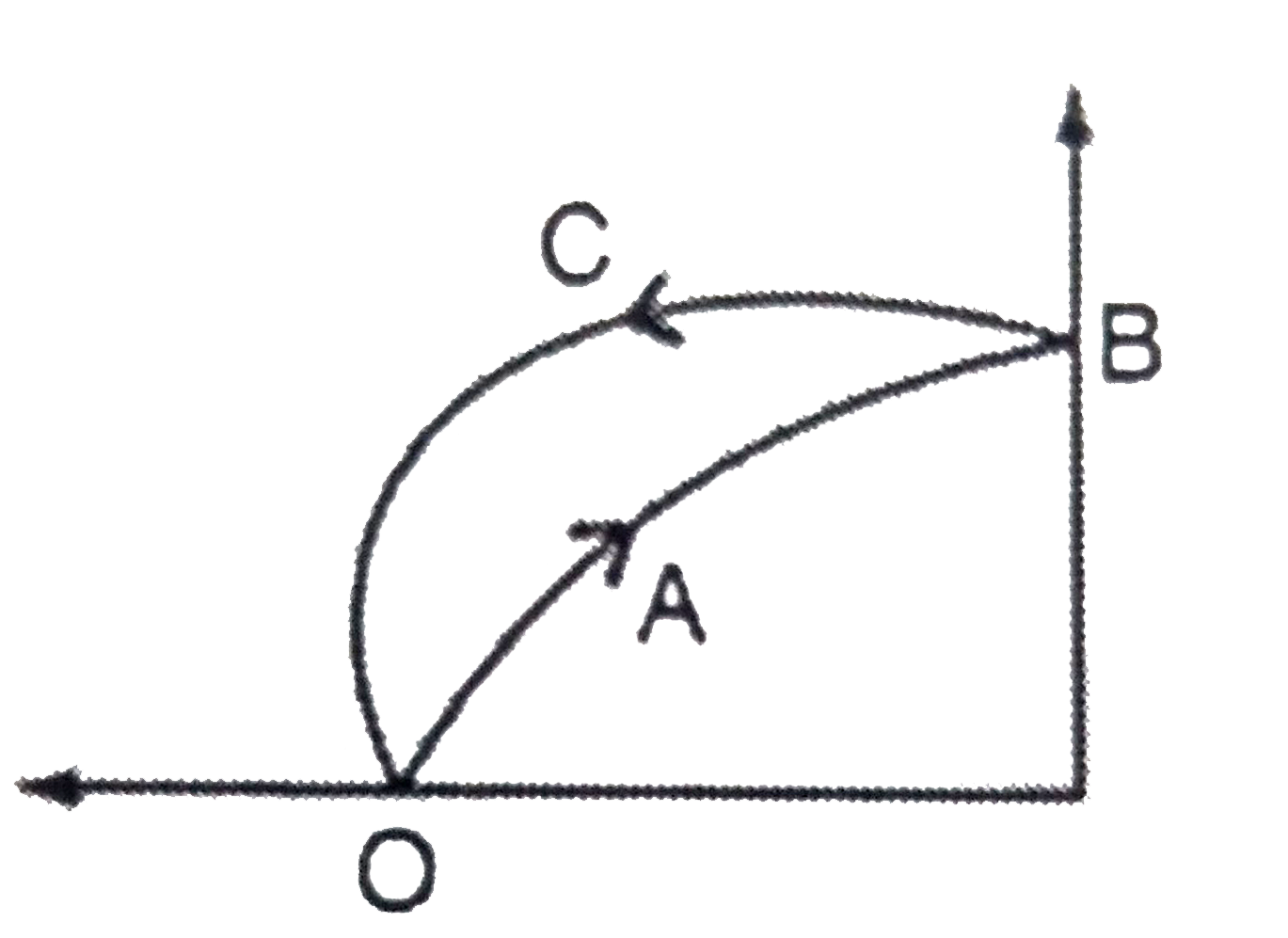
View Solution
Knowledge Check
A ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at t=2v0sinθgBd=e(R−L)(whereRisv0sin2θg)Cmaximum height during motion =v20sin2θ2gDit will return to ground at t<2v0sinθgA projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
Av0Bv0sinαCv0cosαD√gR2An inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
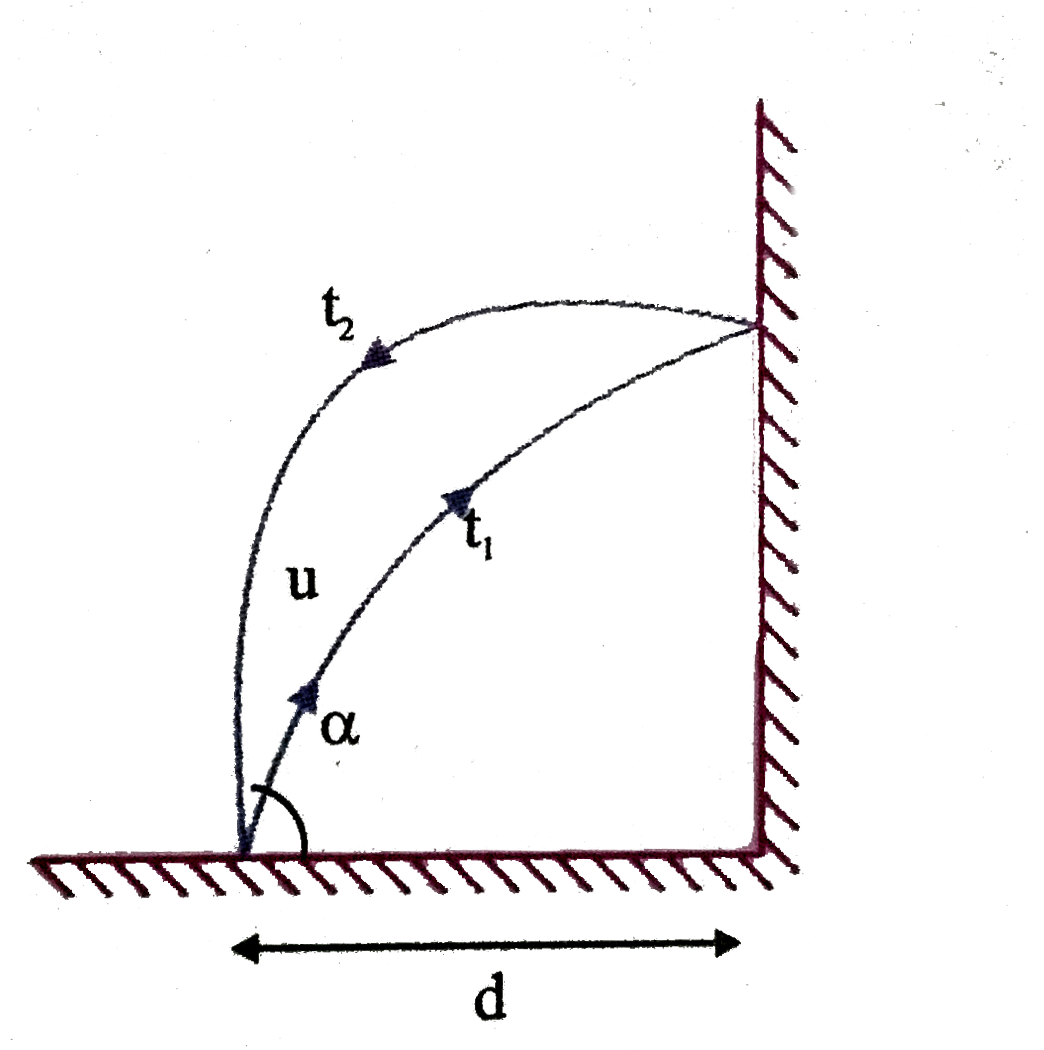
If the line joining the point of projection and the point of impact makes an angle 'θ' with the horizontal, then tanθ isAetanαB(1+e)tanαC(1+e)tanαDtanα(1+e)
A ball is projected from a given point with velocity u at some angle with the horizontal and after hitting a vertical wall returns to the same point. Show that the distance of the point from the wall must be less than eu2(1+e)g, where e is the coefficient of restitution.
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
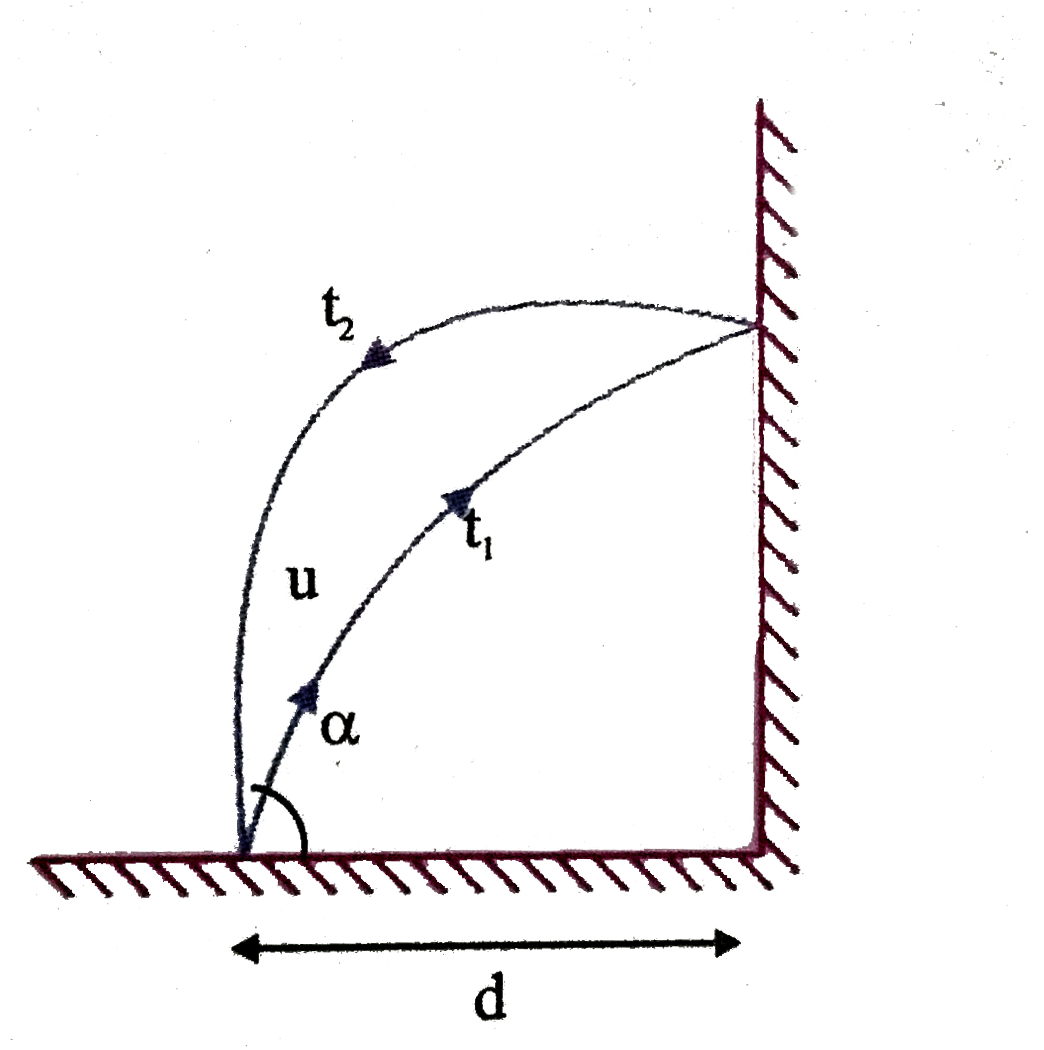
The horizontal distance 'd' from the wall is
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
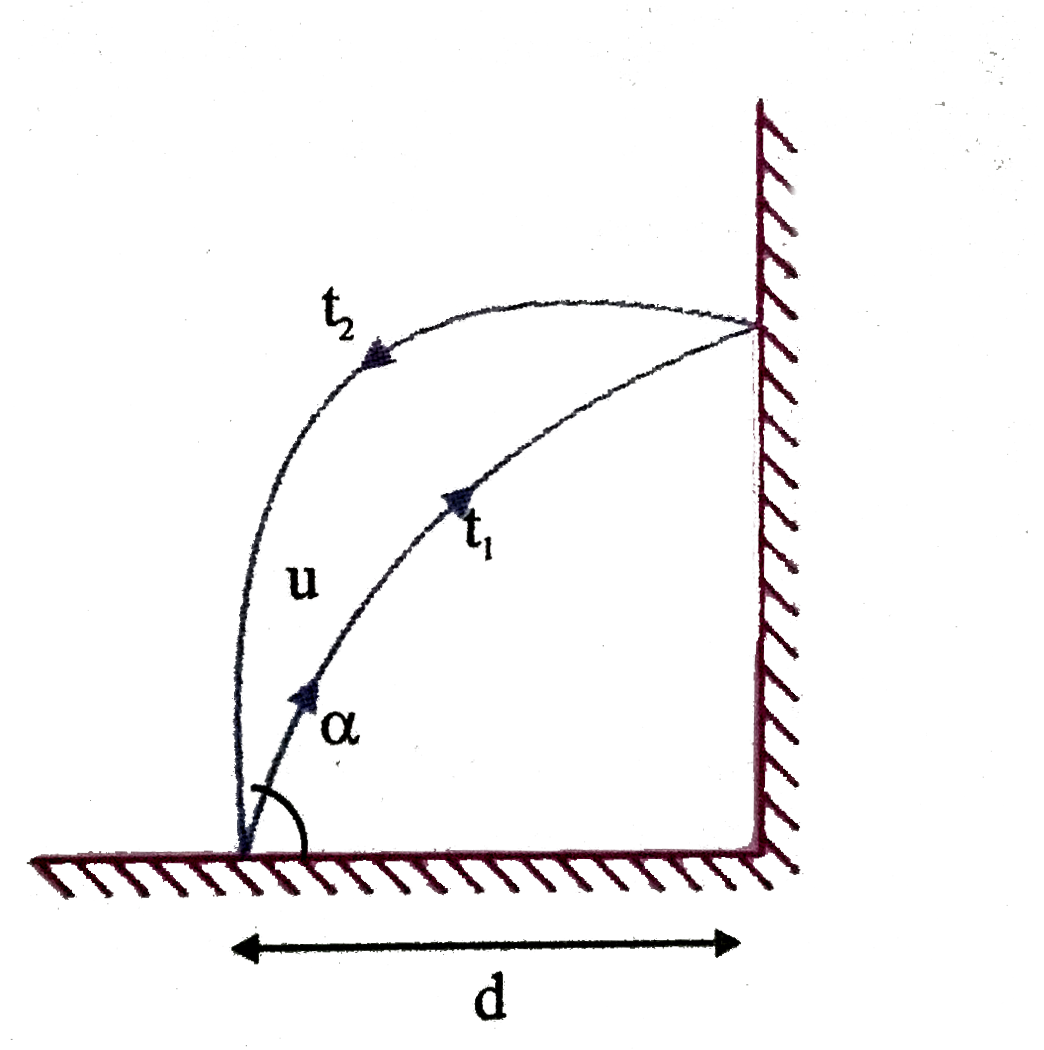
The total time of journey of the ball is
View SolutionA girl throws a ball with an initial velocity v at an angle 45∘. The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebound returns to her hands. What is the coefficient of restitution between wall and ball ? (v2>dg)
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is

View Solution

