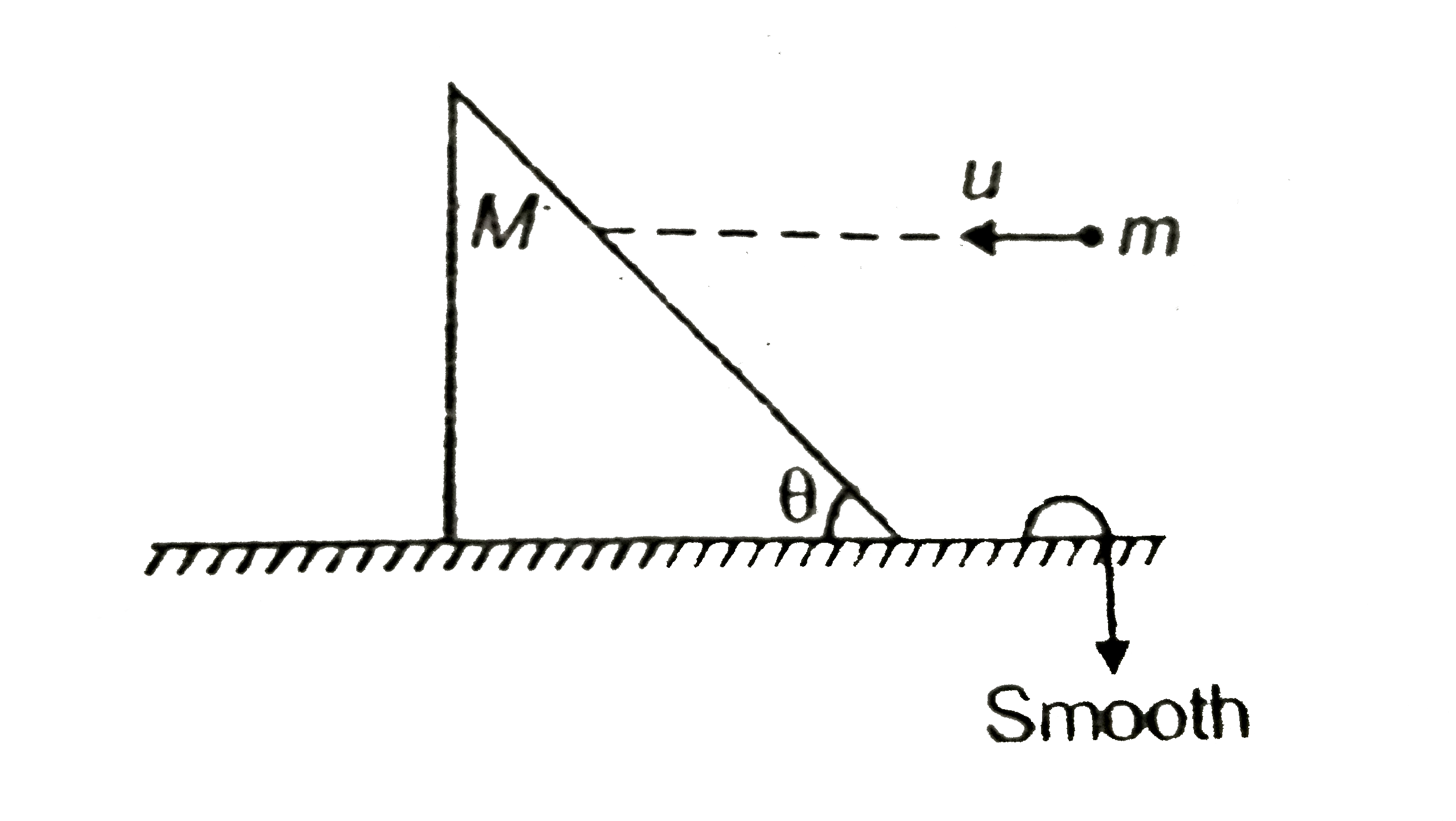
A smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
To solve the problem of finding the velocity of the wedge after the collision, we will follow these steps:
Step 1: Understand the system
We have a wedge of mass M on a smooth horizontal surface, and a particle of mass m colliding with the wedge's inclined face at an angle θ. The initial speed of the particle before the collision is u.
Step 2: Apply conservation of momentum
Since there are no external forces acting on the system in the horizontal direction, we can apply the conservation of momentum. Before the collision, only the particle is moving. After the collision, both the wedge and the particle will be moving.
Let:
- v1 be the velocity of the wedge after the collision.
- v2 be the velocity of the particle after the collision.
The momentum before the collision is:
Initial Momentum=m⋅u
The momentum after the collision is:
Final Momentum=M⋅v1+m⋅v2⋅cos(90∘−θ)
Since cos(90∘−θ)=sin(θ), we can rewrite it as:
M⋅v1+m⋅v2⋅sin(θ)
Setting the initial momentum equal to the final momentum gives us:
m⋅u=M⋅v1+m⋅v2⋅sin(θ)(1)
Step 3: Use the coefficient of restitution
The coefficient of restitution e relates the relative velocities of separation and approach. The formula is:
e=Velocity of separationVelocity of approach
The velocity of approach is u (the speed of the particle before collision). The velocity of separation can be expressed as:
Velocity of separation=v1⋅sin(θ)−v2
Substituting into the equation for e:
e=v1⋅sin(θ)−v2u(2)
Step 4: Solve for v2
From equation (2), we can rearrange to find v2:
v2=v1⋅sin(θ)−e⋅u(3)
Step 5: Substitute v2 back into the momentum equation
Now, substitute equation (3) into equation (1):
m⋅u=M⋅v1+m⋅(v1⋅sin(θ)−e⋅u)⋅sin(θ)
Expanding this gives:
m⋅u=M⋅v1+m⋅v1⋅sin2(θ)−m⋅e⋅u⋅sin(θ)
Step 6: Rearranging the equation
Rearranging the equation to isolate v1:
m⋅u+m⋅e⋅u⋅sin(θ)=M⋅v1+m⋅v1⋅sin2(θ)
Factoring out v1:
m⋅u(1+e⋅sin(θ))=v1(M+m⋅sin2(θ))
Step 7: Solve for v1
Finally, solving for v1:
v1=m⋅u(1+e⋅sin(θ))M+m⋅sin2(θ)
Final Answer
The velocity of the wedge after the collision is:
v1=m⋅u(1+e⋅sin(θ))M+m⋅sin2(θ)
We have a wedge of mass M on a smooth horizontal surface, and a particle of mass m colliding with the wedge's inclined face at an angle θ. The initial speed of the particle before the collision is u.
Since there are no external forces acting on the system in the horizontal direction, we can apply the conservation of momentum. Before the collision, only the particle is moving. After the collision, both the wedge and the particle will be moving.
- v1 be the velocity of the wedge after the collision.
- v2 be the velocity of the particle after the collision.
Initial Momentum=m⋅u
Final Momentum=M⋅v1+m⋅v2⋅cos(90∘−θ)
Since cos(90∘−θ)=sin(θ), we can rewrite it as:
M⋅v1+m⋅v2⋅sin(θ)
m⋅u=M⋅v1+m⋅v2⋅sin(θ)(1)
The coefficient of restitution e relates the relative velocities of separation and approach. The formula is:
e=Velocity of separationVelocity of approach
Velocity of separation=v1⋅sin(θ)−v2
e=v1⋅sin(θ)−v2u(2)
From equation (2), we can rearrange to find v2:
v2=v1⋅sin(θ)−e⋅u(3)
Now, substitute equation (3) into equation (1):
m⋅u=M⋅v1+m⋅(v1⋅sin(θ)−e⋅u)⋅sin(θ)
m⋅u=M⋅v1+m⋅v1⋅sin2(θ)−m⋅e⋅u⋅sin(θ)
Rearranging the equation to isolate v1:
m⋅u+m⋅e⋅u⋅sin(θ)=M⋅v1+m⋅v1⋅sin2(θ)
m⋅u(1+e⋅sin(θ))=v1(M+m⋅sin2(θ))
Finally, solving for v1:
v1=m⋅u(1+e⋅sin(θ))M+m⋅sin2(θ)
The velocity of the wedge after the collision is:
v1=m⋅u(1+e⋅sin(θ))M+m⋅sin2(θ)
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Textbook Exercise)
Explore 23 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Additional Exercise)
Explore 7 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Conceptual Questions
Explore 20 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
As shown in the figure, a wedge of mass M is placed on a smooth inclined ramp that makes an angle θ to the horizontal. An object of mass m rests on top of the wedge. The sliding down the ramp at acceleration a. determine the apparent weight of the objects as it slides down. noth that there is friction between the object and the wedge so that the object remains relatively at rest on the wedge.
 AmgcosθBmgcos2θCmgsinθcosθDmgtanθ
AmgcosθBmgcos2θCmgsinθcosθDmgtanθA wedge of height 'h' is released from rest with a light particle P placed on it as shown. The wedge slides down an incline which makes an angle theta with the horizontal. All the surface are smooth, P will reach the surface of the incline in time:
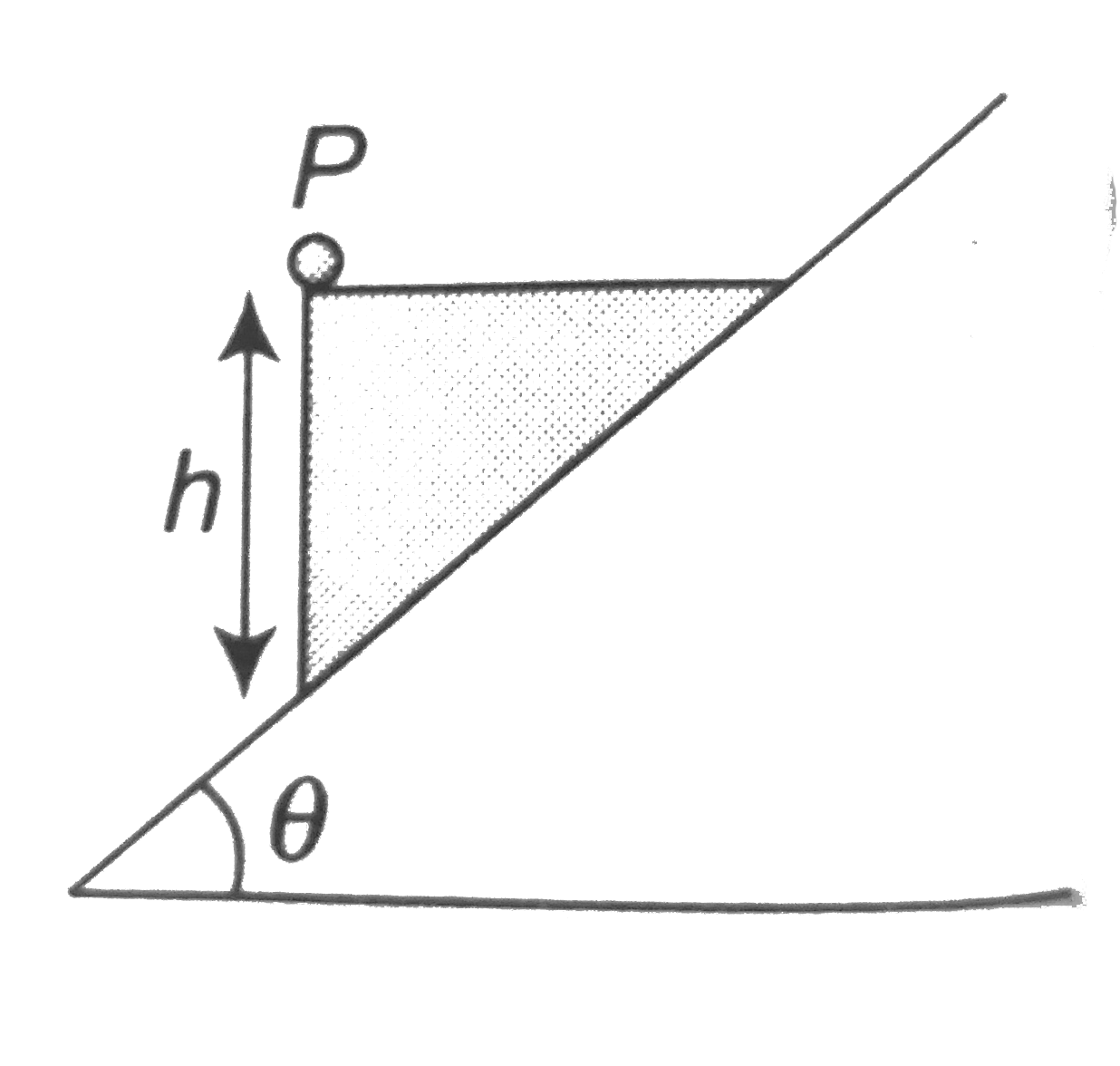 A√2hgsin2θB√2hgsinθcosθC√2hgtanθD√2hgcos2θ
A√2hgsin2θB√2hgsinθcosθC√2hgtanθD√2hgcos2θ
A wedge of mass m1and a block of mass m2are in equlibrium as shown. Inclined surface of the wedge has an inclination α with the horizontal. Each surface is frictionless. The noram reaction on the wedge may be -
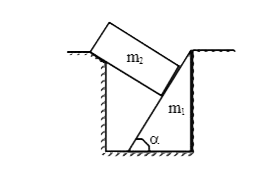
View SolutionA wedge mass m rest on horizontal surface. The inclination of the wedge is α. A ball of mass m moving horizontal with speed u hits the inclined face of the wedge in elastically and after hitting slides up the inclined face of the wedge. Find the velocity of the wedge just after collision. Neglect any friction.
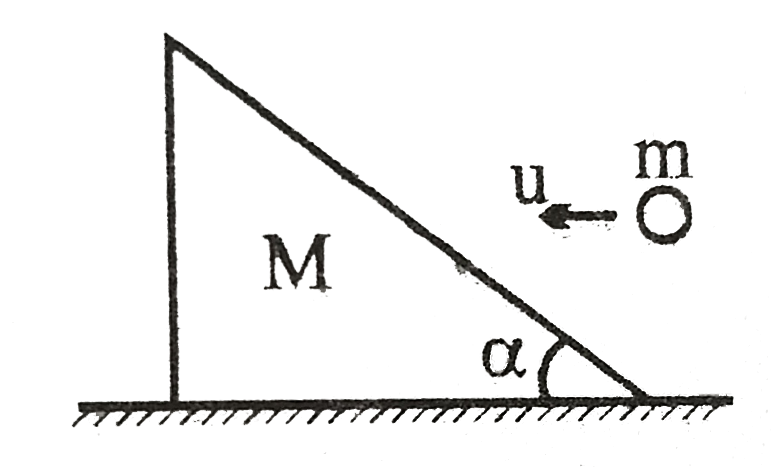
View SolutionA particle of mass m strikes normally to a stationary wedge of mass 5m kept on the smooth horizontal surface as shown.If the particle sticks to the wedge then loss in kinetic energy of the system during collision is?
View SolutionA particle of mass m moving with speed u hits a wedge of mass M as shown in figure. If coefficient of restitution is e and friciton can be neglected, then find the speed of the wedge with respect to ground just after the collision.
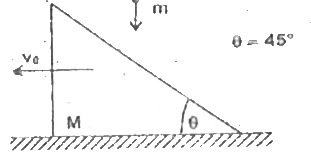
View SolutionA triangular wedge of mass M is moving with uniform velocity v0 along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m.
View SolutionA wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
View Solution

