A uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position if
ω0R>2V0
ω0R=2V0
ω0R<2V0
It is impossible.
The correct Answer is:A

w.r.t. point P net angular momentum must be anticlockwise
mR22ω0>mV0R,ω0R>2V0
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
View SolutionA uniform solid sphere of mass m and radius r = 3m is projected along a rough horizontal surface with the initial velocity v0=6m/s and angular ω0 velocity as shown in the figure. If the sphere finally comes to complete rest then angular velocity is x rad/s. Find x.

View Solution
Knowledge Check
A uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifAω0R=2V0Bω0R<2V0Cω0R>2V0DData insufficientA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
 A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0rA uniform circular disc placed on a horizontal rough surface has initially a velocity v0 and an angular velocity ω0 as shown in the figure. The disc comes to rest after moving some distance in the direction of motion. Then v0/ω0 is :
 Ar/2BrC3r/2D2
Ar/2BrC3r/2D2
A uniform disc of mass m and radius R I rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficnet of friction between te disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA disc of radius R and mass m is projected on to a horizontal floor with a backward spin such that its centre of mass speed is v0 and angular velocity is ω0. What must be the minimum value of ω0 so that the disc eventually returns back?
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is
View SolutionA thin and circular disc of mass m and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . If another disc of same dimension but mass ml4 is placed gently on the first disc co-axially, then the new angular velocity of the system is
View SolutionA uniform circular disc of radius r . 1placed on a rough horizontal plane has initial velocity v0 and an angular velocity ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
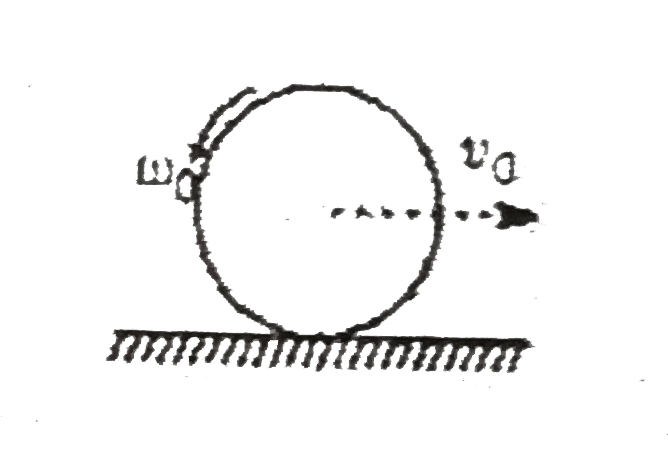
View Solution
