A ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collison with a vertical wall and returns to ground. The total time of flight of the ball is
2vsinθg
2vcosθg
vsin2θg
vcosθg
The correct Answer is:B
To solve the problem of finding the total time of flight of a ball projected from the ground with a velocity V at an angle θ to the vertical, we can follow these steps:
Step 1: Understand the Components of Velocity
When the ball is projected at an angle θ to the vertical, we can resolve the initial velocity V into two components:
- The vertical component Vy=Vcosθ
- The horizontal component Vx=Vsinθ
Step 2: Analyze the Motion
The motion of the ball can be analyzed in two dimensions:
- The vertical motion is influenced by gravity.
- The horizontal motion remains constant since there are no horizontal forces acting on the ball (assuming no air resistance).
Step 3: Time of Flight Calculation
For projectile motion, the time of flight T can be calculated using the formula:
T=2Vyg
where g is the acceleration due to gravity.
Substituting the vertical component of the velocity:
T=2(Vcosθ)g
Step 4: Consider the Collision
Since the ball makes an elastic collision with a vertical wall, the horizontal component of the velocity Vx will reverse direction but maintain its magnitude. However, this does not affect the vertical component of the motion, which is solely responsible for the time of flight.
Step 5: Final Expression for Time of Flight
Thus, the total time of flight remains:
T=2Vcosθg
Conclusion
The total time of flight of the ball is given by:
T=2Vcosθg
---
When the ball is projected at an angle θ to the vertical, we can resolve the initial velocity V into two components:
- The vertical component Vy=Vcosθ
- The horizontal component Vx=Vsinθ
The motion of the ball can be analyzed in two dimensions:
- The vertical motion is influenced by gravity.
- The horizontal motion remains constant since there are no horizontal forces acting on the ball (assuming no air resistance).
For projectile motion, the time of flight T can be calculated using the formula:
T=2Vyg
where g is the acceleration due to gravity.
T=2(Vcosθ)g
Since the ball makes an elastic collision with a vertical wall, the horizontal component of the velocity Vx will reverse direction but maintain its magnitude. However, this does not affect the vertical component of the motion, which is solely responsible for the time of flight.
Thus, the total time of flight remains:
T=2Vcosθg
The total time of flight of the ball is given by:
T=2Vcosθg
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-2 [PARAGRAPH TYPE]
10 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-2 [REASONING TYPE]
10 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
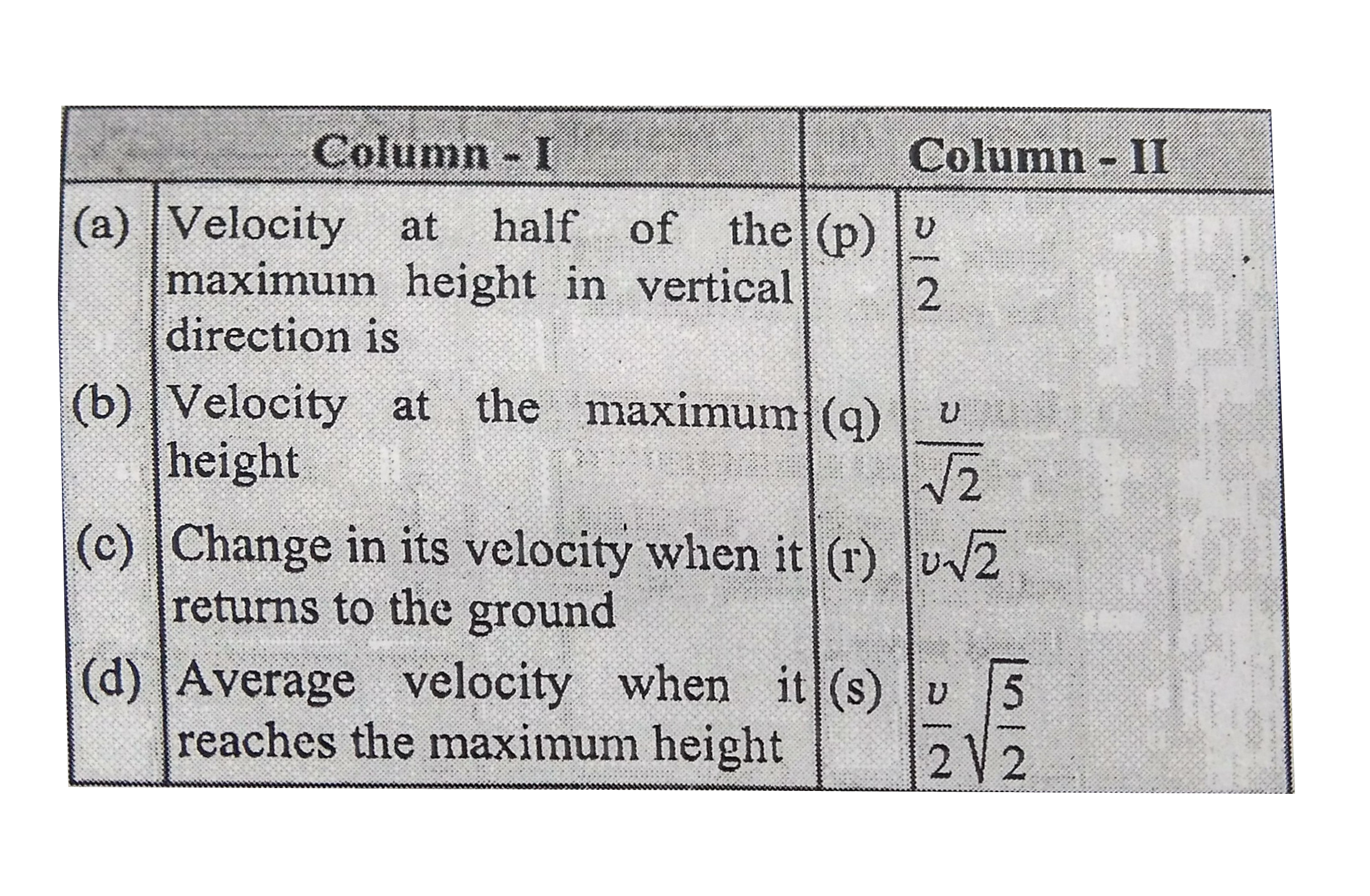
A ball is projected from the ground with velocity v such that its ranege is maximum.
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View Solution
Knowledge Check
A ball is projected from the ground with velocity u such that its range is maximum Then
AIts velocity at half the maximum height is √32uBIts velocity at the maximum height is uCChange in its velocity when it returns to the ground is uDall the above are trueA ball of mass m is projected from the ground with an initial velocity u making an angle of θ with the vertical. What is the change in velocity between the point of projection and the highest point ?
Aucosθ downwardBucosθ upwardCusinθ upwardDusinθ downwardA particle of mass 'm' is projected from ground with velocity u making angle θ with the vertical. The de-Broglie wave length of the particle at the highest point is:
A∞BhmusinθChmucosθDhmu
A particle of mass m is projected form ground with velocity u making angle θ with the vertical. The de Broglie wavelength of the particle at the highest point is
View SolutionA ball is projected from the top of a tower at an angle 60∘ with the vertical. What happens to the vertical component of its velocity?
View SolutionA ball is projected towards right from point A at an angle θ with vertical. A system imparts an acceleration gtanθ to the ball towards left along negative x-axis. The ball will return to ground at :
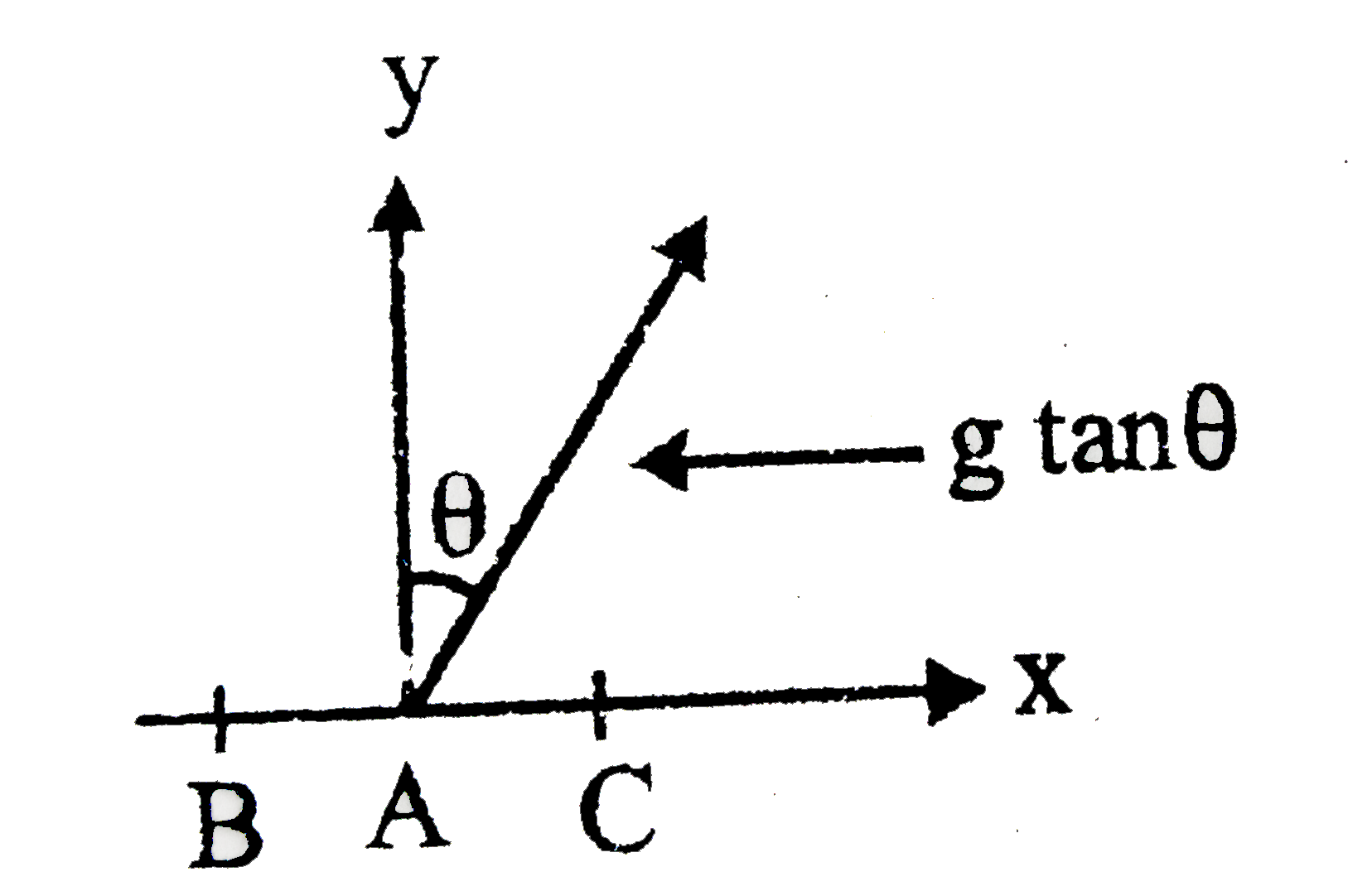
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is

View SolutionA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :

View Solution
