Doubtnut Promotions Sticky

A ball is dropped from a height h. As it bounces off the floor, its speed is 80 percent of what it was just before it hit the floor. The ball will then rise to a height of most nearly

A

0.80h

B

0.75h

C

0.64h

D

0.50h

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

H=v22g∝e2

|
Updated on:21/07/2023
Class 11PHYSICSCENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    A ball is dropped from a height h. As it bounces off the floor, its speed is 80 per cent of what it was just before it hit the floor. The ball will then rise to a height of most nearly:

    A0.80h
    B0.75h
    C0.64h
    D0.50h
  • Question 2 - Select One

    A ball is dropped from a height of 100 m. At the surface of the earth, 20% of its energy is lost. To what height the ball will rise?

    A80m
    B20m
    C40m
    D60m
  • Question 3 - Select One

    A ball is dropped from some height. After rebound from the floor it ascends to the same height. Draw the velocity-time graph for the given motion.

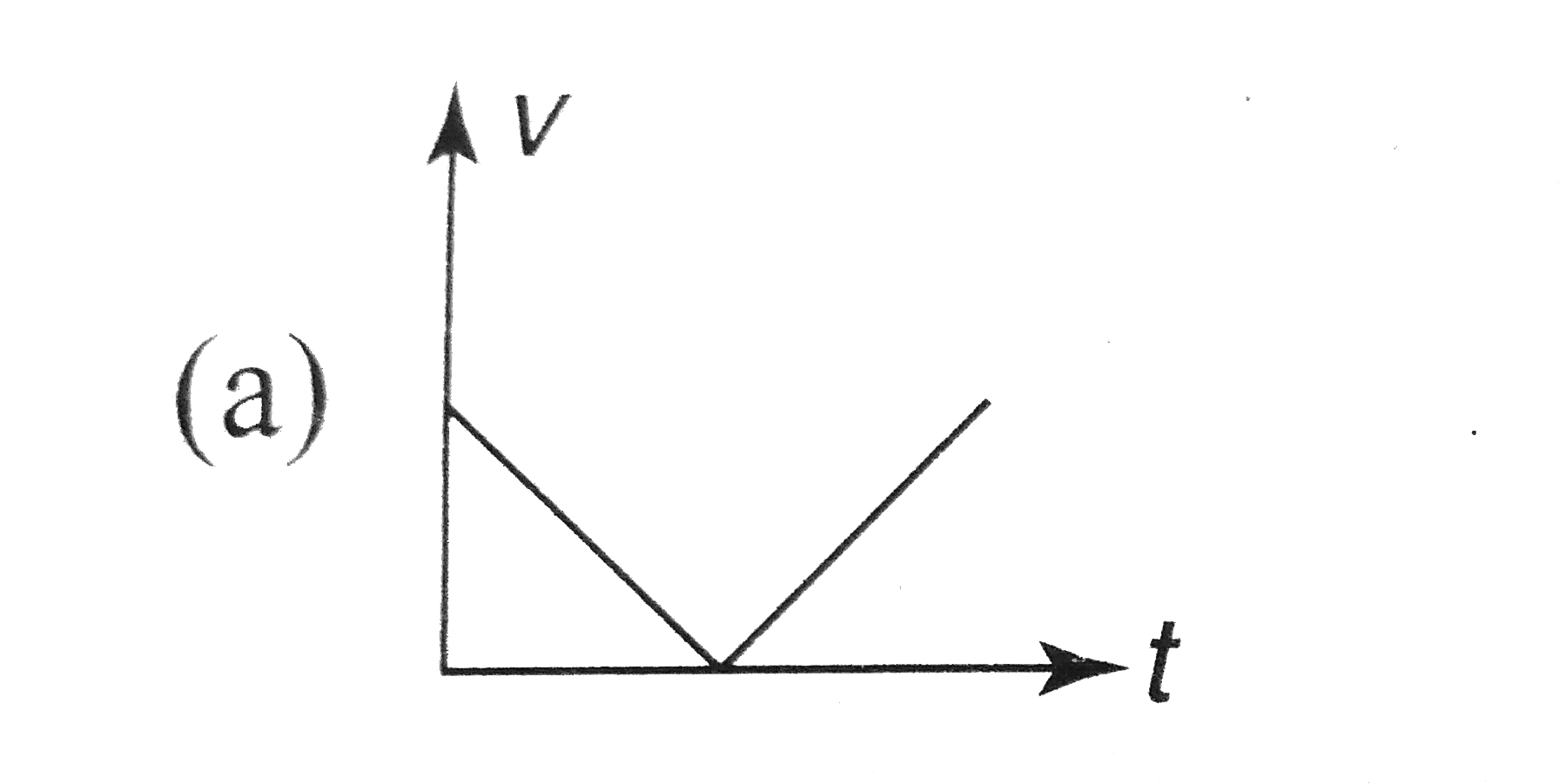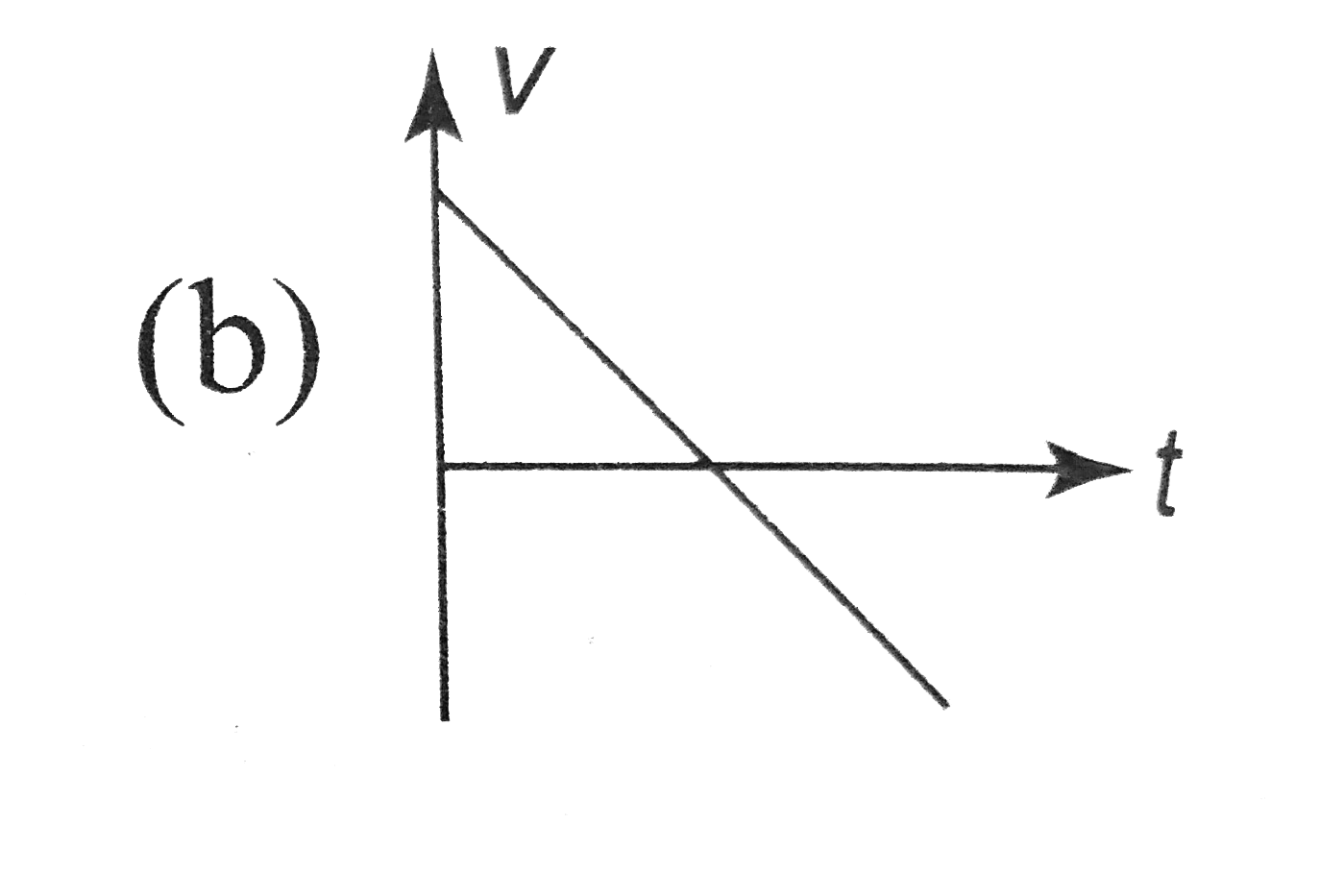    Aocr_image.
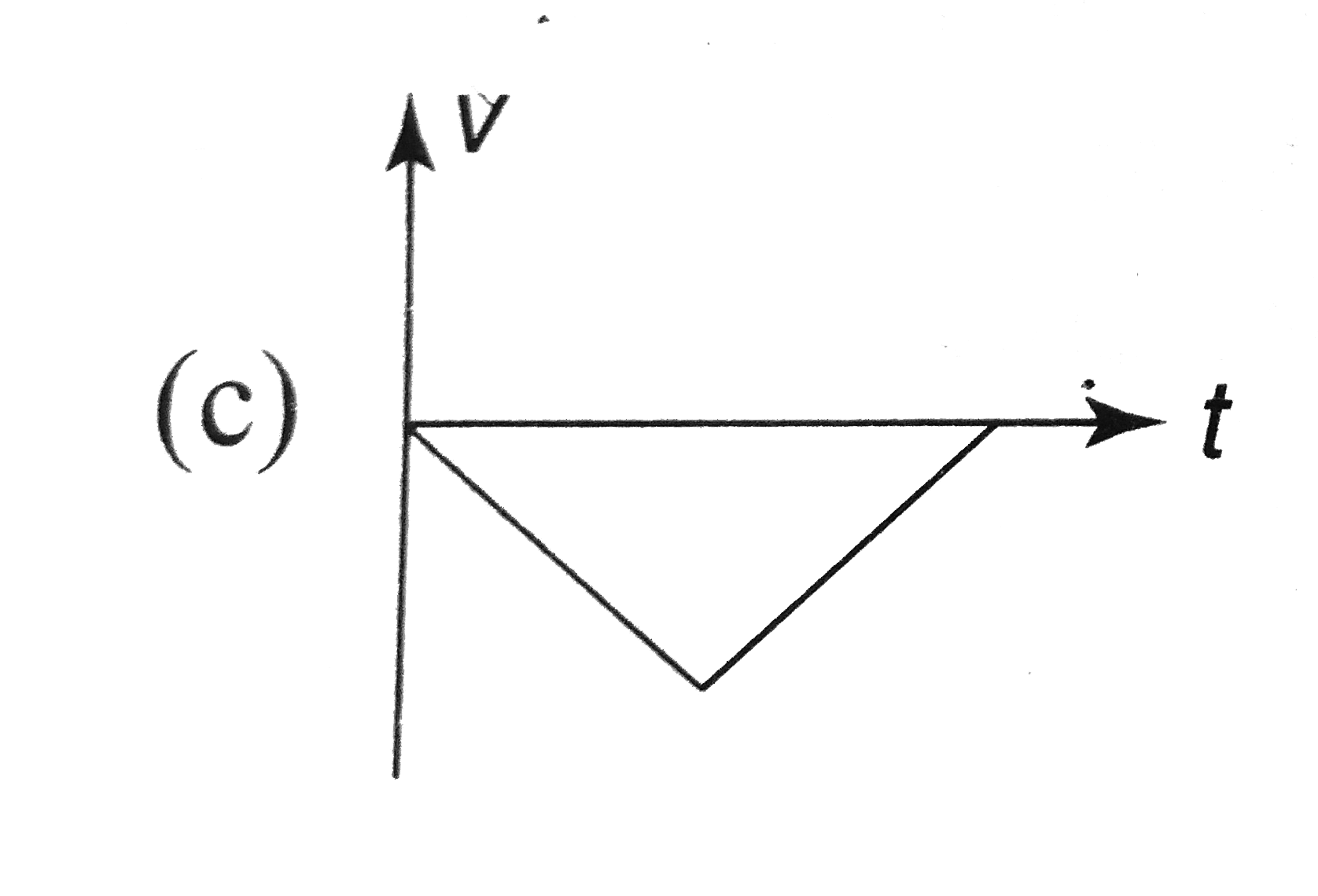    Bocr_image
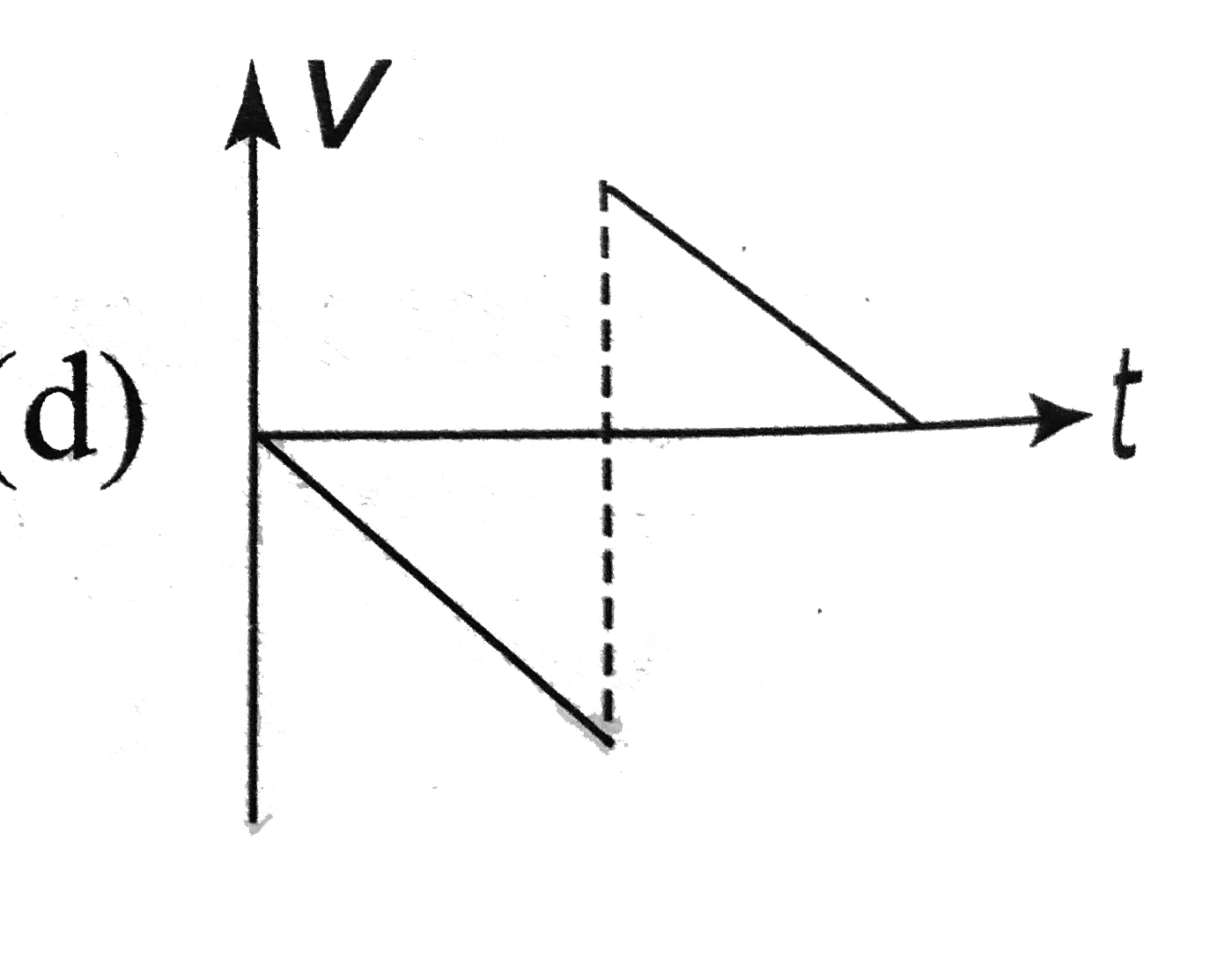    Cocr_image.
    Docr_image.